25考研数据结构复习·1.2.2.1时间复杂度

• 时间复杂度

  • 如何评估算法时间开销？

    事后统计？×

    1. 无法排除与算法本身无关的外界因素
    2. 能否事先估计？eg: 导弹控制算法

• 算法时间复杂度

  事前预估算法时间开销T(n)与问题规模n的关系（T表示“time”）

  eg ： C语言算法实现表白——“爱你n遍”

  //算法1 逐步递增行爱你
  void loveYou(int n){  //n为问题规模
  ①		int i = 1;  //爱你的程度
  ②		while(i <= n){
  ③				i++;  //每次+1
  ④				printf("I Love You %d\\n",i);
  		}
  ⑤		printf("I Love You More Than %d\\n",n);
  }
  
  int main(){
  		loveYou(3000);
  }
  

  语句频度：

  ① 1次

  ② 3001次

  ③④ 3000次

  ⑤ 1次

  T(3000) = 1 + 3001 + 2 * 3000 + 1

  时间开销与问题规模n的关系：T(n) = 3n + 3

?

• 💭问题1：是否可以忽略表达式某些部分？

  结论：可以只考虑阶数高的部分

  🍋大O表示“同阶”，同等数量级。即：当n→∞时，二者之比为常数

  T?(n)=O(n) T?(n)=O(n2) T?(n)=O(n3)

  

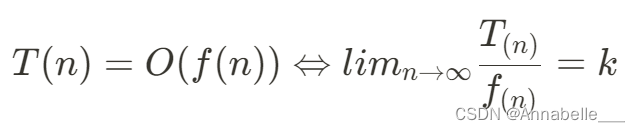
  ！常对幂指阶

  💡 O(1) < O(log?n) < O(n) < O(nlog?n) < O(n2) < O(n3) < O(2?) < O(n!) < O(n?)

?

• 💭问题2：如果有好几千行代码，按这种方法需要一行一行数？

• 结论1：顺序执行的代码智慧影响常数项，可以忽略

  结论2：只需挑循环中的一个基本操作分析它的执行次数与n的关系即可

  结论3：如果有多层嵌套循环，只需要关注最深层循环循环了几次

  //算法2 嵌套循环型爱你
  void loveYou(int n){  //n为问题规模
  ①		int i = 1;  //爱你的程度
      //外层循环执行n次
  ②		while(i <= n){
  ③				i++;  //每次+1
  ④				printf("I Love You %d\\n",i);
  				//内层循环共执行n2次
  				for (int j = 1;j <= n; j++){
  						printf("I am  Iron Man\\n")
  				}  
  		}
  ⑤		printf("I Love You More Than %d\\n",n);
  }
  

  时间开销与问题规模n的关系：T(n) = O(n) + O(n2) = O(n2)

?

//算法3 指数递增型爱你
void loveYou(int n){  //n为问题规模
①		int i = 1;  //爱你的程度
②		while(i <= n){
③				i = i * 2;  //每次翻倍 i=2，4，8，16，32...
④				printf("I Love You %d\\n",i);
		}
⑤		printf("I Love You More Than %d\\n",n);
}

• 计算上述算法的时间复杂度T(n)：

  设最深层循环的语句频度（总共循环的次数）为x(i = 2^x)，则

  由循环条件可知，循环结束时刚好满足2^x > n

  x = log?n + 1

  T(n) = O( log?n)

//算法4 搜索数字型爱你
void loveYou(int flag[], int n){  //n为问题规模
		printf("I Love You %d\\n");
		for(int i = 0;i < n;i++){//从第一个元素开始查找
				if(flag[i] = n){
						printf("I Love You %d\\n",n);
						break;//找到后立即跳出循环
				}
		}
}
//flag数组中乱序存放了1~n这些数
int flag[n] = {1...n};
loveYou(flag,n);

• 计算上述算法的时间复杂度T(n)：

  • 最好情况：元素n在第一个位置：

    最好时间复杂度 T(n) = O(1)

  • 最坏情况：元素n在最后一个位置：

    最坏时间复杂度：T(n) = O(n)

  • 平均情况：假设元素n在任意一个位置的概率相同为1/n（所有输入示例等概率出现）

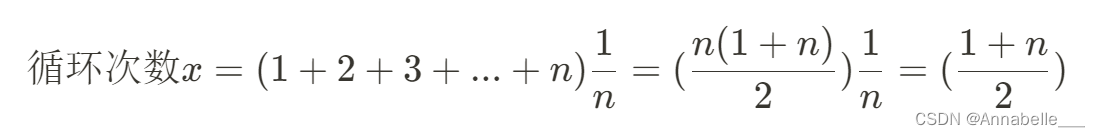?????????????????平均时间复杂度：T(n) = O(n)

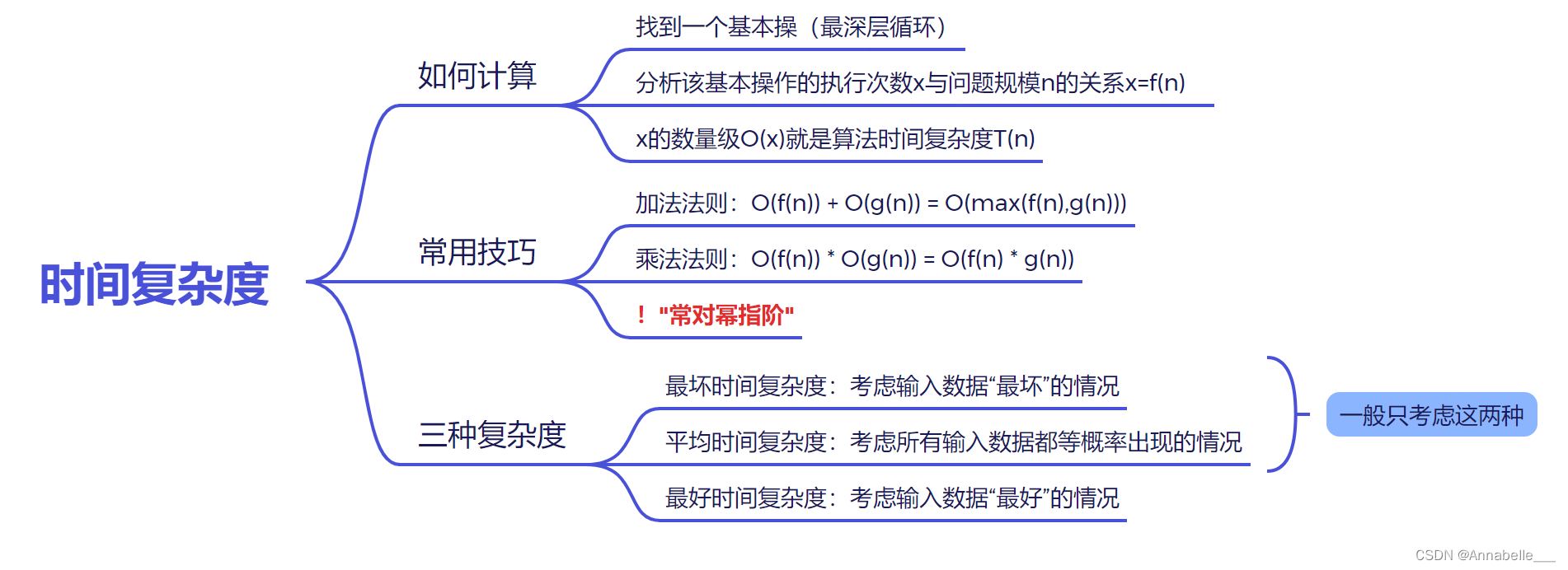
总结?

?

?

?

?