2023.12.26每日一题

LeetCode每日一题

1349.参加考试的最大学生数

1349. 参加考试的最大学生数 - 力扣（LeetCode）

介绍

给你一个 m * n 的矩阵 seats 表示教室中的座位分布。如果座位是坏的（不可用），就用 '#' 表示；否则，用 '.' 表示。

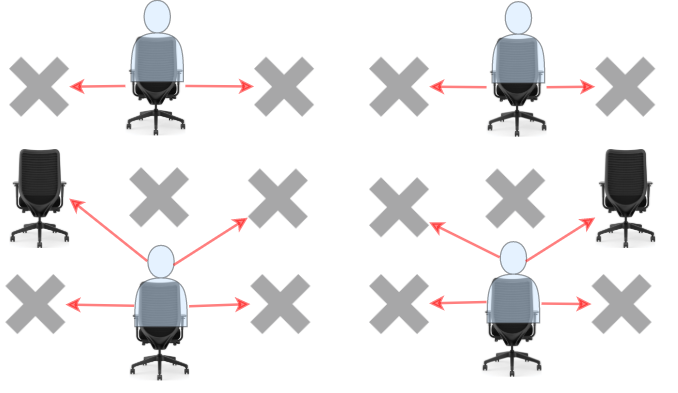
学生可以看到左侧、右侧、左上、右上这四个方向上紧邻他的学生的答卷，但是看不到直接坐在他前面或者后面的学生的答卷。请你计算并返回该考场可以容纳的同时参加考试且无法作弊的 最大 学生人数。

学生必须坐在状况良好的座位上。

示例 1：

输入：seats = [["#",".","#","#",".","#"],
              [".","#","#","#","#","."],
              ["#",".","#","#",".","#"]]
输出：4
解释：教师可以让 4 个学生坐在可用的座位上，这样他们就无法在考试中作弊。 

示例 2：

输入：seats = [[".","#"],
              ["#","#"],
              ["#","."],
              ["#","#"],
              [".","#"]]
输出：3
解释：让所有学生坐在可用的座位上。

示例 3：

输入：seats = [["#",".",".",".","#"],
              [".","#",".","#","."],
              [".",".","#",".","."],
              [".","#",".","#","."],
              ["#",".",".",".","#"]]
输出：10
解释：让学生坐在第 1、3 和 5 列的可用座位上。

提示：

• seats 只包含字符 '.' 和``'#'
• m == seats.length
• n == seats[i].length
• 1 <= m <= 8
• 1 <= n <= 8

思路

没有思路，这题目对目前的我来说太难了，直接使用cv大法

下面是我在LeetCode看到的思路

dfs(i, j)：在第 i 排的座位状态为 j 的情况下，前 i 排的最大学生数 对于当前第 i 排，有两种大致情况： （1）第 i 排空着 （2）第 i 排坐人 对于情况（2）如果i不为第一排，则需要枚举每一种可能的情况，从而计算。 如果是第一排，则此时直接算出最多能坐的数量即可。根据贪心，从左到右依次选出最低位的1坐人，并且将其相邻的bit及其本身置0，表示不可再坐人（相邻座位同时坐人会抄答案）

作者：爱吃鱼的猫
链接：https://leetcode.cn/problems/maximum-students-taking-exam/ 来源：力扣（LeetCode） 著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

代码

C++

class Solution {
public:
    int maxStudents(vector<vector<char>>& seats) {
        int m = seats.size(), n = seats[0].size();
        vector<int> a(m); // a[i] 是第 i 排客用椅子的下标集合
        for(int i = 0; i < m; i++){
            for(int j = 0; j < n; j++){
                if(seats[i][j] == '.'){
                    a[i] |= 1 << j; // 用 1 表示该位置可坐
                }
            }
        }

        vector<vector<int>> memo(m, vector<int>(1 << n, -1)); // 初始化为 -1 表示未计算
        function<int(int, int)> dfs = [&](int i, int j) -> int{
            int &res = memo[i][j]; // 注意是引用
            if(res != -1){
                return res;
            }
            if(i == 0){
                if(j == 0) return res = 0;
                int lb = j & -j;
                return res = dfs(i, j & ~(lb * 3)) + 1;
            }
            res = dfs(i - 1, a[i - 1]); // 第 i 排空着
            for(int s = j; s; s = (s - 1) & j){ // 枚举 j 的子集 s
                if((s & (s >> 1)) == 0){ // s 没有连续的 1 (如果有连续的1即相邻座位同时坐人，不符合要求)
                    int t = a[i - 1] & ~(s << 1 | s >> 1); // 上一排不能坐人的位置
                    res = max(res, dfs(i - 1, t) + __builtin_popcount(s));
                }
            }
            return res;
        };
        return dfs(m - 1, a[m - 1]);
    }
};