LeetCode---120双周赛
题目列表
一、统计移除递增子数组的数目I

这题的数据范围不高,可以直接暴力,后面的第三题和它一样,但是数据范围增强,这里先写一种暴力的解法,后面第三题在讲个O(n)的解法
class Solution {
public:
int incremovableSubarrayCount(vector<int>& nums) {
int n=nums.size();
int ans=0;
//枚举删除的子数组的左右断点[i,j]
for(int i=0;i<n;i++){
for(int j=i;j<n;j++){
bool flag=true;
vector<int>v(nums.begin(),nums.begin()+i);
v.insert(v.end(),nums.begin()+j+1,nums.end());
for(int k=0;k<v.size();k++){
if(k&&v[k]<=v[k-1]){
flag=false;
break;
}
}
ans+=flag;
}
}
return ans;
}
};二、找到最大周长的多边形
这题的难度不高,题目意思说的很明确,我们只要照着模拟就行,用贪心的思想:因为多边形的周长要最长,我们肯定是先考虑全选的情况,然后看是否符合多边形的条件,如果不符合,我们只能将最长的边换小一点,同时比最长边小的边全部选上,这样不等式左边的数的和才会尽可能的大,会更有可能满足多边形的条件
代码如下
class Solution {
public:
long long largestPerimeter(vector<int>& nums) {
int n=nums.size();
sort(nums.begin(),nums.end());
long long sum=accumulate(nums.begin(),nums.end(),0LL);
for(int i=n-1;i>1;i--){//多边形最少要三条边
if(sum-nums[i]>nums[i])
return sum;
sum-=nums[i];
}
return -1;
}
};三、移除递增子数组的数目II
第一题的数据加强版,第一题我们是纯模拟,时间复杂度为O(n^3),很显然过不了,所以我们要观察它给的示例,来找找规律
上面只截取了示例1,是一个特殊情况,当数组本身就是递增的情况下,答案就是数组能产生多少个子数组,为(n+1)*n/2
那么如果数组不严格单调增呢?
我们可以将子数组分为三种:
1、右端点固定在数组最右边,看前缀的递增数组能到哪里
2、左端点固定在数组最左边,看后缀的递增数组能到哪里
3、子数组在数组的中间
前面两种情况很好解决,第三种情况怎么求?
首先我们要明确一点,由于我们是在中间找子数组,所以数组的前缀和后缀一定要是递增的,我们只要看前缀的最后一个数是否比后缀的第一个数大就行。
同时为了得到子数组的数量和降低时间复杂度,我们可以用双指针(同向双指针),这里用到前缀/后缀数组的单调性,可以简单说明一下该算法的步骤和正确性
设i为a数组的下标,j为b数组的下标,都从前往后移动,两个数组同时满足单调增
- 如果a[i]<b[j],根据单调性,j后面的数字一定也满足小于关系,所以直接加上后面的数字个数,同时i++,看看a数组的下一个数字是否也小于b[j]
- 如果a[i]>=b[j],根据单调性,j前面的数字也一定满足大于等于关系,所以直接让j++
总而言之,我们在遍历a数组的同时,让b数组中的数始终被划分为可能满足条件和永远不可能满足条件两个部分,时间复杂度的降低本质在于永远不能满足条件的部分不会被重复的遍历到
代码如下
class Solution {
public:
long long incremovableSubarrayCount(vector<int>& nums) {
int n=nums.size();
//找前缀递增的最后一个元素下标
int i=0;
while(i<n-1){
if(nums[i]>=nums[i+1])
break;
i++;
}
if(i==n-1) return 1LL*n*(n+1)/2;
//找后缀递增的第一个元素下标
int j=n-1;
while(j>0){
if(nums[j-1]>=nums[j])
break;
j--;
}
//要考虑将整个数组变成空数组的情况,所以单独+1
long long ans=(n - j) + (i + 1) + 1;
int l=0,r=j;
while(l<=i&&r<n){
if(nums[l]<nums[r]){
ans+=(n-r);
l++;
}else{
r++;
}
}
return ans;
}
};(当然,双指针同时从后往前遍历也是可以的,这样可以将找递增后缀和双指针结合起来写,有兴趣的读者可以回去试着去改改代码)?
四、树中每个节点放置的金币数目
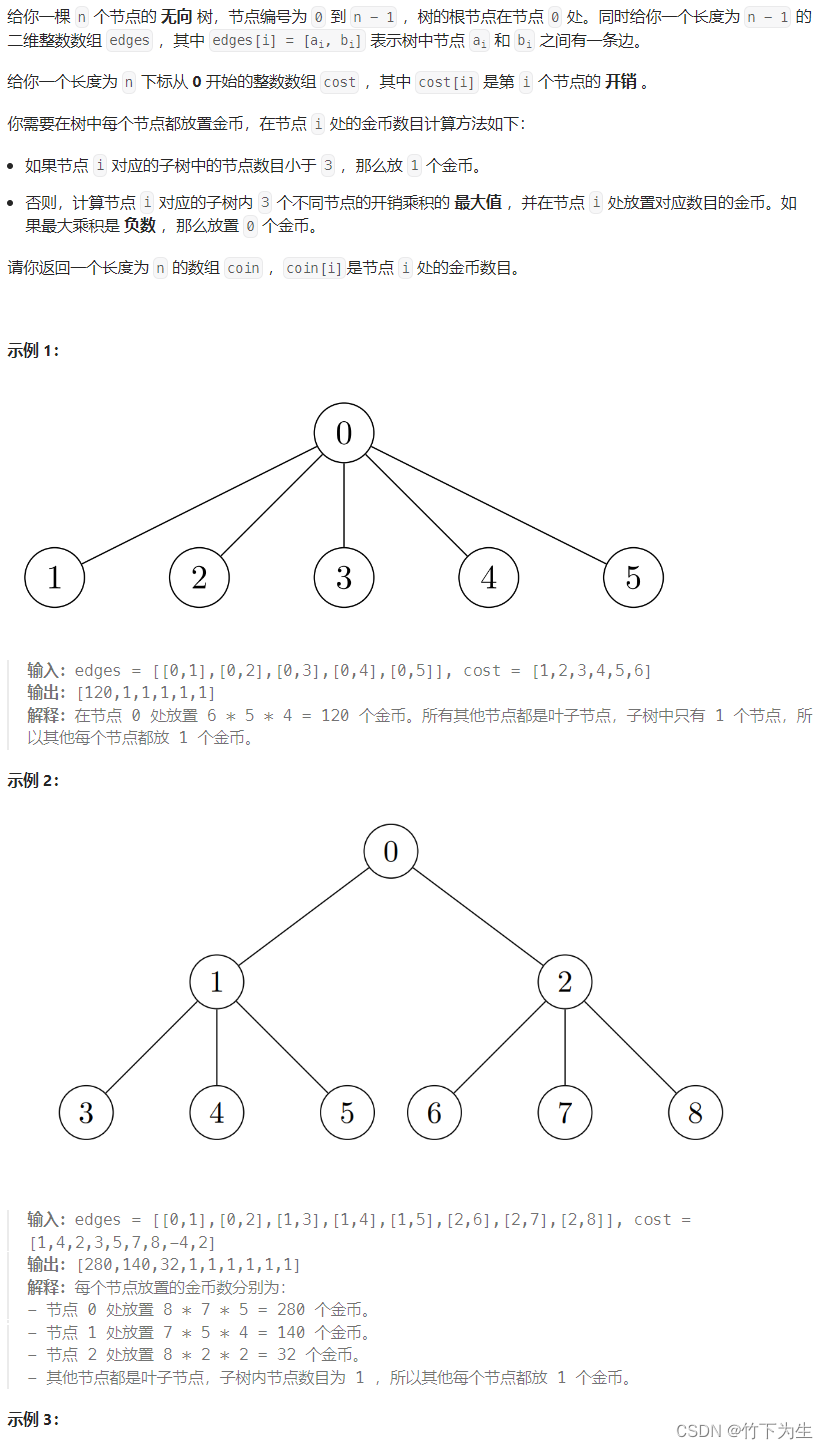
这题说实在的没有什么难点,关键是你要知道如何建图和遍历这棵树。
还有一个比较关键的点简单说明一下:当子树中的结点个数>=3时,我们如何选取3个数字使得它们的乘积最大?这其实很好思考,我们只要将数组排序,因为题目要求小于0,就放置0个金币,所以我们只要考虑选三个数字,它们的乘积为最大的正整数即可,
两种可能性:
- 三个数都为正,选择最大的三个数
- 三个数中两个数为负,选最小的两个数,一个数为正,选一个最大的数
至于这两种情况中是否会出现三个数全为负数的情况,我们根本不用管,因为题目要求小于0,就放置0个金币。
有人可能也是这样写的,但是超时了没过,这里讲一下为什么,因为数组太大了,排序需要时间,但其实我们没必要将子树的所有cost都排序,我们只想知道这些数字中最小的两个数和最大的三个数(当然要考虑到重合的情况,因为我们不能凭空多出数字)。
代码如下
class Solution {
public:
vector<long long> placedCoins(vector<vector<int>>& edges, vector<int>& cost) {
int n=cost.size();
vector<long long>ans(n);
vector<vector<int>>g(n);
for(auto&e:edges){
int x=e[0],y=e[1];
g[x].push_back(y);
g[y].push_back(x);
}
function<vector<long long>(int,int)>dfs=[&](int x,int fa)->vector<long long>{
vector<long long>v({cost[x]});
for(int y:g[x]){
if(y!=fa){
vector<long long>w=dfs(y,x);
v.insert(v.end(),w.begin(),w.end());
}
}
int m=v.size();
if(m<3)
ans[x]=1;
else{
sort(v.begin(),v.end());
long long a=v[m-1]*v[m-2]*v[m-3];
long long b=v[0]*v[1]*v.back();
ans[x]=max(max(a,b),0LL);
}
if(m>5){
v.erase(v.begin()+2,v.end()-3);
}
return v;
};
dfs(0,-1);
return ans;
}
};本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!

