【LeetCode 热题 HOT 100】题解笔记 —— Day04
? 作者主页:欢迎来到我的技术博客😎
? 个人介绍:大家好,本人热衷于Java后端开发,欢迎来交流学习哦!( ̄▽ ̄)~*
🍊 如果文章对您有帮助,记得关注、点赞、收藏、评论??????
📣 您的支持将是我创作的动力,让我们一起加油进步吧!!!🎉🎉
文章目录
一、颜色分类
1. 题目描述

2. 思路分析
这道题的思路很难可以想到。
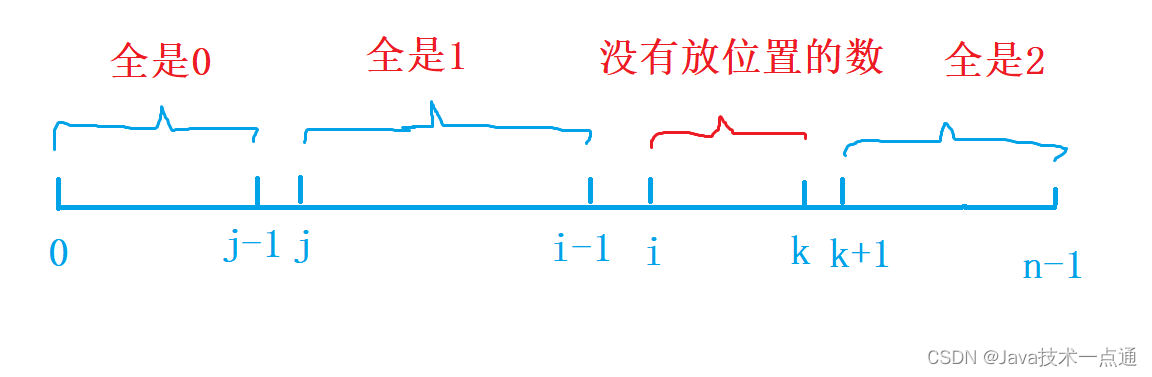
如图所示,
[
0
,
j
?
1
]
[0,j - 1]
[0,j?1] 维护的是全是
0
0
0 的区间,
[
j
,
i
?
1
]
[j,i - 1]
[j,i?1] 维护的是全是
1
1
1 的区间,
[
k
+
1
,
n
?
1
]
[k + 1,n - 1]
[k+1,n?1] 维护的是全是
2
2
2 的区间,而
[
i
,
k
]
[i,k]
[i,k] 区间的元素是还没放的数。
枚举整个数组,若当前枚举到的位置是 i i i:
- 若
nums[i] == 0,则交换 i i i 和 j j j 的位置的元素,由于nums[i] == 0且nums[j] == 1,因此交换后 i i i 和 j j j 同时往后移动1位; - 若
nums[i] == 1,则直接i ++; - 若
nums[i] == 2,则交换 i i i 和 k k k 位置的元素,由于nums[i] == 2,因此填入到 k k k 位置时, k k k 的元素就是2,因此 k k k 需要往前移动1位,而交换过来可能是2 也可能是0 而i的元素未知,不做移动。
3. 代码实现
class Solution {
public:
void sortColors(vector<int>& nums) {
for (int i = 0, j = 0, k = nums.size() - 1; i <= k;) {
if (nums[i] == 0) swap(nums[i ++], nums[j ++]);
else if (nums[i] == 2) swap(nums[i], nums[k --]);
else i ++;
}
}
};
二、最小覆盖子串
1. 题目描述

2. 思路分析
三、子集
1. 题目描述
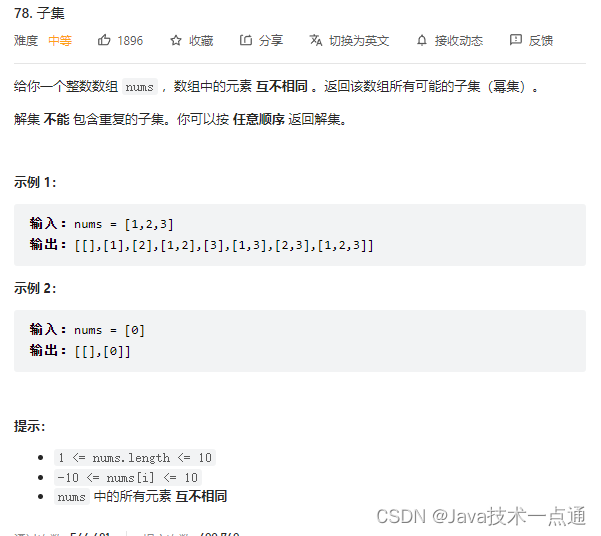
2. 思路分析
dfs
和全排列的做法一样,当我们走到叶子结点时,就把该路径加入方案中。如果还没有走到叶子节点,那么对于枚举的当前数,我们有两种选择,选或不选,做出选择再递归到下一层,同时记得回溯。
3. 代码实现
class Solution {
public:
vector<vector<int>> res;
vector<int> path;
vector<vector<int>> subsets(vector<int>& nums) {
dfs(nums, 0);
return res;
}
void dfs(vector<int> nums, int u) {
if (u >= nums.size()) {
res.push_back(path);
return;
}
dfs(nums, u + 1); // 不选当前数,递归下一层
path.push_back(nums[u]); // 选当前数
dfs(nums, u + 1); // 递归
path.pop_back(); // 回溯
}
};
四、单词搜索
1. 题目描述
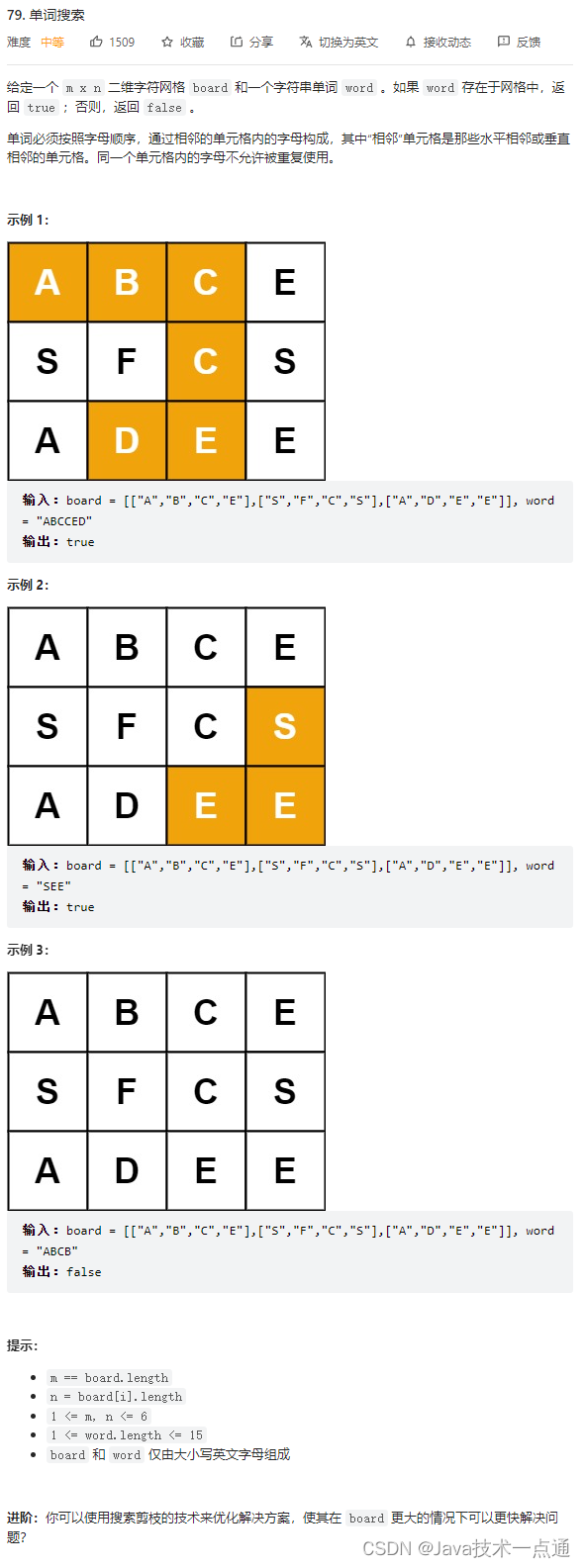
2. 思路分析
(dfs)
在深度优先搜索中,最重要的就是考虑好搜索顺序。
我们先枚举单词的起点,然后依次枚举单词的每个字母。
过程中需要将已经使用过的字母改成一个特殊字母,以避免重复使用字符。
3. 代码实现
class Solution {
public:
bool exist(vector<vector<char>>& board, string word) {
for (int i = 0; i < board.size(); i ++) {
for (int j = 0; j< board[i].size(); j ++) {
if (dfs(board, word, 0, i, j)) return true;
}
}
return false;
}
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
bool dfs(vector<vector<char>>& board, string& word, int u, int x, int y) {
if (board[x][y] != word[u]) return false;
if (u == word.size() - 1) return true;
char t = board[x][y];
board[x][y] = '.';
for ( int i = 0; i < 4; i ++) {
int a = x + dx[i], b = y + dy[i];
if (a < 0 || a >= board.size() || b < 0 || b >= board[0].size() || board[a][b] == '.') continue;
if (dfs(board, word, u + 1, a, b)) return true;
}
board[x][y] = t;
return false;
}
};
五、柱状图中最大的矩形
1. 题目描述
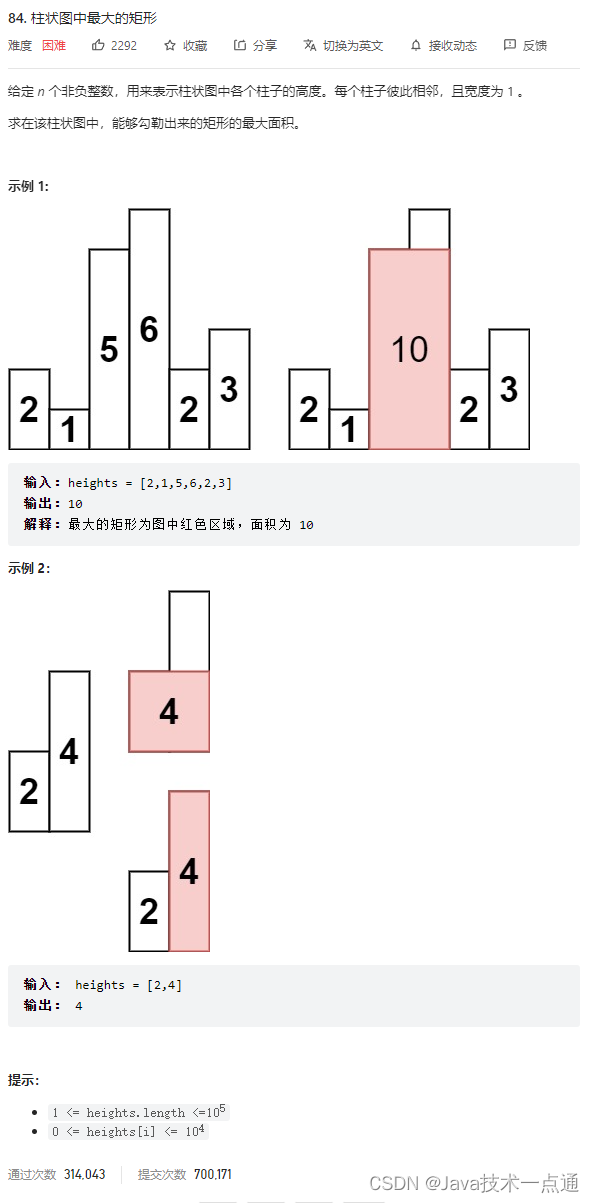
2. 思路分析
单调栈
- 此题的本质是找到每个柱形条左边和右边最近的比自己低的矩形条,然后用宽度乘上当前柱形条的高度作为备选答案。
- 解决此类问题的经典做法是单调栈,维护一个单调递增的栈,如果当前柱形条 i i i 的高度比栈顶要低,则栈顶元素 c u r cur cur 出栈。出栈后, c u r cur cur 右边第一个比它低的柱形条就是 i,左边第一个比它低的柱形条是当前栈中的 t o p top top。不断出栈直到栈为空或者柱形条 i i i 不再比 t o p top top 低。
- 满足 操作2 之后,当前矩形条 i i i 进栈。
3. 代码实现
class Solution {
public:
int largestRectangleArea(vector<int>& h) {
int n = h.size();
vector<int> left(n), right(n);
stack<int> stk;
for (int i = 0; i < n; i ++) {
while (stk.size() && h[stk.top()] >= h[i]) stk.pop();
if (stk.empty()) left[i] = -1;
else left[i] = stk.top();
stk.push(i);
}
stk = stack<int>();
for (int i = n - 1; i >= 0; i --) {
while (stk.size() && h[stk.top()] >= h[i]) stk.pop();
if (stk.empty()) right[i] = n;
else right[i] = stk.top();
stk.push(i);
}
int res = 0;
for (int i = 0; i < n; i ++) {
res = max(res, h[i] * (right[i] - left[i] - 1));
}
return res;
}
};
六、最大矩阵
七、二叉树的中序遍历
1. 题目描述

2. 思路分析
递归算法比较简单,就根据中序遍历的过程,先遍历左子树,再遍历当前根,然后遍历右子树。递归函数的中止条件是当前结点为空,同时当遍历当前结点时,将该点加入遍历数组即可。
3. 代码实现
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<int> res;
vector<int> inorderTraversal(TreeNode* root) {
dfs(root);
return res;
}
void dfs(TreeNode* root) {
if (!root) return;
dfs(root->left);
res.push_back(root->val);
dfs(root->right);
}
};
八、不同的二叉搜索树
1. 题目描述
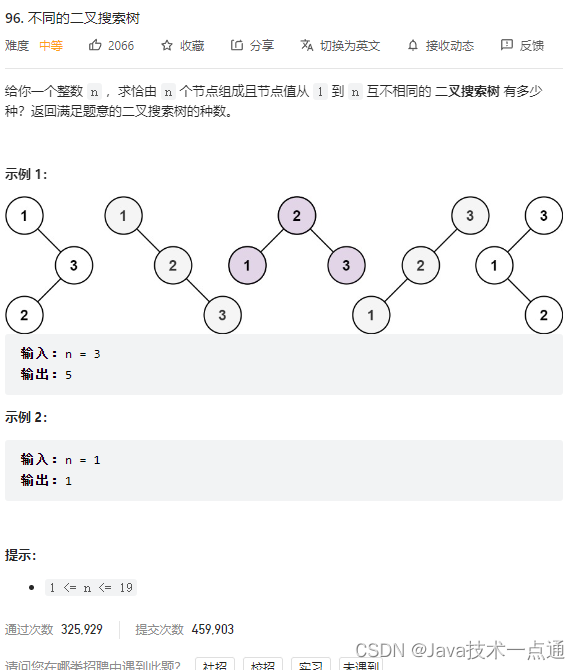
2. 思路分析
(动态规划)
对于
n
n
n 个节点的 BST,除去根节点有
n
?
1
n - 1
n?1 个节点,将这
n
?
1
n - 1
n?1 个节点分配在根节点的两侧,即可构造出所有的方案。
状态表示:
f
[
n
]
f[n]
f[n] 表示
n
n
n 个节点的二叉搜索树共有多少种。
状态转移: 左子树可以有
0
,
1
,
.
.
.
,
n
?
1
0,1,...,n - 1
0,1,...,n?1 个节点,对应的右子树有
n
?
1
,
n
?
2
,
.
.
.
,
0
n - 1, n - 2, ..., 0
n?1,n?2,...,0 个节点,
f
[
n
]
f[n]
f[n] 是所有这些情况的总和,即
f
[
n
]
=
f
[
0
]
?
f
[
n
?
1
]
+
f
[
1
]
?
f
[
n
?
2
]
+
…
+
f
[
n
?
1
]
?
f
[
0
]
f[n]=f[0]?f[n?1]+f[1]?f[n?2]+…+f[n?1]?f[0]
f[n]=f[0]?f[n?1]+f[1]?f[n?2]+…+f[n?1]?f[0]
3. 代码实现
class Solution {
public:
int numTrees(int n) {
vector<int> f(n + 1);
f[0] = 1;
for (int i = 1; i <= n; i ++)
for (int j = 1; j <= i; j ++)
f[i] += f[j - 1] * f[i - j];
return f[n];
}
};
九、验证二叉搜索树
1. 题目描述
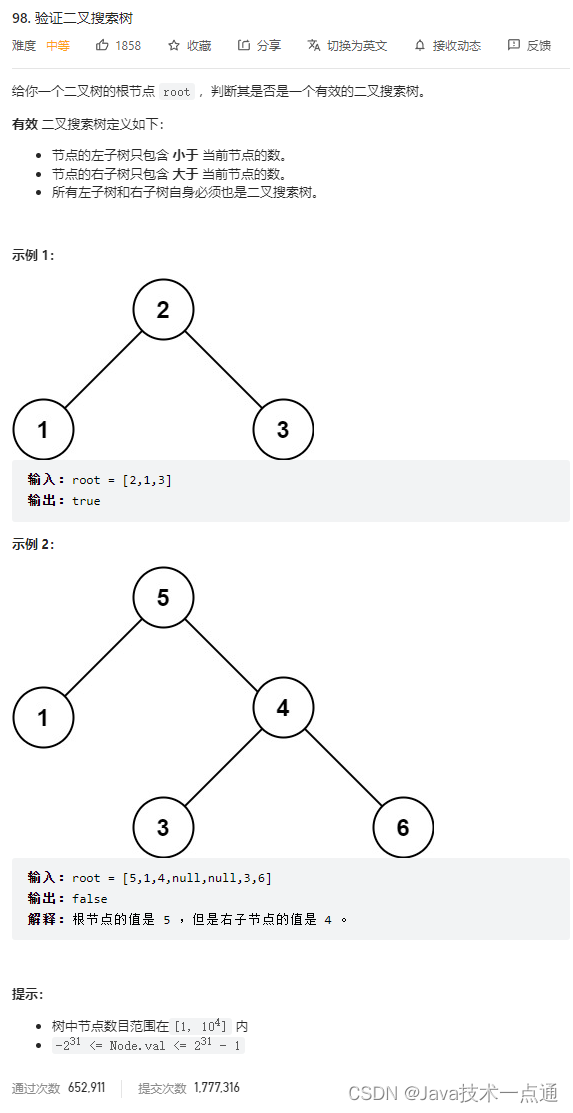
2. 思路分析
(深度优先遍历)
深度优先遍历整棵子树。
遍历时,需要向上传递当前子树中的最小值和最大值,这里可以用C++中的引用来专递。
对于当前节点,我们先遍历它的左子树,判断左子树是否合法,同时判断左子树的最大值是否小于当前节点的值;然后遍历右子树,判断右子树是否合法,同时判断右子树的最小值是否大于当前节点的值。
如果条件均满足,说明以当前节点为根的子树是一棵合法的二叉搜索树,返回
t
r
u
e
true
true。
3. 代码实现
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
bool isValidBST(TreeNode* root) {
if (!root) return true;
int maxv, minv;
return dfs(root, maxv, minv);
}
bool dfs(TreeNode* root, int &maxv, int &minv) {
maxv = minv = root->val;
if (root->left) {
int nowMaxv, nowMinv;
if (!dfs(root->left, nowMaxv, nowMinv))
return false;
if (nowMaxv >= root->val)
return false;
maxv = max(maxv, nowMaxv);
minv = min(minv, nowMinv);
}
if (root->right) {
int nowMaxv, nowMinv;
if (!dfs(root->right, nowMaxv, nowMinv))
return false;
if (nowMinv <= root->val)
return false;
maxv = max(maxv, nowMaxv);
minv = min(minv, nowMinv);
}
return true;
}
};
十、对称二叉树
1. 题目描述
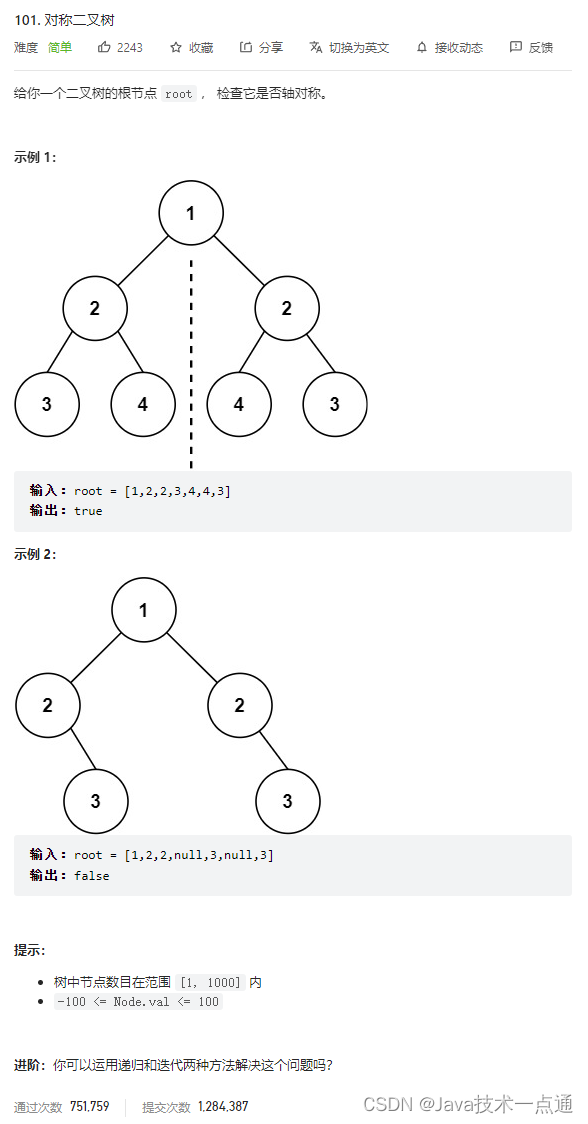
2. 思路分析
递归判断两个子树是否互为镜像。
两个子树互为镜像当且仅当:
- 两个子树的根节点值相等;
- 第一棵子树的左子树和第二棵子树的右子树互为镜像,且第一棵子树的右子树和第二棵子树的左子树互为镜像;
3. 代码实现
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
bool isSymmetric(TreeNode* root) {
if (!root) return true;
return dfs(root->left, root->right);
}
bool dfs(TreeNode* p, TreeNode* q) {
if (!p && !q) return true;
if (!p || !q || p->val != q->val) return false;
return dfs(p->left, q->right) && dfs(p->right, q->left);
}
};
?
非常感谢您阅读到这里,如果这篇文章对您有帮助,希望能留下您的点赞👍 关注💖 分享👥 留言💬thanks!!!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- Blazor + SqlSugar 实现单表增删改功能
- 基于SSM的高校竞赛和考级查询系统【数据库设计、论文、毕设源码、开题报告】
- 交互式博客
- 4-Docker命令之docker logout
- C++关联容器概念,相关操作和代码示例
- 【TypeScript】声明文件
- FPGA模块——以太网芯片MDIO读写
- cuda10.2安装python3.7pytorch
- ffmpeg 安装
- 【Mode Management】ComM详细介绍