代码随想录算法训练营Day12 | 102.二叉树的层序遍历、226.翻转二叉树、101.对称二叉树
发布时间:2023年12月28日
LeetCode 102 二叉树的层序遍历
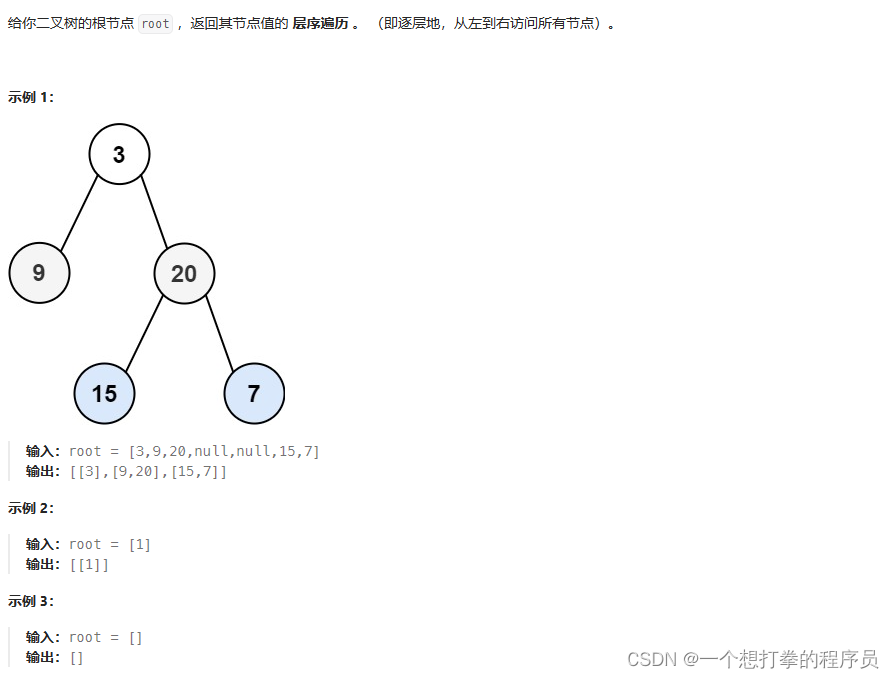
本题思路:本题要求我们,按一层一层的顺序,保存每一层的元素。所以我们借助队列来实现。
- 需要定义一个 size,来记录每一层的元素数量,这是关键点
- 然后根据每一层的元素个数,循环弹出,如果有左右孩子就加入到队列中。并记录下来弹出的元素
- 这样弹出某一层的所有元素后,下一层的所有元素就存进去队列了。
- 然后依次重复上述步骤即可。直到队列为空
class Solution {
public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> res = new LinkedList();
Deque<TreeNode> deque = new ArrayDeque<>();
// 从尾入队
if(root == null){
return res;
}
deque.offer(root);
while (!deque.isEmpty()){
// 记录当前size 大小,表示当前层元素节点个数
int size = deque.size();
// 存储每一层元素
List<Integer> list = new LinkedList<>();
for (int i = 0; i < size; i++) {
TreeNode cur = deque.poll();
if (cur.left != null){
deque.offer(cur.left);
}
if (cur.right != null){
deque.offer(cur.right);
}
list.add(cur.val);
}
// 将该层元素添加到 res 中
res.add(list);
}
return res;
}
}
LeetCode 223 翻转二叉树
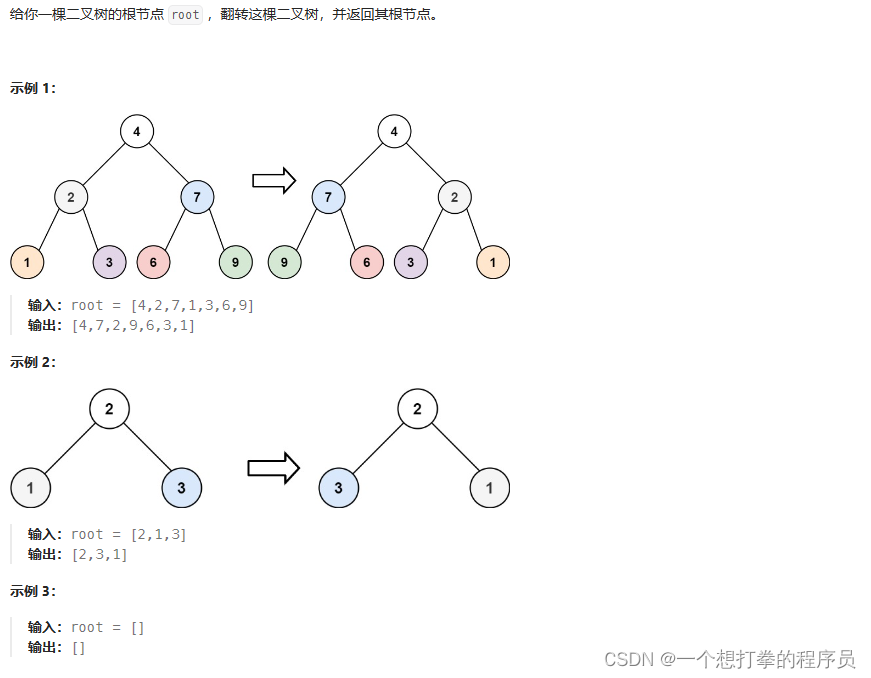
本题思路:利用递归来完成,但是很多人写过一遍以后,可能下次又忘记了怎么写。因为不知道到底用的是前序遍历,还是后序遍历,又或者中序遍历。
- 我们先讲解下前序遍历的情况。前序遍历的顺序是: 根 左 右。
- 那就是首先以根中心,翻转它的左右孩子
- 然后又以左孩子为根节点,翻转它的左右节点
- 最后以右孩子为根节点,翻转它的左右孩子
那么代码就很好写
class Solution {
public TreeNode invertTree(TreeNode root) {
if(root == null){
return root;
}
// 先交换左右节点
TreeNode tmp = root.left;
root.left = root.right;
root.right = tmp;
invertTree(root.left);
invertTree(root.right);
return root;
}
}
后序遍历的话,只要移动下代码位置即可。
class Solution {
public TreeNode invertTree(TreeNode root) {
if(root == null){
return root;
}
invertTree(root.left);
invertTree(root.right);
TreeNode tmp = root.left;
root.left = root.right;
root.right = tmp;
return root;
}
}
LeetCode 101 对称二叉树
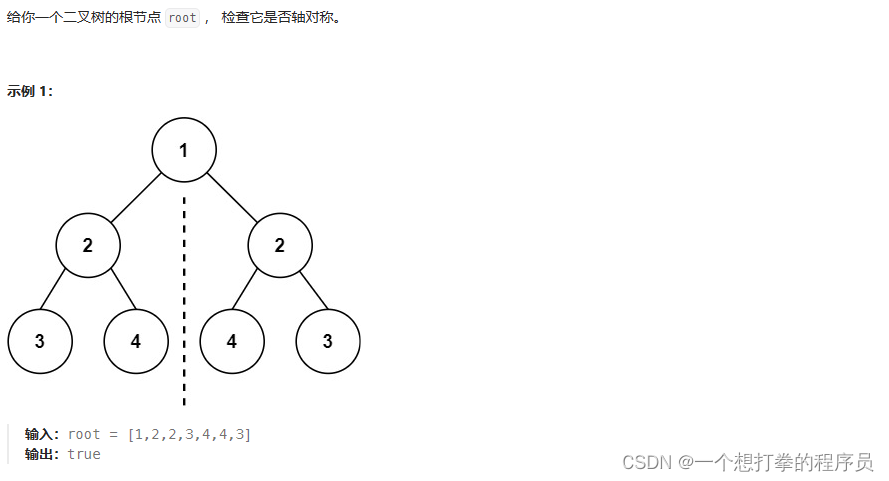
本题思路:既然是判断是否是对称二叉树,那么我们肯定是比较外侧节点是否对称,然后比较内侧节点是否对称,如果都对称,则这个树是对称二叉树。
所以我们采用递归的方法。递归的第一步就是先找出口
- 左孩子为空,右孩子为空,则返回 true
- 左孩子不空,右孩子为空,则返回 false
- 左孩子为空,右孩子不空,则返回 fasle
- 左孩子不空,右孩子不空,但是两者 val 不同,则返回 false
此时就是就是左右不为空,并且val相等,
那么就应该比较外侧了,再比较内侧了。最后如果内侧外外侧都符合为true,就是对称二叉树。
class Solution {
public boolean isSymmetric(TreeNode root) {
if(root == null){
return true;
}
return compare(root.left,root.right);
}
public boolean compare(TreeNode node1, TreeNode node2){
// 两个都为空,对称
if(node1 == null && node2 == null){
return true;
}else if(node1 != null && node2 == null){ // 一个不空,一个空,不对称
return false;
}else if(node1 == null && node2 != null){ // 一个空,一个不空,不对称
return false;
}else if(node1.val != node2.val){ // 两个都不空,但是值不同,不对称
return false;
}
// 此时两个都不为空,值相同
// 比较外侧
boolean outside = compare(node1.left,node2.right);
// 比较内侧
boolean inside = compare(node1.right,node2.left);
return outside && inside;
}
}
代码很简单:但是我们要搞清楚,这个遍历的顺序是什么,从上面可以看出来是后序遍历。将左树,右树的结果返回给根节点。最后作判断!!
文章来源:https://blog.csdn.net/hero_jy/article/details/135255055
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!