数据结构和算法-最小生成树（prim和krusakal）和最短路径问题（BFS和dijkastra和floyd）

发布时间：2023年12月18日

最小生成树

总览

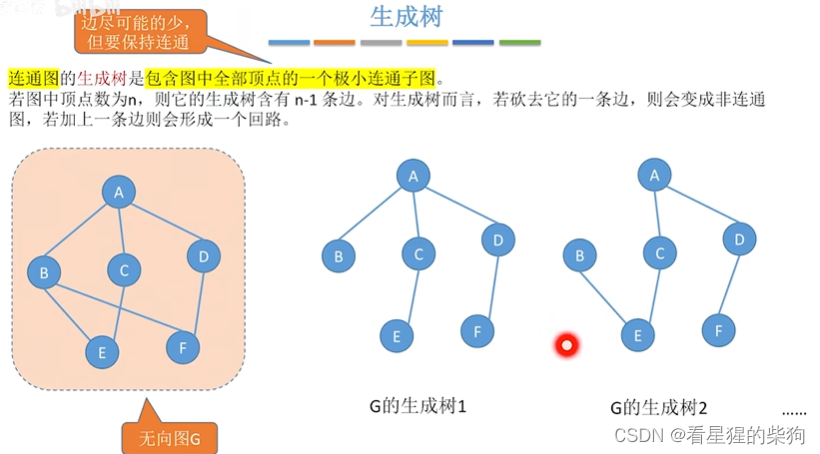
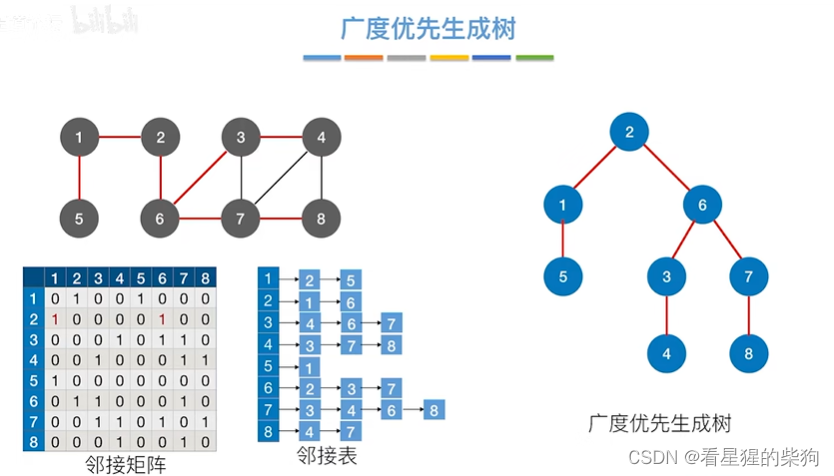
在这里插入图片描述

生成树

在这里插入图片描述

广度优先生成树

在这里插入图片描述

深度优先生成树

在这里插入图片描述

最小生成树

针对的是带权连通图
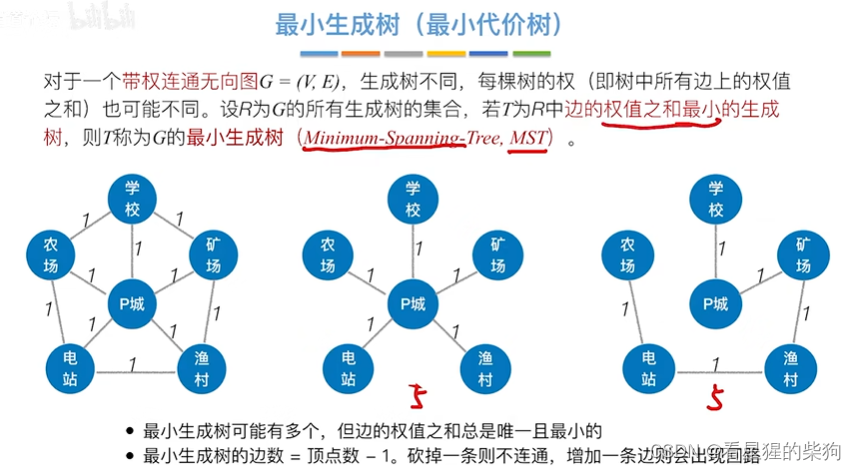
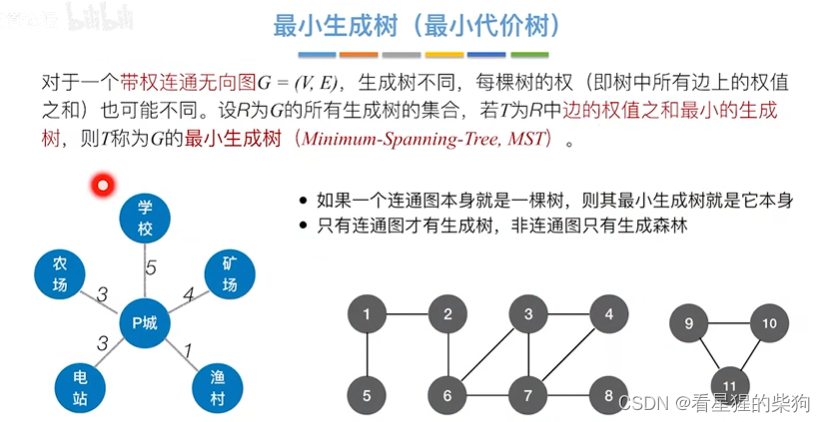
在这里插入图片描述

Prim算法

同一个图的最小生成树可能不唯一

从p城出发
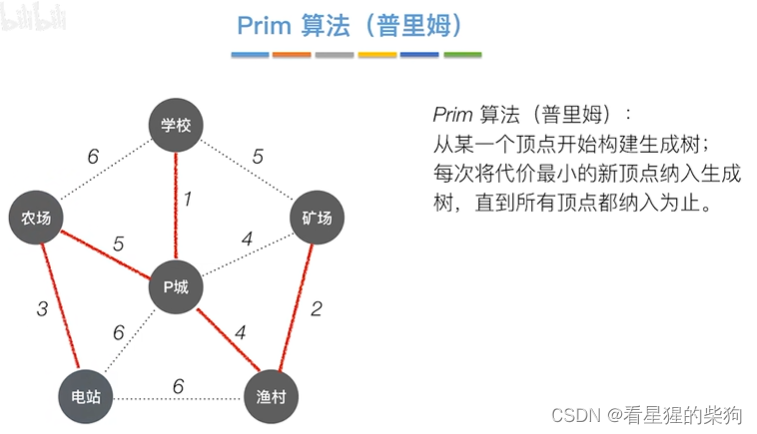
在这里插入图片描述

从农场出发也一样
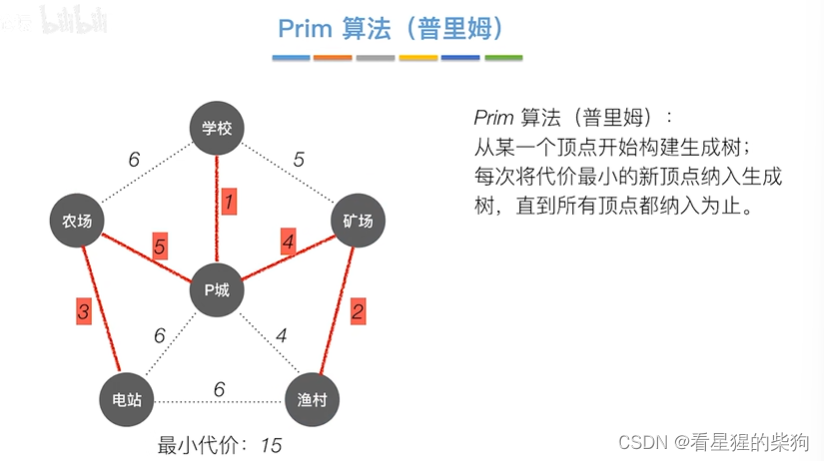
在这里插入图片描述

Kruskal算法

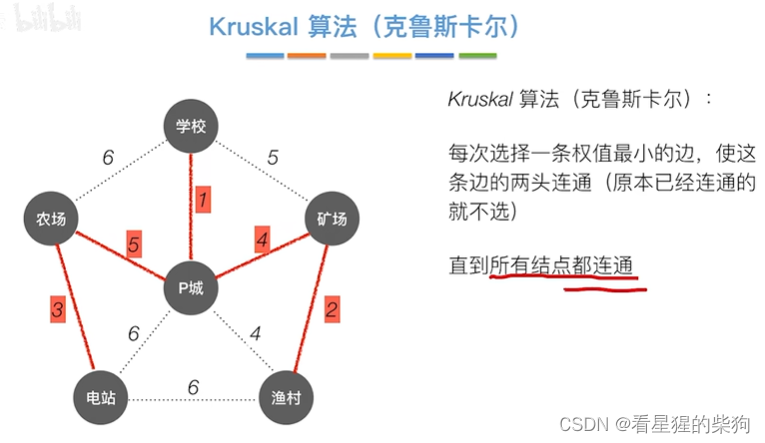
在这里插入图片描述

Prim vs Krusakal

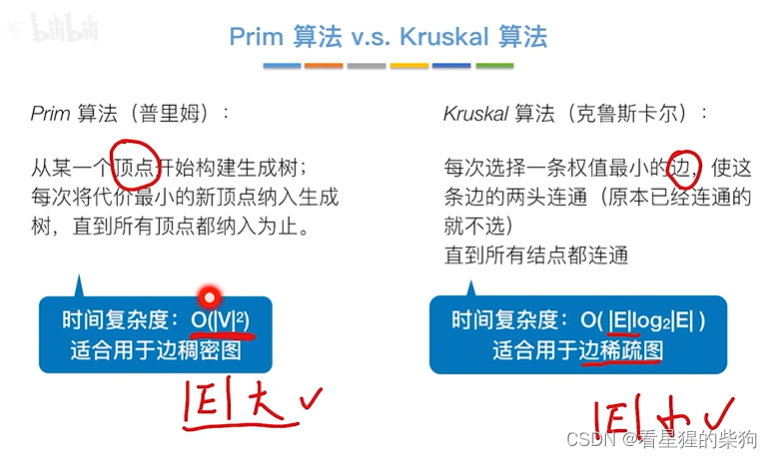
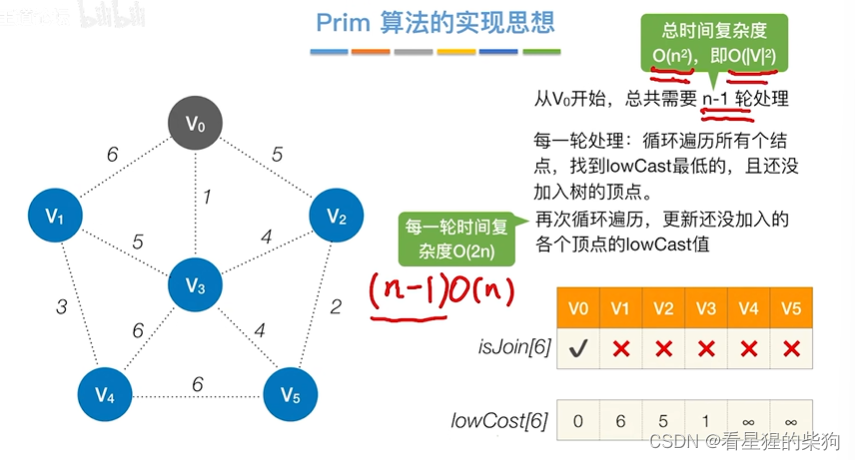
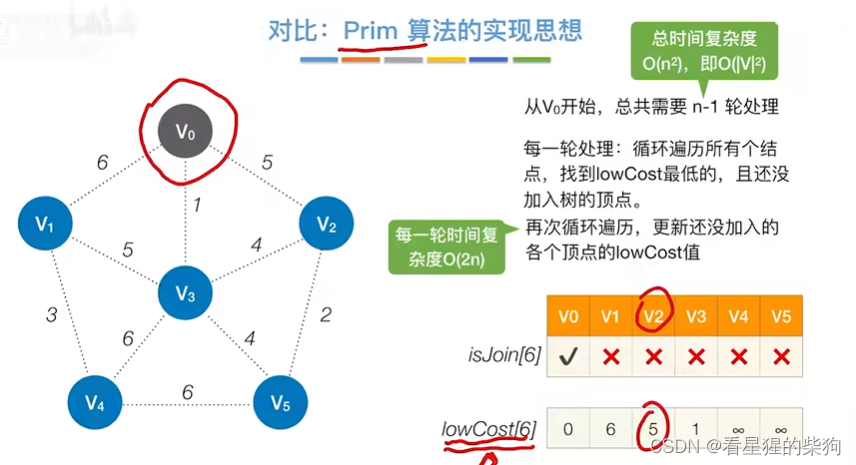
在这里插入图片描述

Prim的实现

先找到最低代价的节点，每次将节点加入树后，需要更新各节点加入树的最低代价（即将原来的代价和个节点与加入节点的代价作比较）
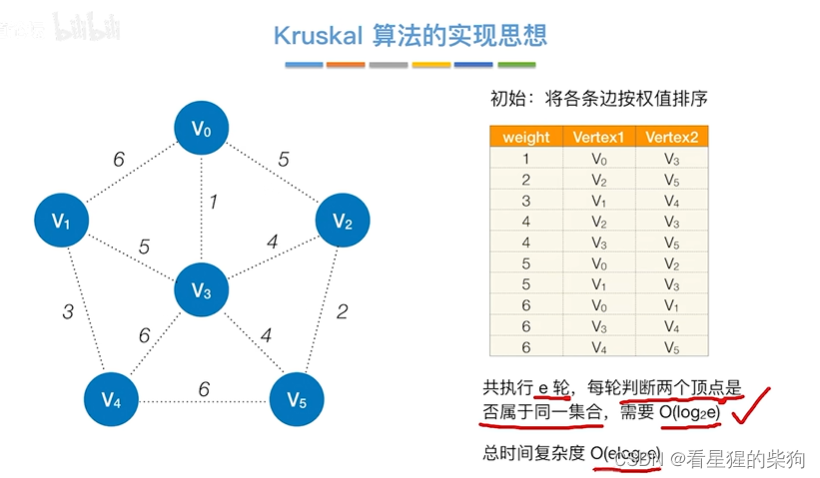
在这里插入图片描述

Kruskal的实现

查找并查集（如果用二叉树实现的）的根需要log2E
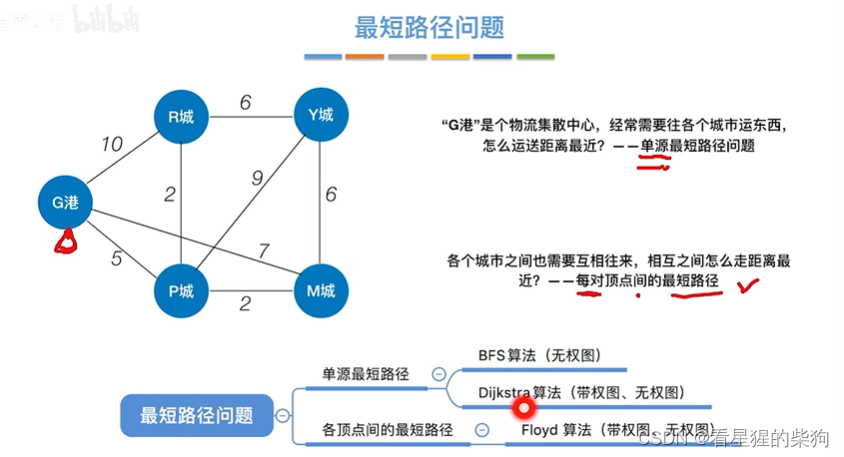
在这里插入图片描述

小结

在这里插入图片描述

最短路径问题

在这里插入图片描述

单源最短路径问题

BFS求无权图的单源最短路径

首先访问2号顶点，然后再更新其相邻顶点后的结果
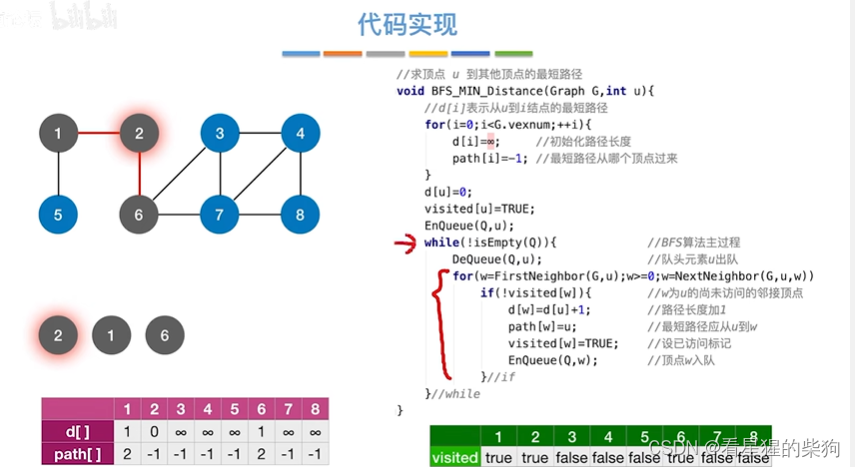
在这里插入图片描述
然后1号顶点出队，相邻节点入队，同时更新各相邻节点

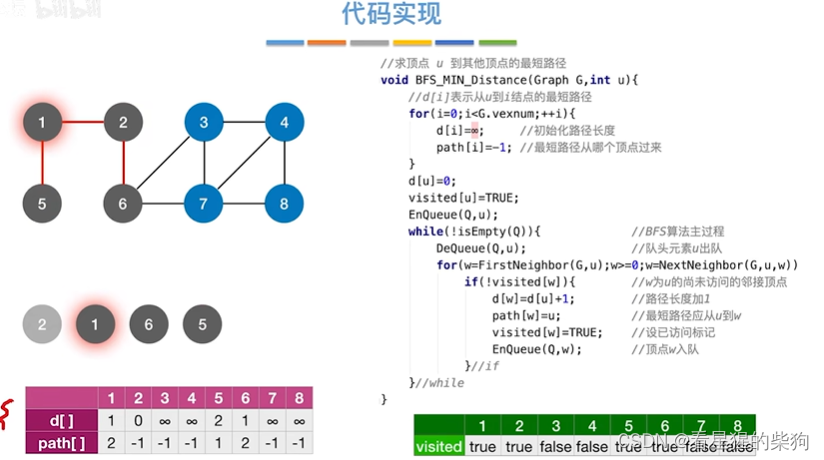
然后6号顶点出队，更新相邻节点，同时各个相邻节点入队

5号顶点没有相邻
所以到3号顶点处理

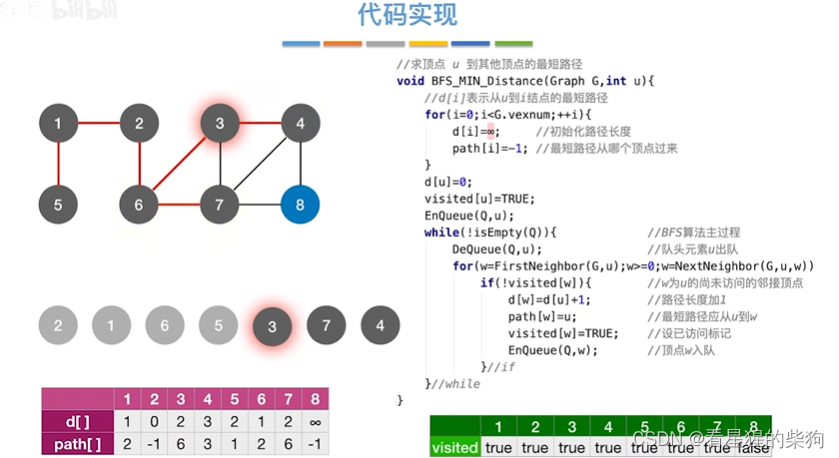
7号顶点处理

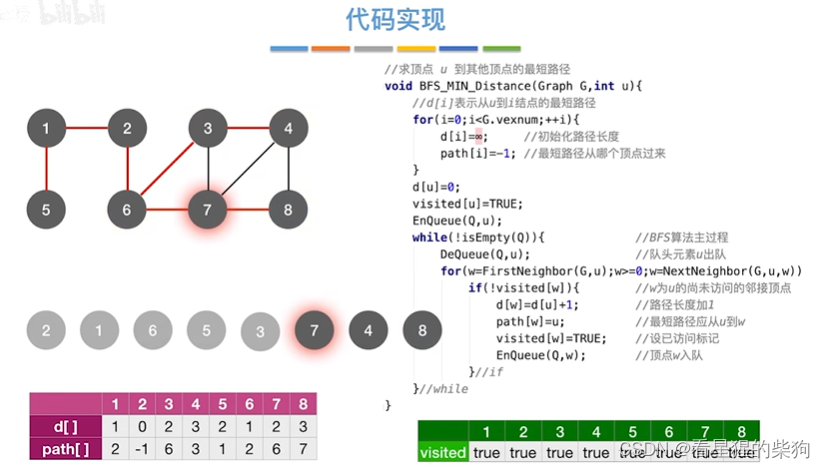
4号和8号相邻节点都被访问，所以没有处理

小结

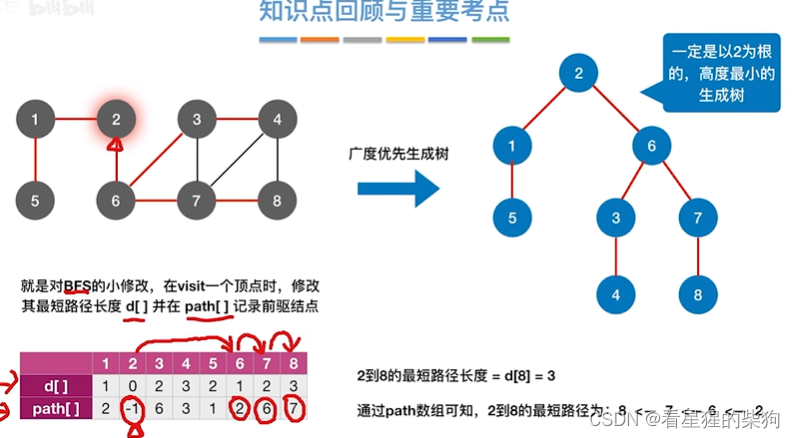
在这里插入图片描述

Dijkastra算法

BFS局限性（默认每条路径长度一样）
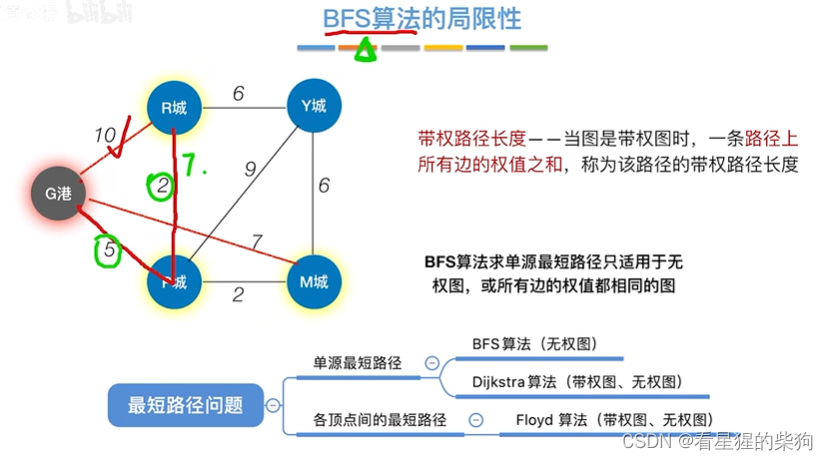
在这里插入图片描述
初始化后，即更新初始节点及其相邻节点

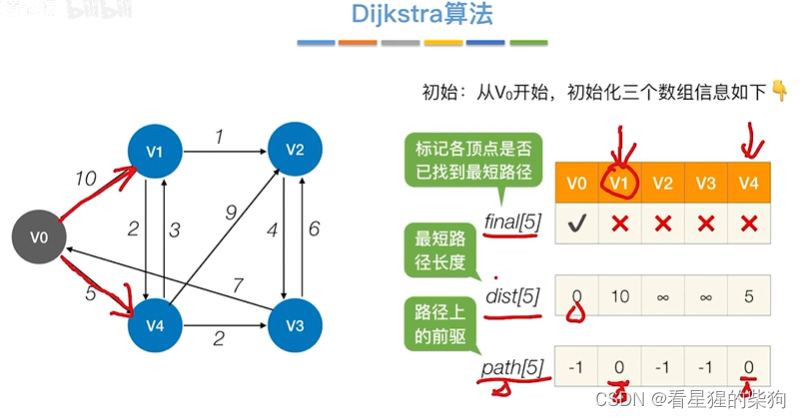
第一轮后

第二轮后

第三轮后
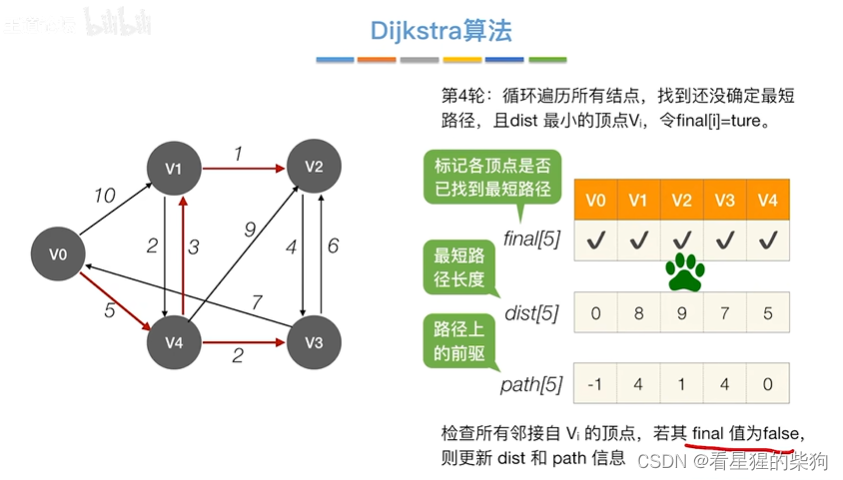
在这里插入图片描述
第四轮后

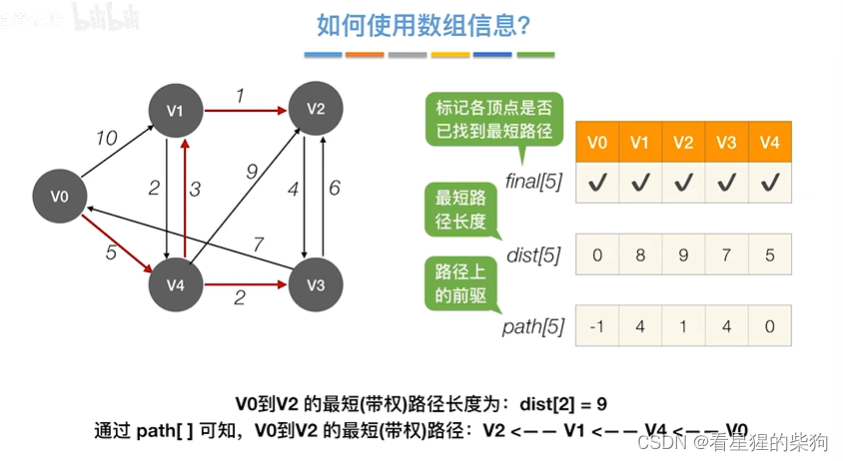
在这里插入图片描述
查找两个顶点的最短路径

算法时间复杂度

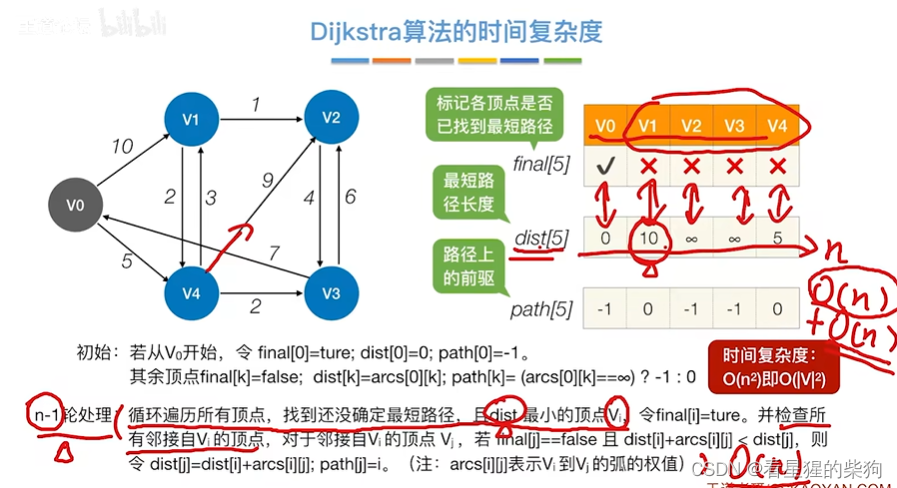
在这里插入图片描述

在这里插入图片描述

不适用情况

在这里插入图片描述

每一对顶点的最短路径问题

在这里插入图片描述

Floyd算法

初始时
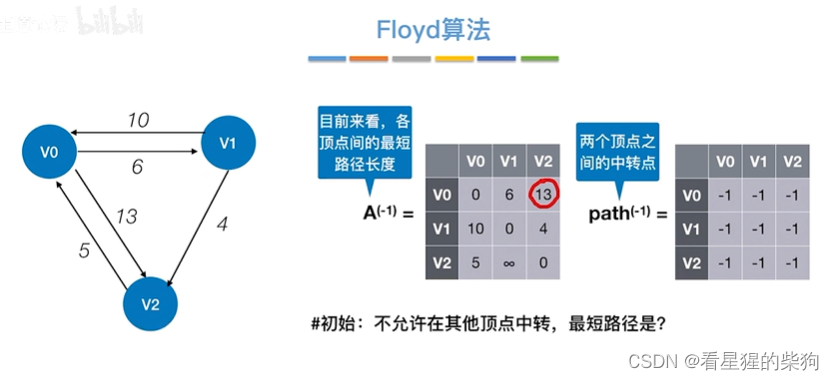
在这里插入图片描述
允许在v0中转

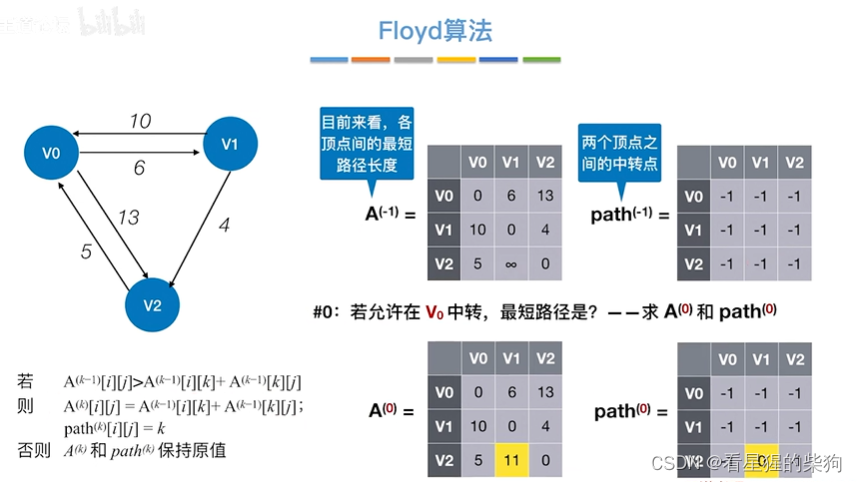
允许在v0 v1中转

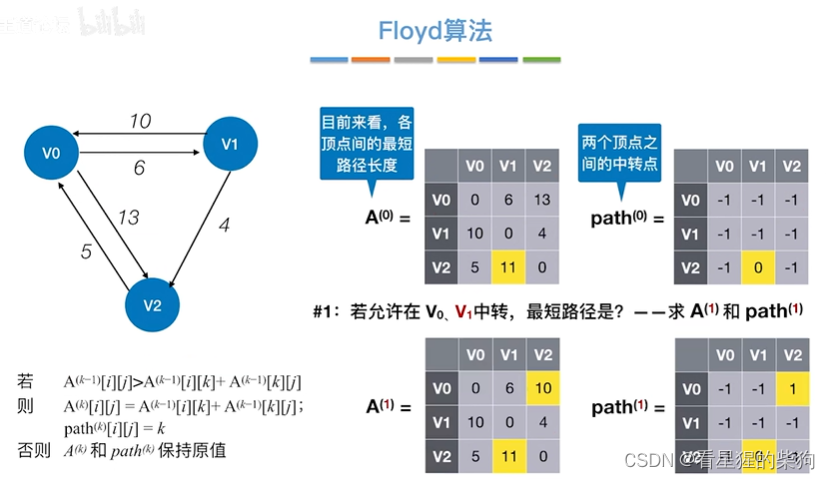
允许在v0 v1 v2中转

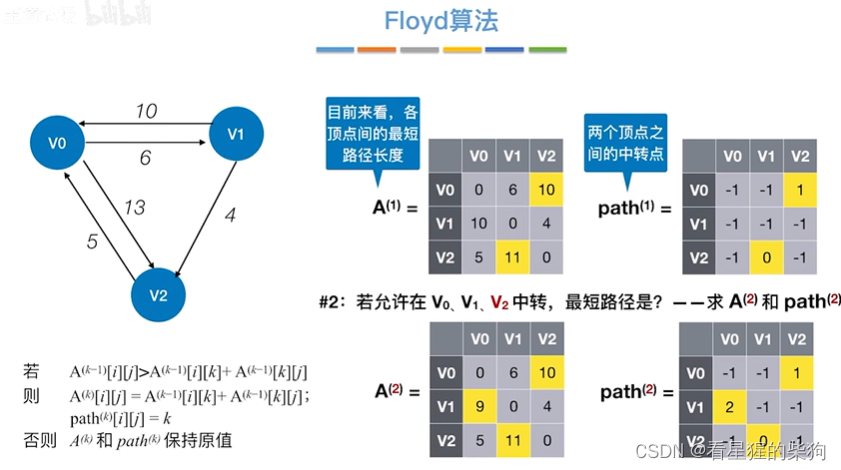
找两个点的最短路径

在这里插入图片描述

核心代码

空间复杂度是有n*n个矩阵那么多
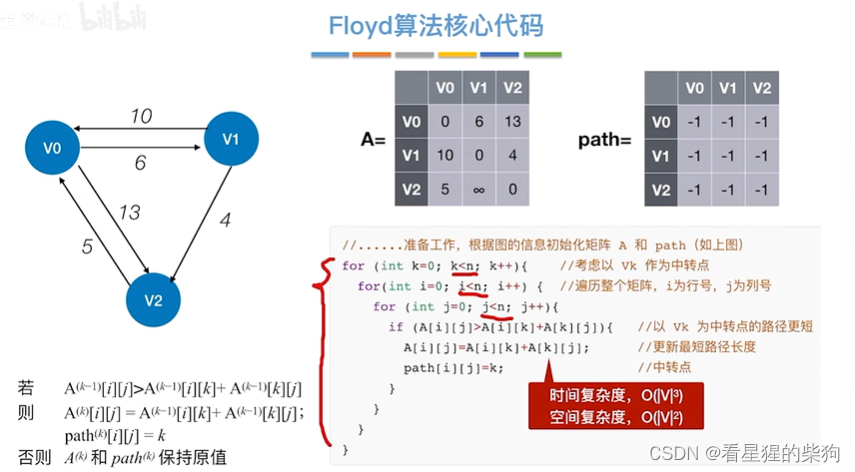
在这里插入图片描述

实例

初始
在这里插入图片描述
允许在v0中转
发现没有变化
从图可以发现v0没有进去的边，所以自然没法中转

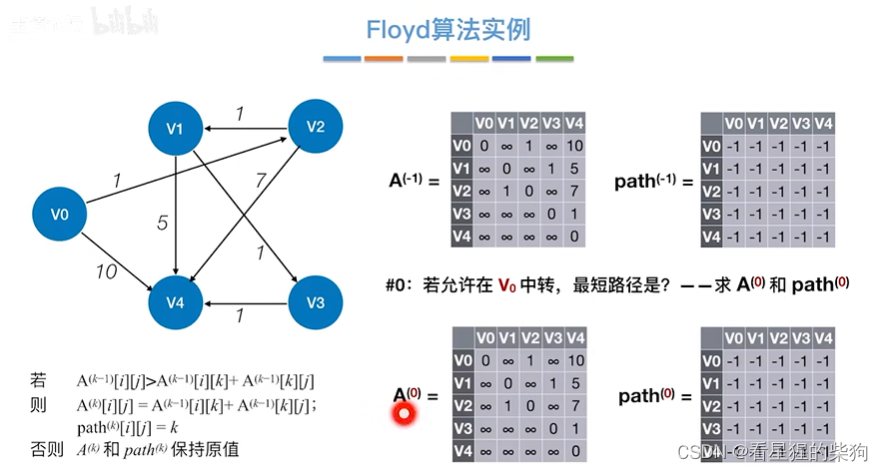
允许在v0 v1中转

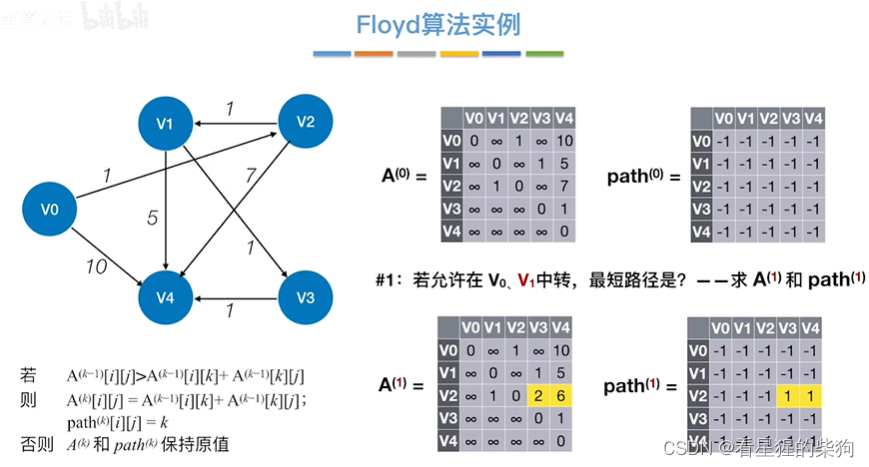
允许在v0 v1 v2中转
是已经基于之前v0 v1的中转结果的
例如v2到v3是基于中转v1的，但是在以v2中转的转换中是把它认为是相连的
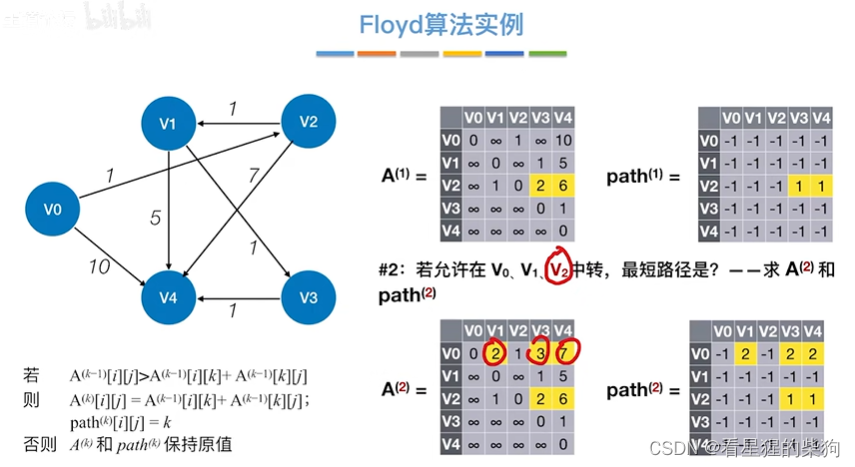
在这里插入图片描述

允许在v0 v1 v2 v3中转

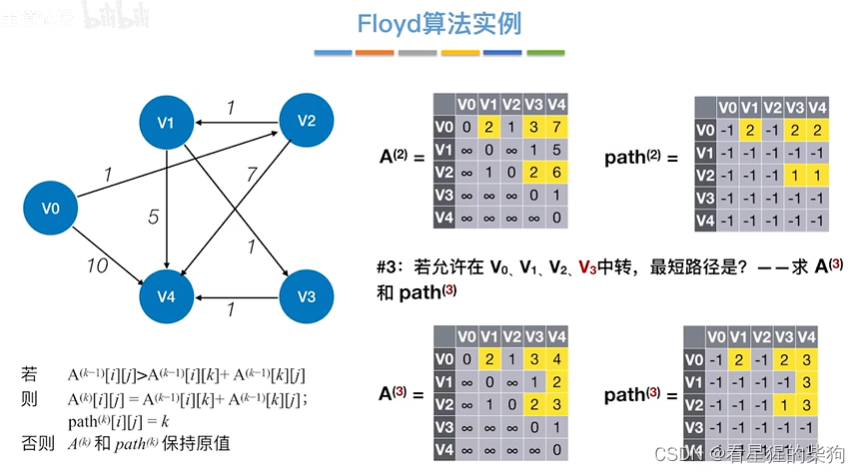
在这里插入图片描述
允许在v0 v1 v2 v3 v4中转

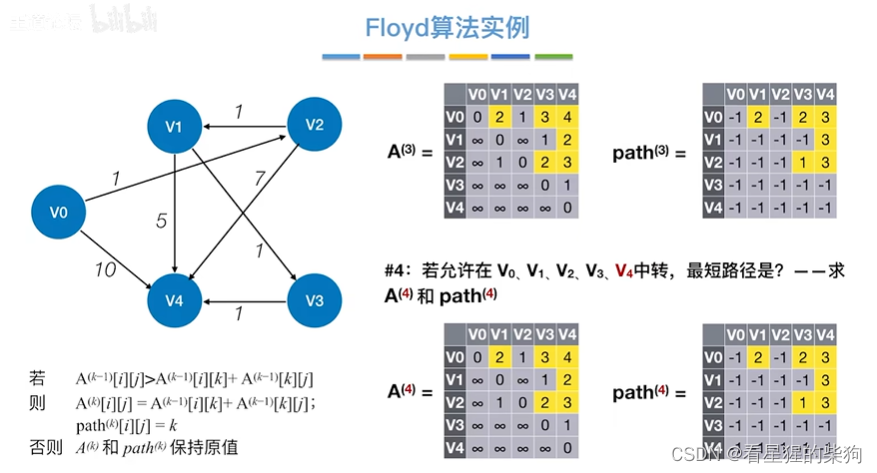
找两个顶点最短路径

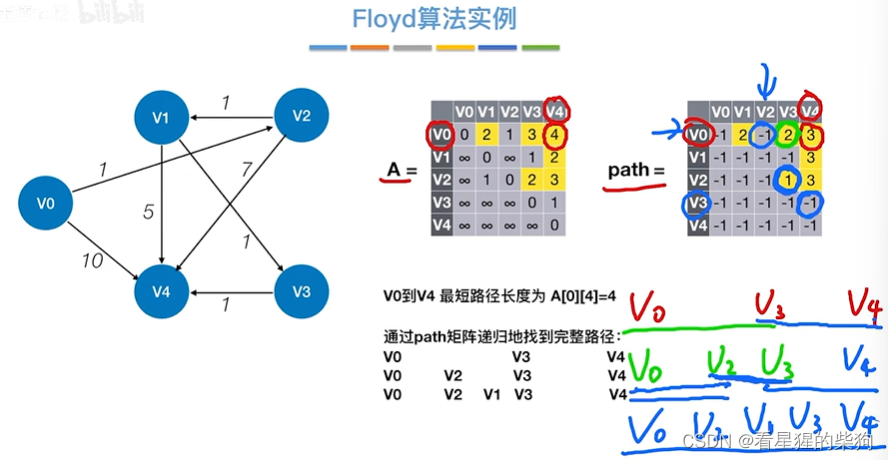
在这里插入图片描述

Floyd用于负权图

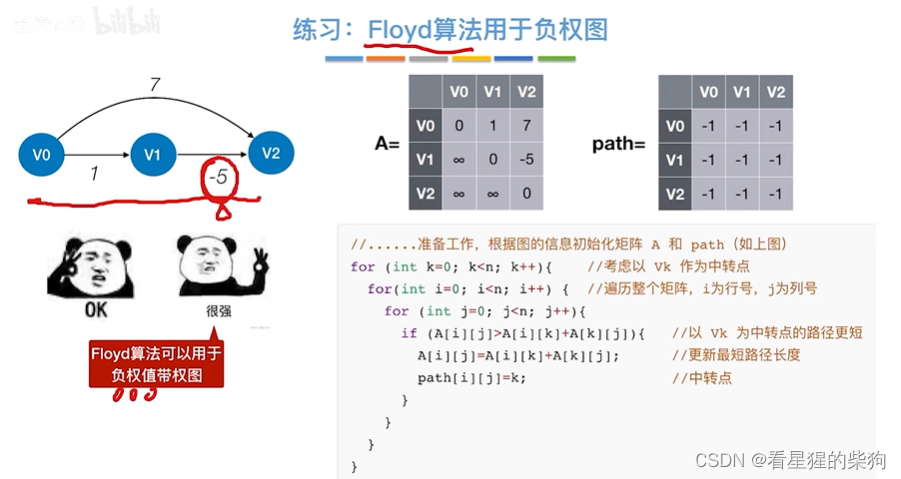
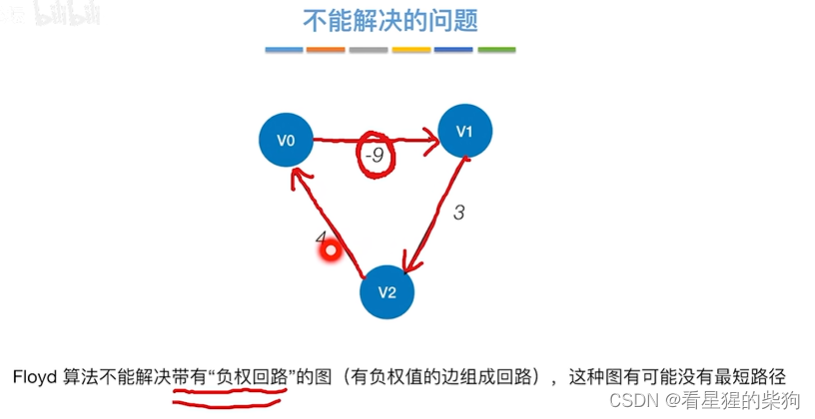
在这里插入图片描述

不能解决的问题

回路越多，路径越短

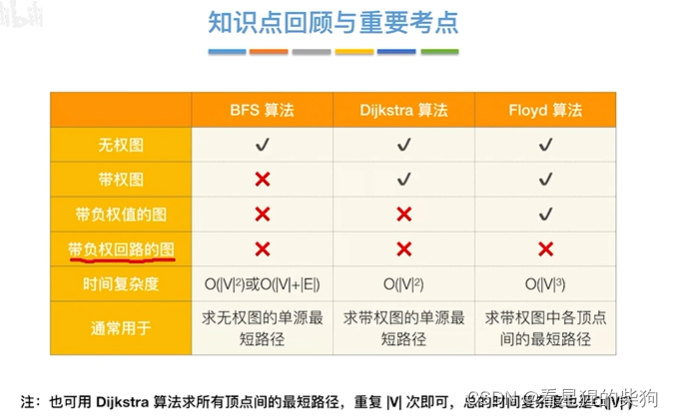
在这里插入图片描述

小结

BFS 采用邻接矩阵是V的平方邻接矩阵是V+E
在这里插入图片描述

文章来源:https://blog.csdn.net/llovewuzhengzi/article/details/135039877
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！

最新文章