代码随想录刷题题Day27

刷题的第二十七天，希望自己能够不断坚持下去，迎来蜕变。😀😀😀
刷题语言：C++
Day27 任务
● 62.不同路径
● 63. 不同路径 II

1 不同路径

62.不同路径

思路：
动态规划
机器人从(0 , 0) 位置出发，到(m - 1, n - 1)终点
（1）确定dp数组以及下标的含义

dp[i][j] ：表示从（0 ，0）出发，到(i, j) 有dp[i][j]条不同的路径

（2）确定递推公式
$dp[i][j]=dp[i?1][j]+dp[i][j?1]$

（3）dp数组如何初始化

dp[i][0]和dp[0][j]都是1

for (int i = 0; i < m; i++) dp[i][0] = 1;
for (int j = 0; j < n; j++) dp[0][j] = 1;

（4）遍历顺序

dp[i][j]都是从其上方和左方推导而来，那么从左到右一层一层遍历就可以

（5）举例推导dp数组

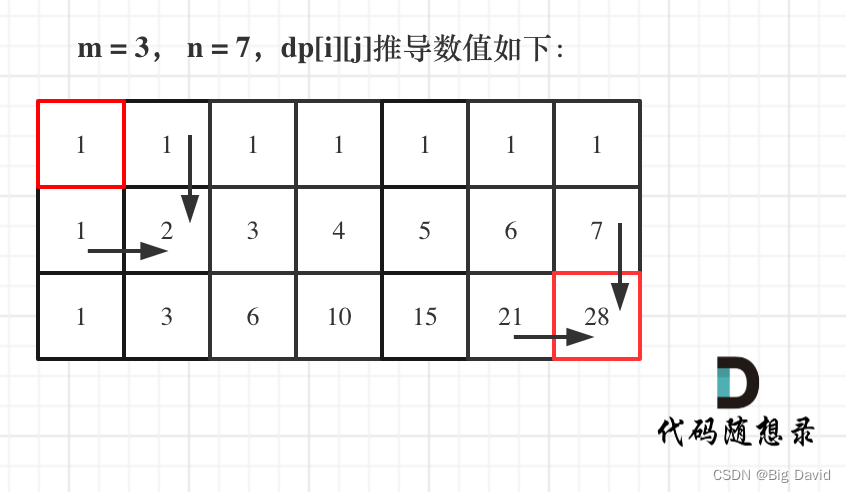
C++:

class Solution {
public:
    int uniquePaths(int m, int n) {
        vector<vector<int>> dp(m, vector<int>(n, 0));
        for (int i = 0; i < m; i++) dp[i][0] = 1;
        for (int j = 0; j < n; j++) dp[0][j] = 1;
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
            }
        }
        return dp[m - 1][n - 1];
    }
};

时间复杂度：$O(m\times n)$
空间复杂度：$O(m\times n)$

2 不同路径 II

63. 不同路径 II

思路：
动态规划
（1）确定dp数组以及下标的含义

dp[i][j] ：表示从（0 ，0）出发，到(i, j) 有dp[i][j]条不同的路径

（2）确定递推公式
$dp[i][j]=dp[i?1][j]+dp[i][j?1]$

有了障碍，(i, j)如果就是障碍的话应该就保持初始状态（初始状态为0）

if (obstacleGrid[i][j] == 0) { // 当(i, j)没有障碍的时候，再推导dp[i][j]
    dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}

（3）dp数组如何初始化

dp[i][0]和dp[0][j]都是1

vector<vector<int>> dp(m, vector<int>(n, 0));
for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) dp[i][0] = 1;
for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) dp[0][j] = 1;

（4）遍历顺序

dp[i][j]都是从其上方和左方推导而来，那么从左到右一层一层遍历就可以

for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                if (obstacleGrid[i][j] == 0) dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
            }
        }

（5）举例推导dp数组

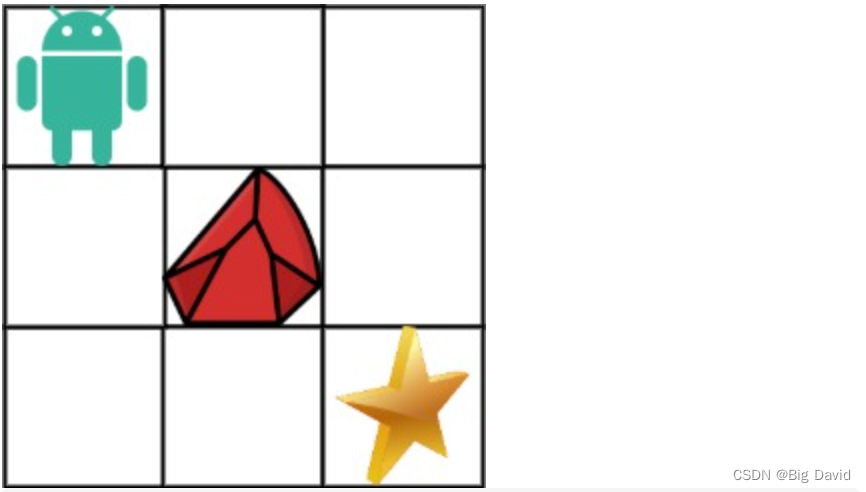
dp：

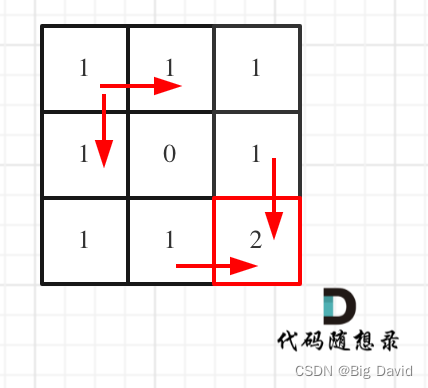
C++：

class Solution {
public:
    int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
        int m = obstacleGrid.size();
        int n = obstacleGrid[0].size();
        if (obstacleGrid[m - 1][n - 1] == 1 || obstacleGrid[0][0] == 1) return 0;
        vector<vector<int>> dp(m, vector<int>(n, 0));
        for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) dp[i][0] = 1;
        for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) dp[0][j] = 1;
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                if (obstacleGrid[i][j] == 0) dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
            }
        }
        return dp[m - 1][n - 1];
    }
};

时间复杂度：$O(n\times m)$，n、m 分别为obstacleGrid 长度和宽度
空间复杂度：$O(n\times m)$

---

鼓励坚持二十八天的自己😀😀😀