ARIMA 模型

发布时间：2024年01月22日

目的

????????预测

要求

????????数据具有平稳性——“惯性”，平稳性要求数据的均值和方差不发生明显变化。

? ? ? ? 严平稳：分布不随时间的改变而改变。
? ? ? ? 弱平稳（大部分）：期望与相关系数（依赖性）不变。未来某时刻的值X要依赖于它过去信息，所以需要依赖性。

差分法

? ? ? ? 用以让不够平稳的数据变平稳

? ? ? ? 方法如其名

? ? ? ? 差分的实现

import sys
import os
import pandas as pd
import numpy as np

import statsmodels.api as sm
import statsmodels.formula.api as smf
import statsmodels.tsa.api as smt
import matplotlib.pylab as plt

import seaborn as sns

pd.set_option('display.float_format', lambda x: '%.5f' % x)
np.set_printoptions(precision=5, suppress=True)
pd.set_option('display.max_columns', 100)
pd.set_option('display.max_rows', 100)
sns.set(style='ticks', context='poster')

Sentiment = 'data.csv'
Sentiment = pd.read_csv(Sentiment, index_col=0, parse_dates=[0])
print(Sentiment)
Sentiment.plot(figsize=(12,8))
plt.legend(bbox_to_anchor=(1.25, 0.5))
plt.title("Consumer Sentiment")
sns.despine()


Sentiment['col3'] = Sentiment['col2'].diff(1)  # 求差分值，一阶差分。1指的是1个时间间隔，可更改。

Sentiment['col4'] = Sentiment['col3'].diff(1)  # 再求差分，二阶差分。
print(Sentiment)
Sentiment.plot(subplots=True, figsize=(18, 12))

plt.show()

自回归模型（AR）

????????描述当前值与历史值之间的关系，用变量自身的历史时间数据对自身进行预测

? ? ? ? 必须满足平稳性

? ? ? ? 阶数指时间间隔

? ? ? ? p阶自回归过程的公式

???????????????? $y_t = \mu + \sum_{i=1}^{p} \gamma_i y_{t - i} + \epsilon_t$

? ? ? ? $\mu$ 是常数项， $\gamma_i$ 是自相关系数， $\epsilon_t$ 是误差。

? ? ? ? p自己选定?

? ? ? ? 限制

? ? ? ? 必须具有自相关性，若自相关系数小于0.5则不宜采用。

移动平均模型（MA）

? ? ? ? 关注自回归模型中的误差项的累加

? ? ? ? q阶自回归过程的公式

???????? $y_t = \mu + \epsilon_t + \sum_{i=1}^{q} \theta_i \epsilon_{t - i}$

? ? ? ? 能有效消除随机波动

差分自回归移动模型（ARIMA）?

? ? ? ? AR 与 MA结合，I指差分

???????? $y_t = \mu + \sum_{i=1}^{p} \gamma_i y_{t - i} + \epsilon_t + \sum_{i=1}^{q} \theta_i \epsilon_{t - i}$

? ? ? ? 指定参数（p，d，q），d是差分的次数，一般1次就够

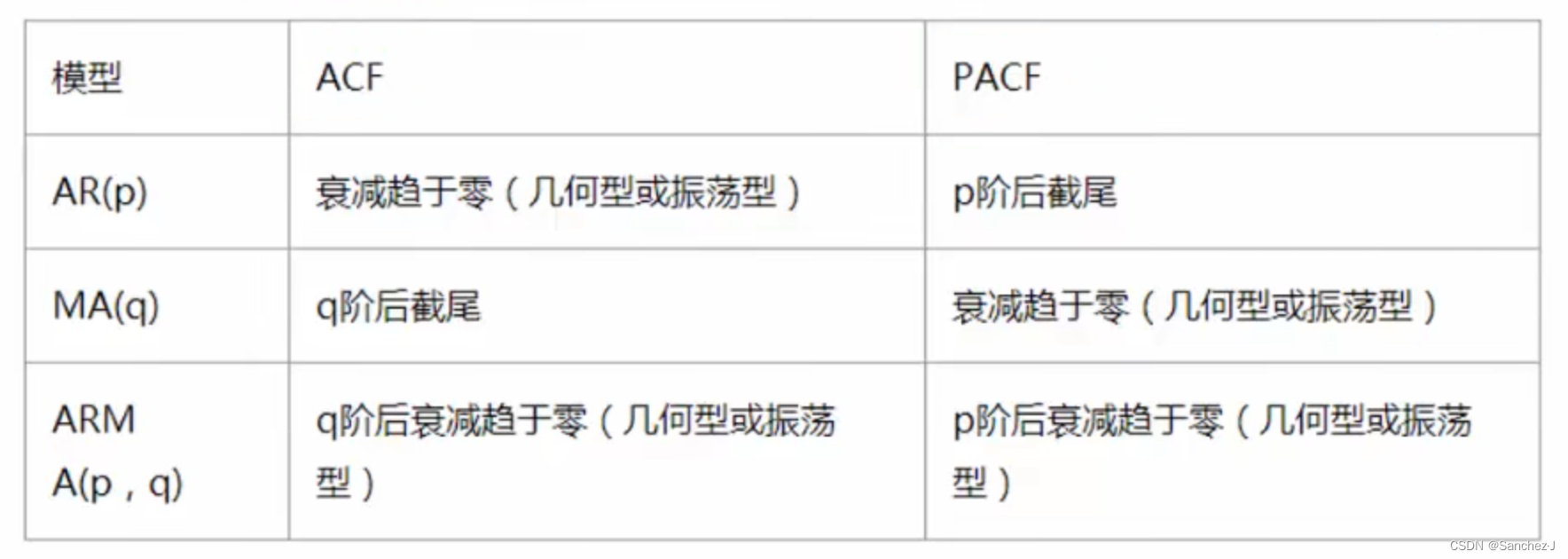
?参数pq的选取

? ? ? ? 自相关函数ACF（autocorrelation function）

? ? ? ? ? ? ? ? 有序的随机变量序列与其自身相比较

? ? ? ? ? ? ? ? 反映同一序列在不同时序的取值之间的相关性

? ? ? ? ? ? ? ? 公式

???????????????????????? $ACF(k) = \rho_k = \frac{Cov(y_t,y_{t-k})}{Var(y_t)}$

? ? ? ? ? ? ? ? 取值范围[-1, 1]?

? ? ? ? 偏自相关函数（PACF）

? ? ? ? ? ? ? ? ACF还受其他阶数变量影响，PACF剔除中间的影响，只保留yt和yt-k的关系。

import statsmodels.api as sm
import pandas as pd
import matplotlib.pylab as plt

# read data
rd_data = pd.read_csv('data.csv')
data = pd.Series([x for x in rd_data['col2']], index=[y for y in rd_data['col1']])
print(data)

fig = plt.figure(figsize=(12, 8))
# acf
ax1 = fig.add_subplot(211)
fig = sm.graphics.tsa.plot_acf(data, lags=20, ax=ax1)
ax1.xaxis.set_ticks_position('bottom')
fig.tight_layout()
# pacf
ax2 = fig.add_subplot(212)
fig = sm.graphics.tsa.plot_pacf(data, lags=20, ax=ax2)
ax2.xaxis.set_ticks_position('bottom')

plt.show()

阶数确定

? ? ? ? 截尾：落入置信区间内?

? ? ? ? 奇异点、离群点不管

? ? ? ? 散点图?

????????

# 散点图
import pandas as pd
import numpy as np
import matplotlib.pylab as plt
import seaborn as sns
# read data
rd_data = pd.read_csv('data.csv')
data = pd.Series([x for x in rd_data['col2']], index=[y for y in rd_data['col1']])

lags = 9
ncols = 3
nrows = int(np.ceil(lags / ncols))

fig, axes = plt.subplots(ncols=ncols, nrows=nrows, figsize=(4 * ncols, 4 * nrows))

for ax, lag in zip(axes.flat, np.arange(1, lags + 1, 1)):
    lag_str = 't-{}'.format(lag)
    X = (pd.concat([data, data.shift(-lag)], axis=1, keys=['y'] + [lag_str]).dropna())

    X.plot(ax=ax, kind='scatter', y='y', x=lag_str)
    corr = X.corr().values[0][1]
    ax.set_ylabel('Original')
    ax.set_title('Lag: {} (corr={:.2f})'.format(lag_str, corr))
    ax.set_aspect('equal')
    sns.despine()

fig.tight_layout()
plt.show()

ARIMA建模流程

将序列平稳（差分法确定d）
p阶和q阶数确定：ACF与PACF
ARIMA（p,d,q）?

模板

# 模板
import pandas as pd
import numpy as np
import matplotlib.pylab as plt
import seaborn as sns
import statsmodels.api as sm
def tsplot(y, lags=None, title='', figsize=(14, 8)):
    fig = plt.figure(figsize=figsize)
    layout = (2, 2)
    ts_ax = plt.subplot2grid(layout, (0, 0))
    hist_ax = plt.subplot2grid(layout, (0, 1))
    acf_ax = plt.subplot2grid(layout, (1, 0))
    pacf_ax = plt.subplot2grid(layout, (1, 1))

    y.plot(ax=ts_ax)
    ts_ax.set_title(title)
    y.plot(ax=hist_ax, kind='hist', bins=25)
    hist_ax.set_title('Histogram')
    sm.graphics.tsa.plot_acf(y, lags=lags, ax=acf_ax)
    sm.graphics.tsa.plot_pacf(y, lags=lags, ax=pacf_ax)
    [ax.set_xlim(0) for ax in [acf_ax, pacf_ax]]
    sns.despine()
    plt.tight_layout()
    return ts_ax, acf_ax, pacf_ax


# read data
rd_data = pd.read_csv('data.csv')
data = pd.Series([x for x in rd_data['col2']], index=[y for y in rd_data['col1']])


tsplot(data, title='Random data', lags=36)
plt.show()

评估

? ? ? ? 模型选择AIC与BIC：选择更简单的模型

? ? ? ?? $AIC = 2k - sln(L)$

? ? ? ?? $BLC = kln(n) - 2ln(L)$

? ? ? ? k为模型参数个数，n为样本数量，L为似然函数

? ? ? ? 选小的

????????

import sys
import os
import pandas as pd
import numpy as np

import statsmodels.api as sm
import statsmodels.formula.api as smf
import statsmodels.tsa.api as smt

# Display and Plotting
import matplotlib.pylab as plt
import seaborn as sns

pd.set_option('display.float_format', lambda x: '%.5f' % x)  # pandas
np.set_printoptions(precision=5, suppress=True)  # numpy

pd.set_option('display.max_columns', 100)
pd.set_option('display.max_rows', 100)

# seaborn plotting style
sns.set(style='ticks', context='poster')

filename_ts = 'data.csv'
ts_df = pd.read_csv(filename_ts, index_col=1, parse_dates=[0])

n_sample = ts_df.shape[0]

print(ts_df.shape)
print(ts_df.head())
# Create a training sample and testing sample before analyzing the series
n_train = int(0.95 * n_sample) + 1
# 计算训练样本的大小。这里使用 95% 的数据作为训练集，+1 用于确保至少有一个样本在测试集中。
n_forecast = n_sample - n_train
# 计算预测样本的大小。
ts_train = ts_df.iloc[:n_train]['col1']
# 从时间序列数据框中选择前 n_train 行作为训练样本.
ts_test = ts_df.iloc[n_train:]['col1']
# 从时间序列数据框中选择从第 n_train 行开始到最后一行的数据作为测试样本，
print(ts_train.shape)
print(ts_test.shape)
print("Training Series:", "\n", ts_train.tail(), "\n")
print("Testing Series:", "\n", ts_test.head())


def tsplot(y, lags=None, title='', figsize=(14, 8)):
    fig = plt.figure(figsize=figsize)
    layout = (2, 2)
    ts_ax = plt.subplot2grid(layout, (0, 0))
    hist_ax = plt.subplot2grid(layout, (0, 1))
    acf_ax = plt.subplot2grid(layout, (1, 0))
    pacf_ax = plt.subplot2grid(layout, (1, 1))

    y.plot(ax=ts_ax)
    ts_ax.set_title(title)
    y.plot(ax=hist_ax, kind='hist', bins=25)
    hist_ax.set_title('Histogram')
    sm.graphics.tsa.plot_acf(y, lags=lags, ax=acf_ax)
    sm.graphics.tsa.plot_pacf(y, lags=lags, ax=pacf_ax)
    [ax.set_xlim(0) for ax in [acf_ax, pacf_ax]]
    sns.despine()
    plt.tight_layout()
    return ts_ax, acf_ax, pacf_ax


tsplot(ts_train, title='A Given Training Series', lags=20)
plt.show()

'''
arima200 = sm.tsa.SARIMAX(ts_train, order=(2, 0, 0))# order里边的三个参数p,d,q
model_results = arima200.fit()# fit模型
'''

train_results = sm.tsa.arma_order_select_ic(ts_train, ic=['aic', 'bic'], trend='n', max_ar=4, max_ma=4)

print('AIC', train_results.aic_min_order)
print('BIC', train_results.bic_min_order)

模型残差检查?

????????残差是否是平均值为0且方差是常数的正态分布

? ? ? ? QQ图：线性即正态分布

import sys
import os
import pandas as pd
import numpy as np

import statsmodels.api as sm
import statsmodels.formula.api as smf
import statsmodels.tsa.api as smt

# Display and Plotting
import matplotlib.pylab as plt
import seaborn as sns

pd.set_option('display.float_format', lambda x: '%.5f' % x)  # pandas
np.set_printoptions(precision=5, suppress=True)  # numpy

pd.set_option('display.max_columns', 100)
pd.set_option('display.max_rows', 100)

# seaborn plotting style
sns.set(style='ticks', context='poster')

filename_ts = 'data.csv'
ts_df = pd.read_csv(filename_ts, index_col=1, parse_dates=[0])

n_sample = ts_df.shape[0]

print(ts_df.shape)
print(ts_df.head())
# Create a training sample and testing sample before analyzing the series
n_train = int(0.95 * n_sample) + 1
# 计算训练样本的大小。这里使用 95% 的数据作为训练集，+1 用于确保至少有一个样本在测试集中。
n_forecast = n_sample - n_train
# 计算预测样本的大小。
ts_train = ts_df.iloc[:n_train]['col1']
# 从时间序列数据框中选择前 n_train 行作为训练样本.
ts_test = ts_df.iloc[n_train:]['col1']
# 从时间序列数据框中选择从第 n_train 行开始到最后一行的数据作为测试样本，
print(ts_train.shape)
print(ts_test.shape)
print("Training Series:", "\n", ts_train.tail(), "\n")
print("Testing Series:", "\n", ts_test.head())


def tsplot(y, lags=None, title='', figsize=(14, 8)):
    fig = plt.figure(figsize=figsize)
    layout = (2, 2)
    ts_ax = plt.subplot2grid(layout, (0, 0))
    hist_ax = plt.subplot2grid(layout, (0, 1))
    acf_ax = plt.subplot2grid(layout, (1, 0))
    pacf_ax = plt.subplot2grid(layout, (1, 1))

    y.plot(ax=ts_ax)
    ts_ax.set_title(title)
    y.plot(ax=hist_ax, kind='hist', bins=25)
    hist_ax.set_title('Histogram')
    sm.graphics.tsa.plot_acf(y, lags=lags, ax=acf_ax)
    sm.graphics.tsa.plot_pacf(y, lags=lags, ax=pacf_ax)
    [ax.set_xlim(0) for ax in [acf_ax, pacf_ax]]
    sns.despine()
    plt.tight_layout()
    return ts_ax, acf_ax, pacf_ax


tsplot(ts_train, title='A Given Training Series', lags=20)
plt.show()



train_results = sm.tsa.arma_order_select_ic(ts_train, ic=['aic', 'bic'], trend='n', max_ar=4, max_ma=4)

print('AIC', train_results.aic_min_order)
print('BIC', train_results.bic_min_order)

arima200 = sm.tsa.SARIMAX(ts_train, order=(2, 0, 0))# order里边的三个参数p,d,q
model_results = arima200.fit()# fit模型
model_results.plot_diagnostics(figsize=(16, 12))# statsmodels库
plt.show()

文章来源:https://blog.csdn.net/qq_43010742/article/details/135712153
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！