【本科生通信原理】【实验报告】【北京航空航天大学】实验一：通信原理初步

一、实验目的：

1. 熟悉 MATLAB开发环境、掌握 MATLAB基本运算操作；
2. 熟悉和了解 MATLAB图形绘制基本指令；
3. 熟悉使用 MATLAB分析信号频谱的过程；
4. 掌握加性白高斯噪声信道模型

二、实验内容：

三、实验程序：
1、

function q1()
x = 0 : 0.0001 : 2 * pi;
y1 = 2 * exp(-0.5 * x);
y2 = cos(4 * pi * x);
figure;
plot(x, y1);
hold;
plot(x, y2);
xlabel("x", "FontName", "Times New Roman", "FontSize", 12);
ylabel("y", "FontName", "Times New Roman", "FontSize", 12);
legend("FontName","Times New Roman", "FontSize", 10, "LineWidth", 1.5);
legend("y1", "y2");
title("q1");
axis([0 2 * pi -1.1 2.1]);
grid;

2、

function q2()
x = 0 : 0.01 : 10;  % 横坐标区间
R = normrnd(0, sqrt(0.1), 1, length(x));  % 生成1 * length(x)个正态随机数
 
figure;  % 画信号波形
plot(x, R);
grid on;
title('White Gaussian Noise');
xlabel('x');
ylabel('N');
 
figure;  % 画序列柱状图
bar(R);
grid on;
title('Bar Graph of Noise Sequence');
xlabel('n');
ylabel('N');

3、

function q3()
N = 1024;  %采样点数
ts = 0.6 / 1023;  %系统时域采样间隔
fs = 1 / ts;  %系统采样频率
df = 0.001;  %所需的频率分辨率
t = 0 : ts: 0.6;
x = 0.4 * sin(100 * pi * t) + 0.4 * sin(640 * pi * t);
n = randn(1, N);  % 噪声信号（噪声方差为1）
y = x + n;  % 原始信号叠加噪声信号
[Y, m, df1, f] = T2F(y, ts, df, fs);

figure;  % 画信号时域波形图
plot(t, y);
grid on;
title('信号时域波形图');
xlabel('t/s');
ylabel('y(t)');
 
figure;  % 画信号频谱图
plot(f, abs(Y));
grid on;
title('信号频谱图');
xlabel('w');
ylabel('Y(w)');

4、

function q4()
% AM调制解调
echo on;
N = 1024;  % 采样点数
A = 3;  % 直流分量
fc = 125;  %载波频率
t0 = 0.6;  %信号持续时间
snr = 10;  %解调器输入信噪比dB
dt = 0.6 / 1023;  %系统时域采样间隔
fs = 1 / dt;  %系统采样频率
df = 0.001;  %所需的频率分辨率
t = 0 : dt : t0;
m = 0.1 * cos(15 * pi * t) + 1.5 * sin(25 * pi * t) + 0.5 * cos(40 * pi * t);  %调制信号
c = cos(250 * pi * t);  %载波
Lt = length(t);  %仿真过程中，信号长度
snr_lin = 10 ^ (snr / 10);  %信噪比
L = 2 * min(m);
R = 2 * max(abs(m)) + A;
[M, m, df1, f] = T2F(m, dt, df, fs);  %求出调制信号频谱
[Bw_eq] = signalband(M, df, t0);  %求出信号等效带宽
u = (A + m(1 : Lt)) .* c(1 : Lt);  % 已调信号
[U, u, df1, f] = T2F(u, dt, df, fs);
signal_power = power_x(u(1 : Lt));  %已调信号的平均功率
noise_power = (signal_power * fs) / (snr_lin * (2 * Bw_eq));  %求出噪声方差（噪声均值为0）
noise_std = sqrt(noise_power);  %噪声标准差
noise = noise_std * randn(1, Lt);  %产生噪声
sam = u(1 : Lt) + noise(1 : Lt);  %叠加了噪声的已调信号
[SAM, sam, df1, f] = T2F(sam, dt, df, fs);  %求出叠加了噪声的已调信号频谱
 
figure;  % 画出经过信道前的已调信号时域波形
plot(t, u(1 : length(t)));
grid on;
title('经过AWGN信道前的已调信号的时域波形图');
xlabel('t');
ylabel('u(t)');
 
figure;  %画出经过信道前的已调信号频谱图
plot(f, abs(fftshift(U)));
grid on;
title('经过AWGN信道前的已调信号的频谱图');
xlabel('w');
ylabel('U(w)');
 
figure;  %画出经过信道后的已调信号时域波形
plot(t, sam(1 : length(t)));
axis([0 t0 -20 20]);
grid on;
title('经过AWGN信道后的已调信号的时域波形图');
xlabel('t');
ylabel('s(t)');
 
figure;  %画出经过信道后的已调信号频谱图
plot(f, abs(fftshift(SAM)));
grid on;
title('经过AWGN信道后的已调信号的时域波形图');
xlabel('w');
ylabel('S(w)');

四、实验结果：
1、

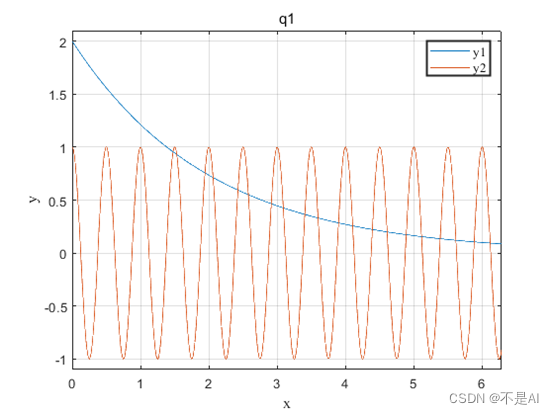
2、
（1）、信号波形：

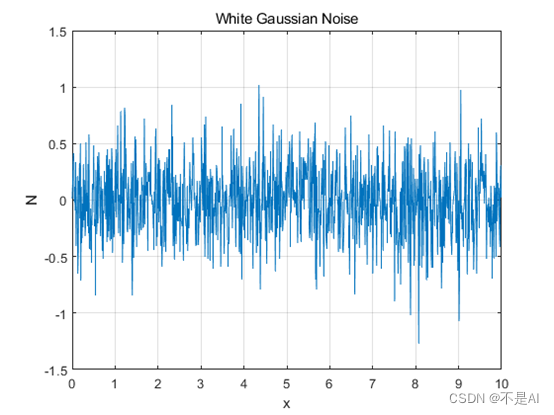
（2）、序列柱状图：

3、
（1）、所得信号的时域波形图：

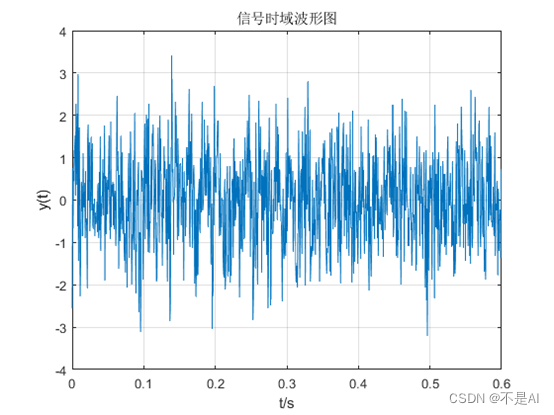
（2）、所得信号的频谱图：

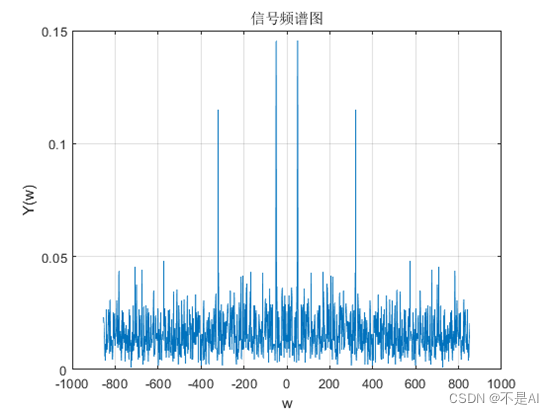
4、
（1）、经过AWGN信道前的已调信号的时域波形图：

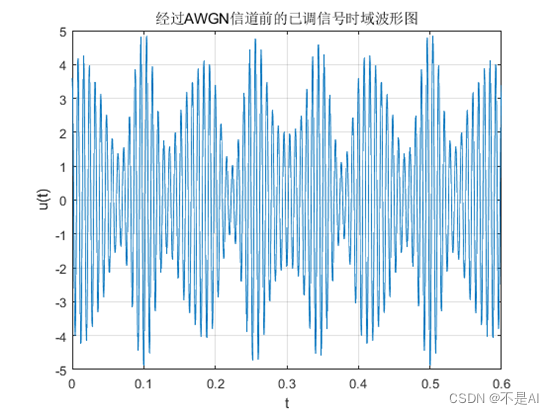
（2）、经过AWGN信道前的已调信号的频谱：

（3）、经过AWGN信道后的已调信号的时域波形图：

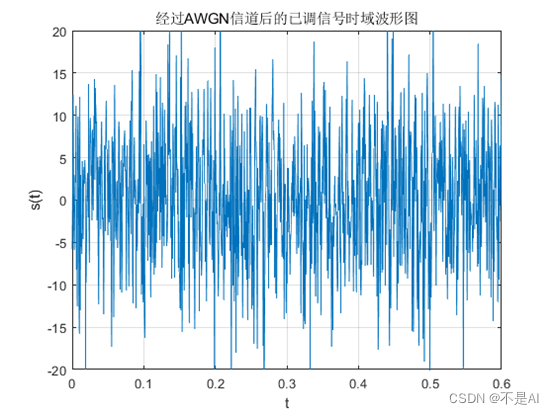
（4）、经过AWGN信道后的已调信号的频谱图：

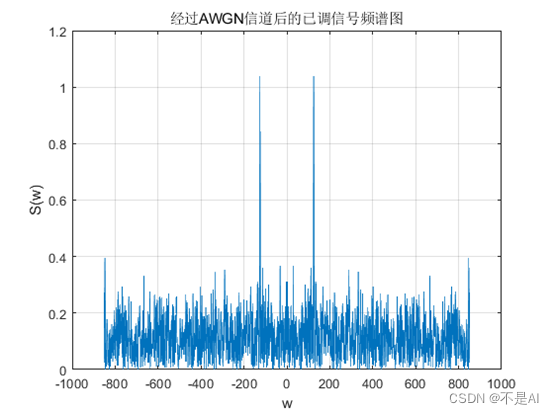
五、实验分析：
1、求离散时间信号傅里叶变换：

function [f, sf] = F(t, st)
%利用fft,fftshift定义函数F计算信号的傅里叶变换
%t-离散时间
%st-离散信号
dt = t(2) - t(1); %时间分辨率
T = t(end);
df = 1 / T; %频率分辨率
N = length(st); %离散傅里叶变换长度
f = -N / 2 * df : df : N / 2 * df - df;
sf = fft(st);
sf = T / N * fftshift(sf);

2、求信号平均功率：

function p = power_x(x)
%x:输入信号
%p:返回信号的x功率
p = (norm(x) .^ 2) ./ length(x);

3、求信号等效带宽：

function [Bw_eq] = signalband(sf, df, T)
%计算信号等效带宽
%sf:信号频谱
%df:频谱分辨率
%T:信号持续时间
sf_max = max(abs(sf));
Bw_eq = sum(abs(sf) .^ 2) * df / T / sf_max .^ 2;

4、序列的傅里叶变换

function [M, m, df] = fftseq(m, ts, df)
 
fs = 1 / ts;
if nargin == 2
    n1 = 0;
else
    n1 = fs / df;
end
n2 = length(m);
n = 2 ^ (max(nextpow2(n1), nextpow2(n2)));
M = fft(m, n);
m = [m, zeros(1, n - n2)];
df = fs / n;

5、信号从时域转换到频域

function [M, m, df1, f]=T2F(m, ts, df, fs)
%-----------------输入参数
%m: 信号
%ts: 系统时域采样间隔
%df: 所需的频率分辨率
%fs: 系统采样频率
 
%-----------------输出参数
%M: 傅里叶变换后的频谱序列
%m: 输入信号参与过傅里叶变换后对应的序列，补零后的输入信号，长度与M，f相同
%df1: 返回的频率分辨率
%f: 与M相对应的频率序列
[M, m, df1] = fftseq(m, ts, df);
f = [0 : df1 : df1 * (length(m) - 1)] - fs / 2;  %频率向量
M = M / fs;