MATLAB|基于线性准则的考虑风力发电不确定性的分布鲁棒优化机组组合

?

目录

?

主要内容???

??部分程序???

???结果一览???

下载链接

主要内容???

该模型通过定义一系列风电分布的模糊性集来捕捉风电的不确定性，并在最坏情况分布下最小化预期总成本。与随机规划相比，该方法对精确概率分布数据的依赖性较小。该方法的性能也优于传统的鲁棒优化方法，因为它可以将一些分布信息纳入模糊集，从而产生保守性较低的结果。为了便于计算，假设经济调度决策与不确定参数和描述风力发电分布特征的辅助随机变量亲和依赖，采用线性决策规则逼近的方法处理等待决策。程序需要matlab+cplex进行求解。

??部分程序???

%% 确定性优化结果
clc
close all
clear all
% A Benchmark Case of Optimal Recourse Under Wind Power Uncertainty
D = 320; %MW         % demand
what = 60;           % mean wind output平均风功率
V = 3000; % $/MW      % penalty cost for load loss失负荷惩罚
a = 3;   % $/MW 发电成本系数
b = 30;  % $
% v为预测误差
?
x = binvar(1); % 机组启停机
p = sdpvar(1); % 机组出力
l = sdpvar(1);% 失负荷
% 不确定性变量
ResultP = [];
ResultQ = [];
i= 1;
for v = -50 :10 :100
    
Q =  b * x + a * p +V * l;
constrains = [ p >= 20*x;
               p <= 300*x ;
               p + l == D - what - v;
               l >= 0 ;];
opt = sdpsettings('verbose',1,'solver','cplex');
?
result = optimize(constrains,Q,opt); % 主问题求解         
ResultP(i) = value(p);
ResultQ(i) = value(Q);
i = i+1;
end
%
?
% hold on 
% bar(ResultQ)
% ylim([120,320])
xticklabels(-50:10:100)
?
clearvars -except ResultP
?
?
?
?
%% 线性近似求解
%% 模糊集参数
v = sdpvar;
u = sdpvar;
[A,b]=  FuzzyMatrix();
% A*[v;u] <=b;
% v,u 无约束
?
?
?
%% 机组相关变量
x = binvar(1);  % 一阶段
% 二阶段 
p0 = sdpvar;
p1 = sdpvar;
l0 = sdpvar;
l1 = sdpvar;
?
% 相关约束
?
%% p >= 20*x                  ( 任意 v,u）1
% min( [p1,0]*[v;u]) >= 20*x - p0
% A[v;u] <=b
% v,u  无约束
?
% 左边转换 
DualSize1 = sdpvar(size(A,1),1,'full');          % 对偶变量
DualSize1Constrains = [ A' * DualSize1 == [p1;0];                       
                        DualSize1 <= -0.0009 ;
                        b' *   DualSize1 >= 20 * x - p0;  ];                 % 目标函数    
               
?
?
?
%% p <= 300 * x               ( 任意 v,u）2
% -p >= -300 * x
% min( -p0 - p1 * v - 0 *u ) >=-300 * x
% A[v;u] <=b
% v,u  无约束
?
% 左边转换
DualSize2 = sdpvar(size(A,1),1,'full');          % 对偶变量
DualSize2Constrains = [ A' * DualSize2 == [-p1;0];                       
                        DualSize2 <= 0;
                        b' *   DualSize2 >= -300 * x + p0;  ];                 % 目标函数 
?
?
?
?
?
%% p+l = 260 - v              ( 任意 v,u）3
% p+l >= 260-v;
% p0 + p1*v +0*u + l0 + l1*v + 0*u +v >=260；
% min( p1*v +0*u  + l1*v + 0*u +v) >= 260 - p0 - l0;
% A[v;u] <=b
% v,u  无约束
?
% 左边转换
DualSize3 = sdpvar(size(A,1),1,'full');          % 对偶变量
DualSize3Constrains = [ A' * DualSize3 == [p1+l1+1;0];                       
                        DualSize3 <= 0;
                        b' *   DualSize3 >= 260-p0-l0;  ];                 % 目标函数 
?

???结果一览???

运行结果

原文结果图

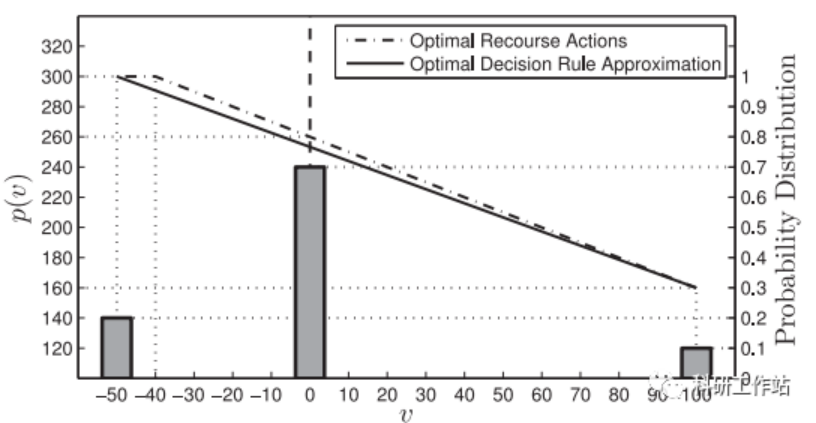
下载链接