Lowest Common Ancestor of a Binary Search Tree

Problem

Given a binary search tree (BST), find the lowest common ancestor (LCA) node of two given nodes in the BST.

According to the?definition of LCA on Wikipedia: “The lowest common ancestor is defined between two nodes?p?and?q?as the lowest node in?T?that has both?p?and?q?as descendants (where we allow?a node to be a descendant of itself).”

Example 1:

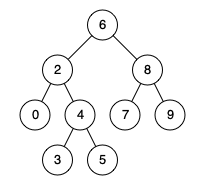
Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
Output: 6
Explanation: The LCA of nodes 2 and 8 is 6.

Example 2:

Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
Output: 2
Explanation: The LCA of nodes 2 and 4 is 2, since a node can be a descendant of itself according to the LCA definition.

Example 3:

Input: root = [2,1], p = 2, q = 1
Output: 2

Intuition

The goal is to find the lowest common ancestor (LCA) of two given nodes in a binary search tree (BST). The intuition is to exploit the properties of a BST, where nodes in the left subtree are smaller than the root, and nodes in the right subtree are larger than the root. By comparing the values of the nodes p and q with the value of the current root, we can determine the location of the LCA.

Approach

Traversal:

Start with the root of the BST.
While traversing the tree:
If both p and q are greater than the current root's value, move to the right subtree.
If both p and q are smaller than the current root's value, move to the left subtree.
If the current root's value is between p and q, or if it is equal to either p or q, then the current root is the LCA. Return the current root.
Return Result:

Return the final result, which is the lowest common ancestor of p and q.

Complexity

• Time complexity:

The time complexity is O(h), where h is the height of the binary search tree. In the average case, for a balanced BST, the height is O(log n), making the time complexity O(log n). However, in the worst case of an unbalanced tree, the height could be O(n), resulting in a time complexity of O(n).

• Space complexity:

The space complexity is O(1) since no additional data structures are used that scale with the input size. The algorithm uses a constant amount of space to store the current root and temporary variables.

Code

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
        while root:
            if root.val < p.val and root.val < q.val:
                root = root.right
            
            elif root.val > p.val and root.val > q.val:
                root = root.left
            
            else:
                return root
        return None