案例系列:电信客户流失_生存分析Survival Analysis
生存分析应该是每个数据科学家工具箱的一部分 - 但除非您从事临床研究,否则可能不是。它起源于医学统计学(从术语上可以看出),但应用范围更广。在本集中,我们将讨论何时以及为什么应该考虑使用生存分析,并展示如何将其应用于不同的问题 - 包括流失和客户生命周期价值。我们将使用lifelines - 一个出色的Python包,将传统方法引入现代机器学习。
# 安装lifelines库
! pip install lifelines
Collecting lifelines
Downloading lifelines-0.27.3-py3-none-any.whl (349 kB)
|████████████████████████████████| 349 kB 596 kB/s
[?25hCollecting formulaic>=0.2.2
Downloading formulaic-0.5.2-py3-none-any.whl (77 kB)
|████████████████████████████████| 77 kB 3.1 MB/s
[?25hCollecting autograd>=1.3
Downloading autograd-1.5-py3-none-any.whl (48 kB)
|████████████████████████████████| 48 kB 3.4 MB/s
[?25hRequirement already satisfied: pandas>=1.0.0 in /opt/conda/lib/python3.7/site-packages (from lifelines) (1.3.4)
Collecting autograd-gamma>=0.3
Downloading autograd-gamma-0.5.0.tar.gz (4.0 kB)
Preparing metadata (setup.py) ... [?25l- done
[?25hRequirement already satisfied: matplotlib>=3.0 in /opt/conda/lib/python3.7/site-packages (from lifelines) (3.5.0)
Requirement already satisfied: numpy>=1.14.0 in /opt/conda/lib/python3.7/site-packages (from lifelines) (1.19.5)
Requirement already satisfied: scipy>=1.2.0 in /opt/conda/lib/python3.7/site-packages (from lifelines) (1.7.2)
Requirement already satisfied: future>=0.15.2 in /opt/conda/lib/python3.7/site-packages (from autograd>=1.3->lifelines) (0.18.2)
Requirement already satisfied: wrapt>=1.0 in /opt/conda/lib/python3.7/site-packages (from formulaic>=0.2.2->lifelines) (1.13.3)
Collecting astor>=0.8
Downloading astor-0.8.1-py2.py3-none-any.whl (27 kB)
Requirement already satisfied: cached-property>=1.3.0 in /opt/conda/lib/python3.7/site-packages (from formulaic>=0.2.2->lifelines) (1.5.2)
Collecting interface-meta>=1.2.0
Downloading interface_meta-1.3.0-py3-none-any.whl (14 kB)
Collecting graphlib-backport>=1.0.0
Downloading graphlib_backport-1.0.3-py3-none-any.whl (5.1 kB)
Collecting typing-extensions>=4.2.0
Downloading typing_extensions-4.3.0-py3-none-any.whl (25 kB)
Requirement already satisfied: kiwisolver>=1.0.1 in /opt/conda/lib/python3.7/site-packages (from matplotlib>=3.0->lifelines) (1.3.2)
Requirement already satisfied: pillow>=6.2.0 in /opt/conda/lib/python3.7/site-packages (from matplotlib>=3.0->lifelines) (8.2.0)
Requirement already satisfied: python-dateutil>=2.7 in /opt/conda/lib/python3.7/site-packages (from matplotlib>=3.0->lifelines) (2.8.0)
Requirement already satisfied: packaging>=20.0 in /opt/conda/lib/python3.7/site-packages (from matplotlib>=3.0->lifelines) (21.0)
Requirement already satisfied: pyparsing>=2.2.1 in /opt/conda/lib/python3.7/site-packages (from matplotlib>=3.0->lifelines) (3.0.6)
Requirement already satisfied: cycler>=0.10 in /opt/conda/lib/python3.7/site-packages (from matplotlib>=3.0->lifelines) (0.11.0)
Requirement already satisfied: fonttools>=4.22.0 in /opt/conda/lib/python3.7/site-packages (from matplotlib>=3.0->lifelines) (4.28.2)
Requirement already satisfied: setuptools-scm>=4 in /opt/conda/lib/python3.7/site-packages (from matplotlib>=3.0->lifelines) (6.3.2)
Requirement already satisfied: pytz>=2017.3 in /opt/conda/lib/python3.7/site-packages (from pandas>=1.0.0->lifelines) (2021.3)
Requirement already satisfied: six>=1.5 in /opt/conda/lib/python3.7/site-packages (from python-dateutil>=2.7->matplotlib>=3.0->lifelines) (1.16.0)
Requirement already satisfied: setuptools in /opt/conda/lib/python3.7/site-packages (from setuptools-scm>=4->matplotlib>=3.0->lifelines) (59.1.1)
Requirement already satisfied: tomli>=1.0.0 in /opt/conda/lib/python3.7/site-packages (from setuptools-scm>=4->matplotlib>=3.0->lifelines) (1.2.2)
Building wheels for collected packages: autograd-gamma
Building wheel for autograd-gamma (setup.py) ... [?25l- \ done
[?25h Created wheel for autograd-gamma: filename=autograd_gamma-0.5.0-py3-none-any.whl size=4049 sha256=6bb62f817548a4b4fac98ae182f4905318553653538de2f3676694fb798b42de
Stored in directory: /root/.cache/pip/wheels/9f/01/ee/1331593abb5725ff7d8c1333aee93a50a1c29d6ddda9665c9f
Successfully built autograd-gamma
Installing collected packages: typing-extensions, interface-meta, graphlib-backport, autograd, astor, formulaic, autograd-gamma, lifelines
Attempting uninstall: typing-extensions
Found existing installation: typing-extensions 3.10.0.2
Uninstalling typing-extensions-3.10.0.2:
Successfully uninstalled typing-extensions-3.10.0.2
[31mERROR: pip's dependency resolver does not currently take into account all the packages that are installed. This behaviour is the source of the following dependency conflicts.
tensorflow-io 0.21.0 requires tensorflow-io-gcs-filesystem==0.21.0, which is not installed.
explainable-ai-sdk 1.3.2 requires xai-image-widget, which is not installed.
thinc 8.0.13 requires typing-extensions<4.0.0.0,>=3.7.4.1; python_version < "3.8", but you have typing-extensions 4.3.0 which is incompatible.
tensorflow 2.6.2 requires six~=1.15.0, but you have six 1.16.0 which is incompatible.
tensorflow 2.6.2 requires typing-extensions~=3.7.4, but you have typing-extensions 4.3.0 which is incompatible.
tensorflow 2.6.2 requires wrapt~=1.12.1, but you have wrapt 1.13.3 which is incompatible.
tensorflow-transform 1.4.0 requires absl-py<0.13,>=0.9, but you have absl-py 0.15.0 which is incompatible.
tensorflow-transform 1.4.0 requires pyarrow<6,>=1, but you have pyarrow 6.0.0 which is incompatible.
spacy 3.1.4 requires typing-extensions<4.0.0.0,>=3.7.4; python_version < "3.8", but you have typing-extensions 4.3.0 which is incompatible.
optax 0.1.0 requires typing-extensions~=3.10.0, but you have typing-extensions 4.3.0 which is incompatible.
flake8 4.0.1 requires importlib-metadata<4.3; python_version < "3.8", but you have importlib-metadata 4.8.2 which is incompatible.
arviz 0.11.4 requires typing-extensions<4,>=3.7.4.3, but you have typing-extensions 4.3.0 which is incompatible.
apache-beam 2.34.0 requires dill<0.3.2,>=0.3.1.1, but you have dill 0.3.4 which is incompatible.
apache-beam 2.34.0 requires httplib2<0.20.0,>=0.8, but you have httplib2 0.20.2 which is incompatible.
apache-beam 2.34.0 requires pyarrow<6.0.0,>=0.15.1, but you have pyarrow 6.0.0 which is incompatible.
apache-beam 2.34.0 requires typing-extensions<4,>=3.7.0, but you have typing-extensions 4.3.0 which is incompatible.
aiobotocore 2.0.1 requires botocore<1.22.9,>=1.22.8, but you have botocore 1.23.15 which is incompatible.[0m
Successfully installed astor-0.8.1 autograd-1.5 autograd-gamma-0.5.0 formulaic-0.5.2 graphlib-backport-1.0.3 interface-meta-1.3.0 lifelines-0.27.3 typing-extensions-4.3.0
[33mWARNING: Running pip as the 'root' user can result in broken permissions and conflicting behaviour with the system package manager. It is recommended to use a virtual environment instead: https://pip.pypa.io/warnings/venv[0m
!pip install lifetimes
Collecting lifetimes
Downloading Lifetimes-0.11.3-py3-none-any.whl (584 kB)
|████████████████████████████████| 584 kB 597 kB/s
[?25hRequirement already satisfied: dill>=0.2.6 in /opt/conda/lib/python3.7/site-packages (from lifetimes) (0.3.4)
Requirement already satisfied: pandas>=0.24.0 in /opt/conda/lib/python3.7/site-packages (from lifetimes) (1.3.4)
Requirement already satisfied: autograd>=1.2.0 in /opt/conda/lib/python3.7/site-packages (from lifetimes) (1.5)
Requirement already satisfied: scipy>=1.0.0 in /opt/conda/lib/python3.7/site-packages (from lifetimes) (1.7.2)
Requirement already satisfied: numpy>=1.10.0 in /opt/conda/lib/python3.7/site-packages (from lifetimes) (1.19.5)
Requirement already satisfied: future>=0.15.2 in /opt/conda/lib/python3.7/site-packages (from autograd>=1.2.0->lifetimes) (0.18.2)
Requirement already satisfied: python-dateutil>=2.7.3 in /opt/conda/lib/python3.7/site-packages (from pandas>=0.24.0->lifetimes) (2.8.0)
Requirement already satisfied: pytz>=2017.3 in /opt/conda/lib/python3.7/site-packages (from pandas>=0.24.0->lifetimes) (2021.3)
Requirement already satisfied: six>=1.5 in /opt/conda/lib/python3.7/site-packages (from python-dateutil>=2.7.3->pandas>=0.24.0->lifetimes) (1.16.0)
Installing collected packages: lifetimes
Successfully installed lifetimes-0.11.3
[33mWARNING: Running pip as the 'root' user can result in broken permissions and conflicting behaviour with the system package manager. It is recommended to use a virtual environment instead: https://pip.pypa.io/warnings/venv[0m
# 安装pysurvival包
!pip install pysurvival
Collecting pysurvival
Downloading pysurvival-0.1.2.tar.gz (4.7 MB)
|████████████████████████████████| 4.7 MB 580 kB/s
[?25h Preparing metadata (setup.py) ... [?25l- \ done
[?25hRequirement already satisfied: matplotlib in /opt/conda/lib/python3.7/site-packages (from pysurvival) (3.5.0)
Requirement already satisfied: numpy in /opt/conda/lib/python3.7/site-packages (from pysurvival) (1.19.5)
Requirement already satisfied: pandas in /opt/conda/lib/python3.7/site-packages (from pysurvival) (1.3.4)
Requirement already satisfied: pip in /opt/conda/lib/python3.7/site-packages (from pysurvival) (21.3.1)
Collecting progressbar
Downloading progressbar-2.5.tar.gz (10 kB)
Preparing metadata (setup.py) ... [?25l- done
[?25hRequirement already satisfied: pyarrow in /opt/conda/lib/python3.7/site-packages (from pysurvival) (6.0.0)
Requirement already satisfied: scikit-learn in /opt/conda/lib/python3.7/site-packages (from pysurvival) (0.23.2)
Requirement already satisfied: scipy in /opt/conda/lib/python3.7/site-packages (from pysurvival) (1.7.2)
Requirement already satisfied: sklearn in /opt/conda/lib/python3.7/site-packages (from pysurvival) (0.0)
Requirement already satisfied: torch in /opt/conda/lib/python3.7/site-packages (from pysurvival) (1.9.1+cpu)
Requirement already satisfied: setuptools-scm>=4 in /opt/conda/lib/python3.7/site-packages (from matplotlib->pysurvival) (6.3.2)
Requirement already satisfied: cycler>=0.10 in /opt/conda/lib/python3.7/site-packages (from matplotlib->pysurvival) (0.11.0)
Requirement already satisfied: python-dateutil>=2.7 in /opt/conda/lib/python3.7/site-packages (from matplotlib->pysurvival) (2.8.0)
Requirement already satisfied: fonttools>=4.22.0 in /opt/conda/lib/python3.7/site-packages (from matplotlib->pysurvival) (4.28.2)
Requirement already satisfied: kiwisolver>=1.0.1 in /opt/conda/lib/python3.7/site-packages (from matplotlib->pysurvival) (1.3.2)
Requirement already satisfied: packaging>=20.0 in /opt/conda/lib/python3.7/site-packages (from matplotlib->pysurvival) (21.0)
Requirement already satisfied: pillow>=6.2.0 in /opt/conda/lib/python3.7/site-packages (from matplotlib->pysurvival) (8.2.0)
Requirement already satisfied: pyparsing>=2.2.1 in /opt/conda/lib/python3.7/site-packages (from matplotlib->pysurvival) (3.0.6)
Requirement already satisfied: pytz>=2017.3 in /opt/conda/lib/python3.7/site-packages (from pandas->pysurvival) (2021.3)
Requirement already satisfied: threadpoolctl>=2.0.0 in /opt/conda/lib/python3.7/site-packages (from scikit-learn->pysurvival) (3.0.0)
Requirement already satisfied: joblib>=0.11 in /opt/conda/lib/python3.7/site-packages (from scikit-learn->pysurvival) (1.1.0)
Requirement already satisfied: typing-extensions in /opt/conda/lib/python3.7/site-packages (from torch->pysurvival) (4.3.0)
Requirement already satisfied: six>=1.5 in /opt/conda/lib/python3.7/site-packages (from python-dateutil>=2.7->matplotlib->pysurvival) (1.16.0)
Requirement already satisfied: setuptools in /opt/conda/lib/python3.7/site-packages (from setuptools-scm>=4->matplotlib->pysurvival) (59.1.1)
Requirement already satisfied: tomli>=1.0.0 in /opt/conda/lib/python3.7/site-packages (from setuptools-scm>=4->matplotlib->pysurvival) (1.2.2)
Building wheels for collected packages: pysurvival, progressbar
Building wheel for pysurvival (setup.py) ... [?25l- \ | / - \ | / - \ | / - \ | / - \ | / - \ | / - \ | / - \ | / - \ | / - \ | / - \ | / - \ | done
[?25h Created wheel for pysurvival: filename=pysurvival-0.1.2-cp37-cp37m-linux_x86_64.whl size=5329192 sha256=ff7a55a1567f73315cdf78b8074681bf0d6b5e09d0575d81674ef6263f18c4cf
Stored in directory: /root/.cache/pip/wheels/1a/63/e2/32273d765a4e2f4ccac69c8adf97425ca80bab5d0c8447f120
Building wheel for progressbar (setup.py) ... [?25l- \ done
[?25h Created wheel for progressbar: filename=progressbar-2.5-py3-none-any.whl size=12082 sha256=b6dbdf40db2521c37fcf6a79f76c36121cc6b056e450c9d8f99041c1d10ddde2
Stored in directory: /root/.cache/pip/wheels/f0/fd/1f/3e35ed57e94cd8ced38dd46771f1f0f94f65fec548659ed855
Successfully built pysurvival progressbar
Installing collected packages: progressbar, pysurvival
Successfully installed progressbar-2.5 pysurvival-0.1.2
[33mWARNING: Running pip as the 'root' user can result in broken permissions and conflicting behaviour with the system package manager. It is recommended to use a virtual environment instead: https://pip.pypa.io/warnings/venv[0m
# 导入必要的库
import numpy as np
import pandas as pd
import os
import pandas_datareader as web
import matplotlib.pyplot as plt
%matplotlib inline
# 设置绘图风格
plt.style.use('fivethirtyeight')
# 忽略警告信息
import warnings
warnings.simplefilter(action='ignore', category= FutureWarning)
# 定义一个名为CFG的类
class CFG:
# 设置种子为42
seed = 42
# 设置图像维度1为20
img_dim1 = 20
# 设置图像维度2为10
# 调整显示图形的参数
# 更新figure.figsize参数为CFG.img_dim1和CFG.img_dim2的值
plt.rcParams.update({'figure.figsize': (CFG.img_dim1,CFG.img_dim2)})
生存分析简介
到目前为止,我们主要看到的是时间序列,我们观察到了过去,我们知道发生了什么/何时 - 预测是基于这些信息的。但并不总是这样:
Q1:我们需要在观察到所有数据之前采取行动吗?
Q2:事件发生的时间是否重要?
# 创建一个二维数组S,大小为list1的长度乘以list2的长度
# 并将其转换为DataFrame格式,并设置行索引为list1,列索引为list2
list1 = ['P1', 'P2', 'P3', 'P4', 'P5']
list2 = ['2016','2017','2018','2019','2020','2021']
S = np.zeros((len(list1),len(list2)))
S = pd.DataFrame(S); S.index = list1; S.columns = list2
# 将S中的某些元素设置为1
S.loc['P1'][['2019','2020','2021']] = 1
S.loc['P3'][['2018','2019','2020','2021']] = 1
S.loc['P4'][['2021']] = 1
S.loc['P5'][['2020','2021']] = 1
# 将S的元素类型转换为整数类型
S = S.astype(int)
# 显示S的内容
display(S)
| 2016 | 2017 | 2018 | 2019 | 2020 | 2021 | |
|---|---|---|---|---|---|---|
| P1 | 0 | 0 | 0 | 1 | 1 | 1 |
| P2 | 0 | 0 | 0 | 0 | 0 | 0 |
| P3 | 0 | 0 | 1 | 1 | 1 | 1 |
| P4 | 0 | 0 | 0 | 0 | 0 | 1 |
| P5 | 0 | 0 | 0 | 0 | 1 | 1 |
2x YES ?? ? ?? \implies ? 使用生存分析:
-
一组处理时间事件的统计方法 → \rightarrow → 感兴趣的事件发生需要多长时间
-
我们必须在某个时间点关闭观察窗口,以完成我们的数据集并做出决策,
-
不能等待所有数据到位 → \rightarrow → 我们的一些数据将被截断
-
一些受试者尚未经历目标事件 ?? ? ?? \implies ? 我们只知道时间到事件至少持续一段时间。
-
结果具有事件和时间值
-
生存模型:预测 + 因果推断
-
在某个时间点上/之后事件周围的概率分布
-
各种因素对持续时间的贡献
-
摘要1:量化/可视化持续时间的分布 → \rightarrow → 期望/基线/阈值
-
摘要2:个体受试者的生存曲线 → \rightarrow → 优先考虑干预措施
生存分析可能是正确方法的不同使用案例如下所示(来源):

基本工具包
我们需要三个主要的构建模块来开始应用生存分析:
-
随机变量 T T T代表感兴趣事件的时间
-
生存函数 S t S_t St? - 事件在时间 t t t之后发生的概率
-
危险函数 h t h_t ht? - 瞬时风险
我们在下面简要讨论它们
事件时间
-
我们从表示感兴趣事件时间的随机变量 T T T开始(见上文)。
-
连续随机变量: [ 0 , ∞ ) [0, \infty) [0,∞) → \rightarrow → [ 0 , 1 ] [0,1] [0,1]
以图形形式表示(来源):

到目前为止一切顺利 - 但是生存分析的特殊之处在于截尾: ~ \sim ~生存分析的NA。当关于生存时间的信息不完整时,观测值被截尾:
-
我们不知道观测期后可能发生了什么,但是事件的缺失对风险是有信息的
-
被截尾的观测值对总风险有贡献
有三种类型的截尾:右截尾、左截尾和区间截尾:
右截尾
最常见的截尾类型:当观测期结束时,生存时间是不完整的
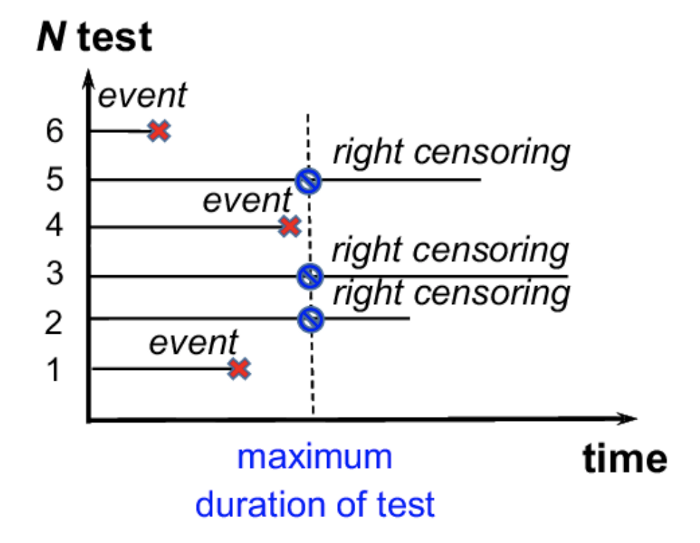
左截尾
左截尾发生在我们无法观测到事件发生的时间时

区间截尾
我们在 t 1 t_1 t1?和 t 2 t_2 t2?进行了测试 - 首先是负结果,然后是正结果 → \rightarrow → 我们只知道事件发生在 t 1 t_1 t1?和 t 2 t_2 t2?之间的某个时间点
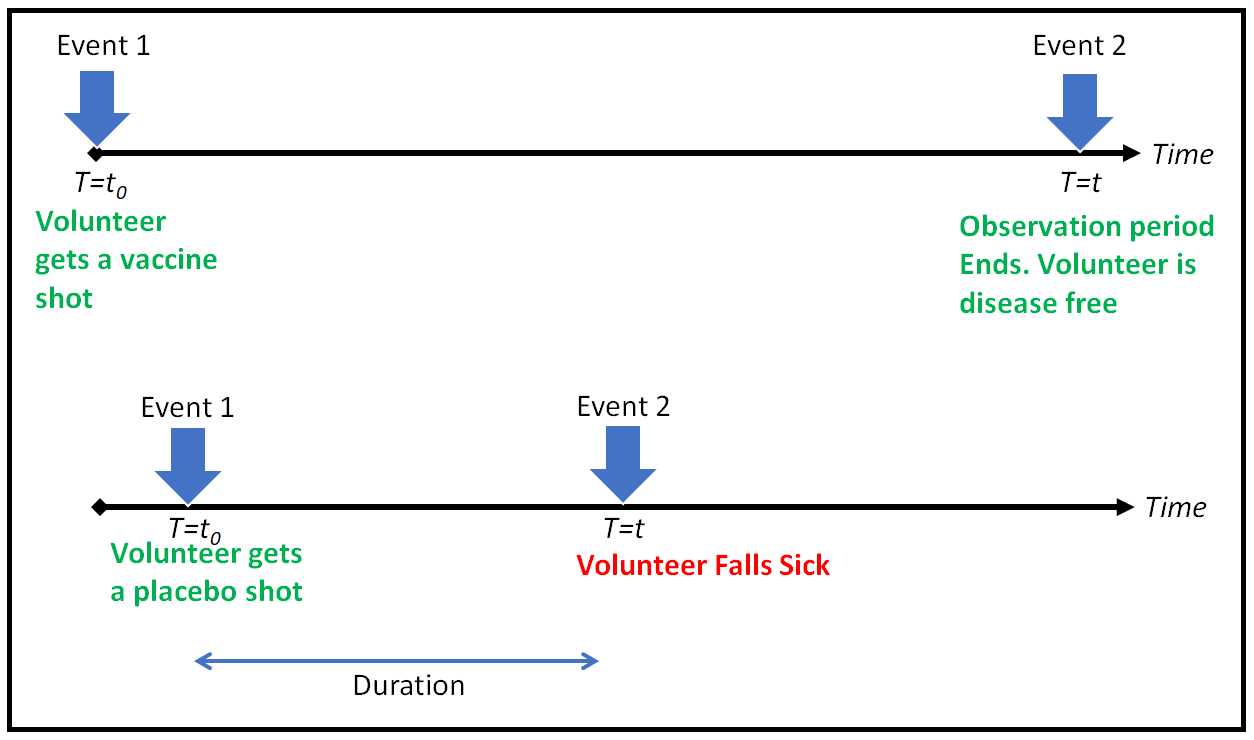
-
右截尾阻止了OLS类型的方法的使用 → \rightarrow → 错误是未知的
-
快速修复可能引入偏差
关于不同类型截尾的很好的总结可以在Wikipedia文章中找到。
生存函数
生存函数由以下公式给出:
\begin{equation}
S(t) = P(T > t)
\end{equation}
解释:在时间 t t t之前,事件不发生的概率。
KM估计器
Kaplan-Meier估计器:
-
生存函数的非参数估计
-
在存在截尾的情况下,对单个随机变量进行非负回归和密度估计
-
根据观察到的事件时间将估计分为多个步骤
\begin{equation}
\hat{S}(t) = \prod_{i: t_i \leq t} \left(1 - \frac{d_i}{n_i} \right)
\end{equation}
其中 n i n_i ni?是在时间点 t i t_i ti?处处于风险中的个体数量, d i d_i di?是在时间点 t i t_i ti?经历事件的个体数量。
假设在必要的理论介绍之后,您仍然在这里,让我们看看如何将生存分析应用于一个流失数据集(Kaggle数据集:https://www.kaggle.com/datasets/blastchar/telco-customer-churn)。
# 读取csv文件,存储到df中
df = pd.read_csv('../input/telco-customer-churn/WA_Fn-UseC_-Telco-Customer-Churn.csv')
# 将Churn列中的Yes转换为1,No转换为0,存储到churn列中
df['churn'] = [1 if x == 'Yes' else 0 for x in df['Churn']]
# 显示前3行数据
df.head(3)
| customerID | gender | SeniorCitizen | Partner | Dependents | tenure | PhoneService | MultipleLines | InternetService | OnlineSecurity | ... | TechSupport | StreamingTV | StreamingMovies | Contract | PaperlessBilling | PaymentMethod | MonthlyCharges | TotalCharges | Churn | churn | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 7590-VHVEG | Female | 0 | Yes | No | 1 | No | No phone service | DSL | No | ... | No | No | No | Month-to-month | Yes | Electronic check | 29.85 | 29.85 | No | 0 |
| 1 | 5575-GNVDE | Male | 0 | No | No | 34 | Yes | No | DSL | Yes | ... | No | No | No | One year | No | Mailed check | 56.95 | 1889.5 | No | 0 |
| 2 | 3668-QPYBK | Male | 0 | No | No | 2 | Yes | No | DSL | Yes | ... | No | No | No | Month-to-month | Yes | Mailed check | 53.85 | 108.15 | Yes | 1 |
3 rows × 22 columns
# 导入所需的库
# 我们只需要基本模型中的时间到事件和流失标志
from lifelines import KaplanMeierFitter
# 从数据框中获取时间到事件和流失标志
T = df['tenure'] # 单位为月
E = df['churn']
# 创建Kaplan-Meier拟合器对象
kmf = KaplanMeierFitter()
# 对时间到事件和流失标志进行拟合
kmf.fit(T, event_observed=E)
# 绘制Kaplan-Meier曲线,同时显示风险人数
kmf.plot(at_risk_counts=True)
# 设置图表标题
plt.title('Kaplan-Meier曲线');

Kaplan-Meier估计可以像这样用于获取人口的一般概念:
-
估计的 S ^ \hat{S} S^是整个人口的阶梯函数
-
x轴:月份的任期,y轴:在该时间点之前客户未流失的概率
-
置信区间:格林伍德指数公式
如果我们想要更深入地了解人口子集(=分类特征的级别)的行为,该怎么办?
# 在画布上创建一个子图
ax = plt.subplot(111)
# 创建KaplanMeierFitter对象
kmf = KaplanMeierFitter()
# 遍历数据集中的每种支付方式
for payment_method in df['PaymentMethod'].unique():
# 获取当前支付方式的数据
flag = df['PaymentMethod'] == payment_method
# 使用当前支付方式的数据拟合Kaplan-Meier曲线
kmf.fit(T[flag], event_observed = E[flag], label = payment_method)
# 在子图上绘制当前支付方式的Kaplan-Meier曲线
kmf.plot(ax=ax)
# 设置图表标题
plt.title("Survival curves by payment method");
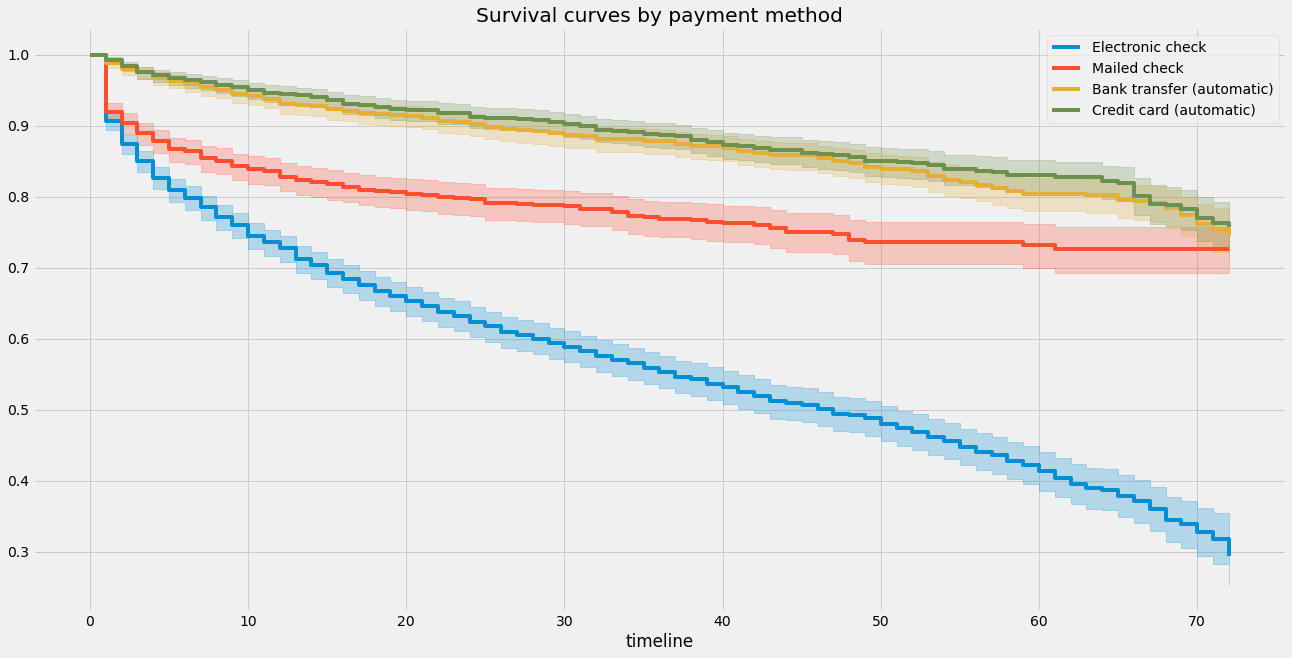
虽然很简单,但Kaplan-Meier估计器使我们能够解决EDA类型的问题-例如,我们可以使用logrank测试测试两个组是否具有不同的生存特征:
# 导入所需的函数
from lifelines.statistics import logrank_test, pairwise_logrank_test
# 创建一个布尔数组,用于判断是否为信用卡支付方式
credit_card_flag = df['PaymentMethod'] == 'Credit card (automatic)'
# 创建一个布尔数组,用于判断是否为银行转账支付方式
bank_transfer_flag = df['PaymentMethod'] == 'Bank transfer (automatic)'
# 使用logrank_test函数进行生存分析的对比检验,比较信用卡支付方式和银行转账支付方式的生存时间
# T[credit_card_flag]表示信用卡支付方式的生存时间数据
# T[bank_transfer_flag]表示银行转账支付方式的生存时间数据
# E[credit_card_flag]表示信用卡支付方式的生存状态数据(是否发生事件)
# E[bank_transfer_flag]表示银行转账支付方式的生存状态数据(是否发生事件)
results = logrank_test(T[credit_card_flag], T[bank_transfer_flag], E[credit_card_flag], E[bank_transfer_flag])
# 打印生存分析的对比检验结果的摘要信息
results.print_summary()
| t_0 | -1 |
|---|---|
| null_distribution | chi squared |
| degrees_of_freedom | 1 |
| test_name | logrank_test |
| test_statistic | p | -log2(p) | |
|---|---|---|---|
| 0 | 0.87 | 0.35 | 1.51 |
没有拒绝零假设(生存曲线相同)。那么比较所有组合呢?
# 使用pairwise_logrank_test函数计算生存分析的对数秩检验
# 参数df['tenure']表示生存时间,df['PaymentMethod']表示支付方式,df['churn']表示是否流失
results = lifelines.statistics.pairwise_logrank_test(df['tenure'], df['PaymentMethod'], df['churn'])
# 打印对数秩检验的结果摘要
results.print_summary()
| t_0 | -1 |
|---|---|
| null_distribution | chi squared |
| degrees_of_freedom | 1 |
| test_name | logrank_test |
| test_statistic | p | -log2(p) | ||
|---|---|---|---|---|
| Bank transfer (automatic) | Credit card (automatic) | 0.87 | 0.35 | 1.51 |
| Electronic check | 510.04 | <0.005 | 372.74 | |
| Mailed check | 51.07 | <0.005 | 40.03 | |
| Credit card (automatic) | Electronic check | 539.74 | <0.005 | 394.21 |
| Mailed check | 64.82 | <0.005 | 50.11 | |
| Electronic check | Mailed check | 152.46 | <0.005 | 113.93 |
K-M总结:
- (+) 灵活,假设最少
- (+) 快速
- (-) 没有考虑协变量 → \rightarrow → 预测 😦
- (-) 不平滑
我们能做得更好吗?
风险函数:
\begin{equation}
\lambda(t) = -\frac{S^{'}(t)}{S(t)}
\end{equation}
累积风险率:
\begin{equation}
\Lambda(t) = \int_0^t \lambda(s) ds = -\log S(t)
\end{equation}
累积风险率的Nelson-Aalen估计器:
\begin{equation}
\hat{\lambda}(t) = \sum_{i: t_i \leq t} \frac{d_i}{n_i}
\end{equation}
-
由于解释性较差而不太流行
-
作为Cox回归的构建模块很有用
-
测量累积风险在 t t t之前的总量
-
直观理解:如果不吸收(死亡+复活,故障+修复),预期事件数量
使用lifelines:
# 导入NelsonAalenFitter类
from lifelines import NelsonAalenFitter
# 创建一个NelsonAalenFitter对象
naf = NelsonAalenFitter()
# 使用fit方法拟合数据
# T表示时间数据,E表示事件观察数据
naf.fit(T, event_observed=E)
# 使用plot方法绘制累积风险函数图
# at_risk_counts参数表示是否显示在风险集合中的个体数量
naf.plot(at_risk_counts=True)
# 设置图表标题为'累积风险函数'
plt.title('Cumulative hazard function')
Text(0.5, 1.0, 'Cumulative hazard function')

# 在画布上创建一个子图
ax = plt.subplot(111)
# 创建一个NelsonAalenFitter对象
naf = NelsonAalenFitter()
# 遍历数据集中的每种支付方式
for payment_method in df['PaymentMethod'].unique():
# 创建一个布尔型Series,用于筛选出当前支付方式的数据
flag = df['PaymentMethod'] == payment_method
# 使用筛选后的数据拟合NelsonAalenFitter模型,并为该支付方式添加标签
naf.fit(T[flag], event_observed=E[flag], label=payment_method)
# 在子图上绘制累积风险函数曲线
naf.plot(ax=ax)
# 设置图表标题
plt.title('Cumulative hazard functions by payment method')
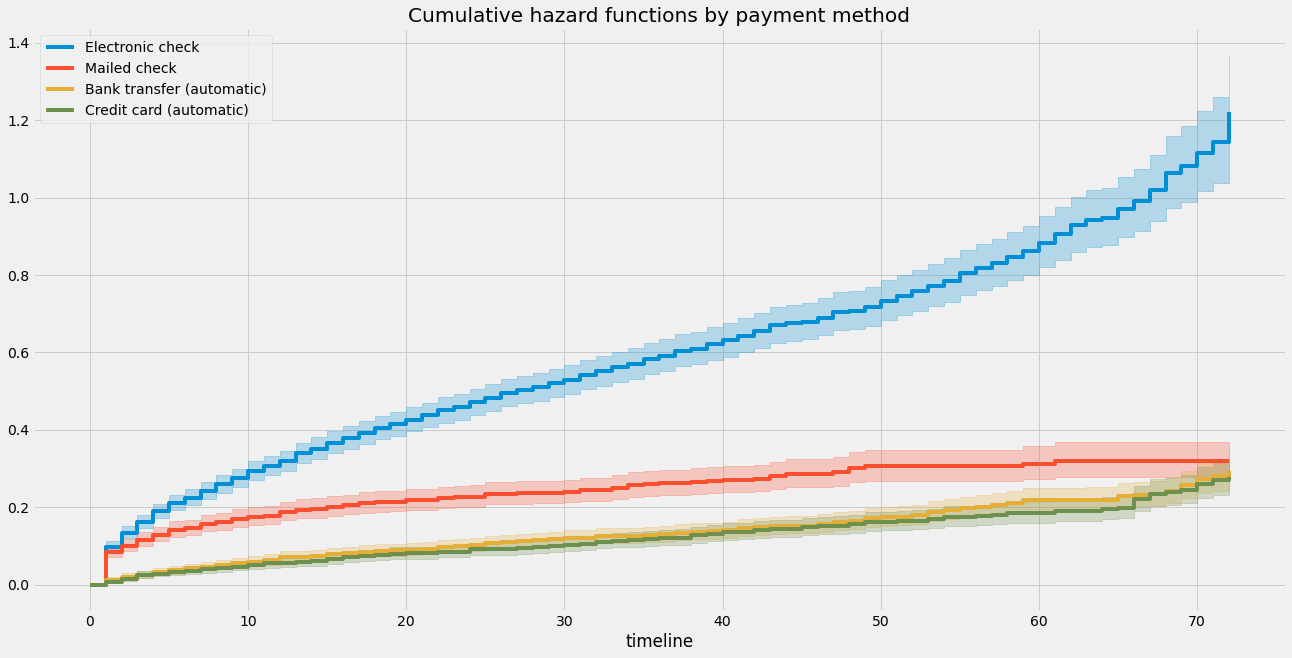
Cox回归
Cox比例风险模型由风险率关系定义:
\begin{equation}
\lambda(t) = \lambda_0(t) \exp \left( X^T \beta \right)
\end{equation}
- 协变量对风险率有乘法效应
- 效应在时间上是恒定的
- 总体基线风险 λ 0 \lambda_0 λ0?是时间不变的
- 失败时间是(条件)独立的
- λ 0 ( t ) \lambda_0(t) λ0?(t) - 基线风险
- 系数的符号 → \rightarrow →共单调
- 适用于右侧截尾数据
# 处理数据以适用于Cox模型
id_col = df['customerID'] # 获取顾客ID列
df.drop(['customerID', 'TotalCharges'], axis=1, inplace=True) # 删除顾客ID和总费用列
df = df[['gender', 'SeniorCitizen', 'Partner', 'tenure', 'churn', 'PhoneService', 'OnlineSecurity', 'Contract']] # 选择需要的列
df = pd.get_dummies(df, drop_first=True) # 对分类变量进行独热编码
# 将数据集分为训练集和测试集
df_train, df_test = df.iloc[:-10], df.iloc[-10:]
from lifelines import CoxPHFitter # 导入CoxPHFitter模型
cph = CoxPHFitter() # 创建CoxPHFitter对象
cph.fit(df_train, duration_col='tenure', event_col='churn') # 使用训练集拟合模型,设置生存时间列为tenure,事件列为churn
<lifelines.CoxPHFitter: fitted with 7033 total observations, 5166 right-censored observations>
性能的Cox模型 → \rightarrow → 一种生存模型的一致性指数 C-index ≈ \approx ≈ 时间特定ROC下面积的加权平均。
直觉:
-
C-index衡量判别能力
-
只评估排名:模型是否预测了与实际发生相同的流失顺序?
-
不受值(持续时间)的影响
-
对于右侧截尾数据是必要的恶。
# 打印模型的摘要信息,包括系数、指数化系数、指数化系数的下限和上限、z值和p值
cph.print_summary(columns=["coef","exp(coef)","exp(coef) lower 95%","exp(coef) upper 95%", "z", "p"], decimals=3)
| model | lifelines.CoxPHFitter |
|---|---|
| duration col | 'tenure' |
| event col | 'churn' |
| baseline estimation | breslow |
| number of observations | 7033 |
| number of events observed | 1867 |
| partial log-likelihood | -14141.867 |
| time fit was run | 2022-09-30 12:27:47 UTC |
| coef | exp(coef) | exp(coef) lower 95% | exp(coef) upper 95% | z | p | |
|---|---|---|---|---|---|---|
| SeniorCitizen | -0.034 | 0.966 | 0.869 | 1.075 | -0.633 | 0.527 |
| gender_Male | -0.056 | 0.945 | 0.863 | 1.035 | -1.218 | 0.223 |
| Partner_Yes | -0.615 | 0.541 | 0.490 | 0.596 | -12.341 | <0.0005 |
| PhoneService_Yes | 0.169 | 1.184 | 1.011 | 1.388 | 2.092 | 0.036 |
| OnlineSecurity_No internet service | -0.747 | 0.474 | 0.389 | 0.577 | -7.411 | <0.0005 |
| OnlineSecurity_Yes | -0.786 | 0.456 | 0.401 | 0.518 | -12.026 | <0.0005 |
| Contract_One year | -1.966 | 0.140 | 0.118 | 0.165 | -23.072 | <0.0005 |
| Contract_Two year | -3.774 | 0.023 | 0.017 | 0.031 | -23.470 | <0.0005 |
| Concordance | 0.829 |
|---|---|
| Partial AIC | 28299.733 |
| log-likelihood ratio test | 2985.035 on 8 df |
| -log2(p) of ll-ratio test | inf |
# 使用cph对象的plot()方法绘制风险因素的图表
cph.plot()
<AxesSubplot:xlabel='log(HR) (95% CI)'>

Prediction of individual survival curve generated by Cox model.
# 调用cph对象的predict_survival_function方法,对df_test进行生存函数预测。
cph.predict_survival_function(df_test)
| 7033 | 7034 | 7035 | 7036 | 7037 | 7038 | 7039 | 7040 | 7041 | 7042 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.0 | 1.000000 | 1.000000 | 1.000000 | 1.000000 | 1.000000 | 1.000000 | 1.000000 | 1.000000 | 1.000000 | 1.000000 |
| 1.0 | 0.873556 | 0.936883 | 0.873556 | 0.983238 | 0.998446 | 0.995348 | 0.989235 | 0.970676 | 0.931816 | 0.998586 |
| 2.0 | 0.828889 | 0.913465 | 0.828889 | 0.976805 | 0.997843 | 0.993548 | 0.985087 | 0.959523 | 0.906614 | 0.998038 |
| 3.0 | 0.793657 | 0.894529 | 0.793657 | 0.971514 | 0.997344 | 0.992060 | 0.981667 | 0.950391 | 0.886274 | 0.997584 |
| 4.0 | 0.762054 | 0.877169 | 0.762054 | 0.966590 | 0.996878 | 0.990671 | 0.978478 | 0.941926 | 0.867659 | 0.997160 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 68.0 | 0.029101 | 0.181620 | 0.029101 | 0.642557 | 0.960121 | 0.885149 | 0.753378 | 0.458987 | 0.157595 | 0.963662 |
| 69.0 | 0.018944 | 0.147654 | 0.018944 | 0.608972 | 0.955390 | 0.872138 | 0.727923 | 0.417591 | 0.125934 | 0.959343 |
| 70.0 | 0.008402 | 0.099758 | 0.008402 | 0.550100 | 0.946494 | 0.848020 | 0.682047 | 0.349148 | 0.082354 | 0.951215 |
| 71.0 | 0.004505 | 0.073856 | 0.004505 | 0.508849 | 0.939730 | 0.829981 | 0.648844 | 0.304374 | 0.059465 | 0.945030 |
| 72.0 | 0.001159 | 0.038381 | 0.001159 | 0.429420 | 0.925170 | 0.792023 | 0.582034 | 0.225754 | 0.029265 | 0.931703 |
73 rows × 10 columns
# 使用cph模型对测试数据进行生存概率预测,并绘制生存曲线图
# cph是一个已经训练好的Cox比例风险模型
# predict_survival_function函数用于预测生存概率函数
# df_test是测试数据集
# plot函数用于绘制生存曲线图
cph.predict_survival_function(df_test).plot()
<AxesSubplot:>
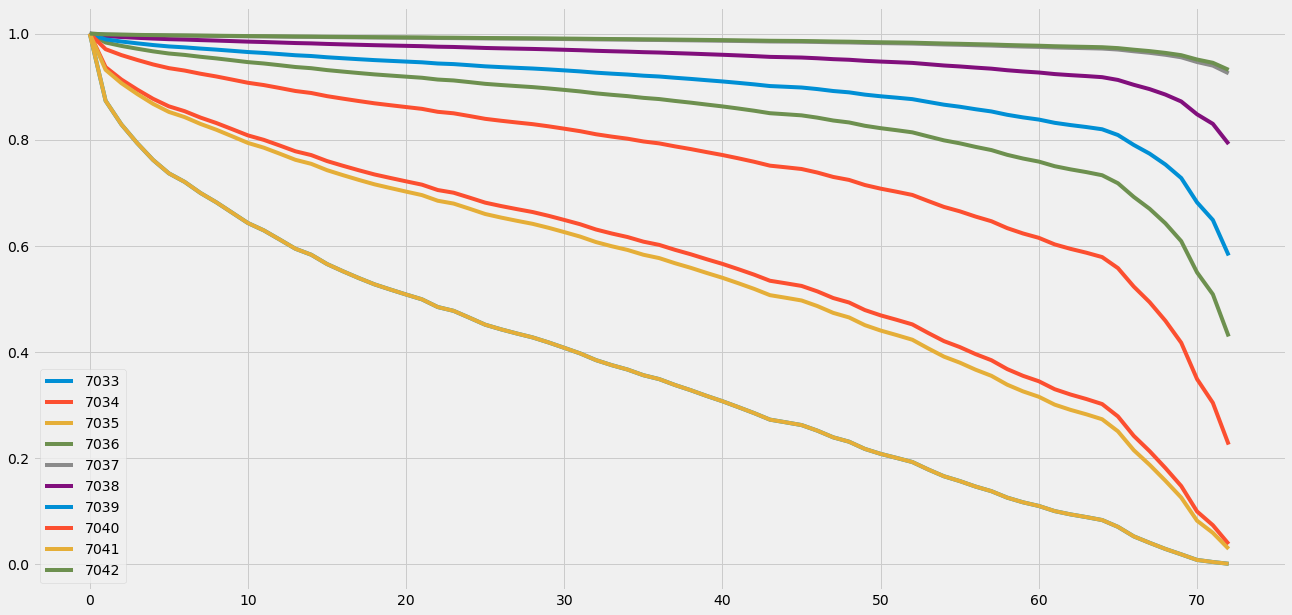
我们还可以放大诊断结果:
# 绘制指定协变量('Contract_Two year')对结果的部分效应图
cph.plot_partial_effects_on_outcome(covariates='Contract_Two year', values=[0, 1])
<AxesSubplot:>
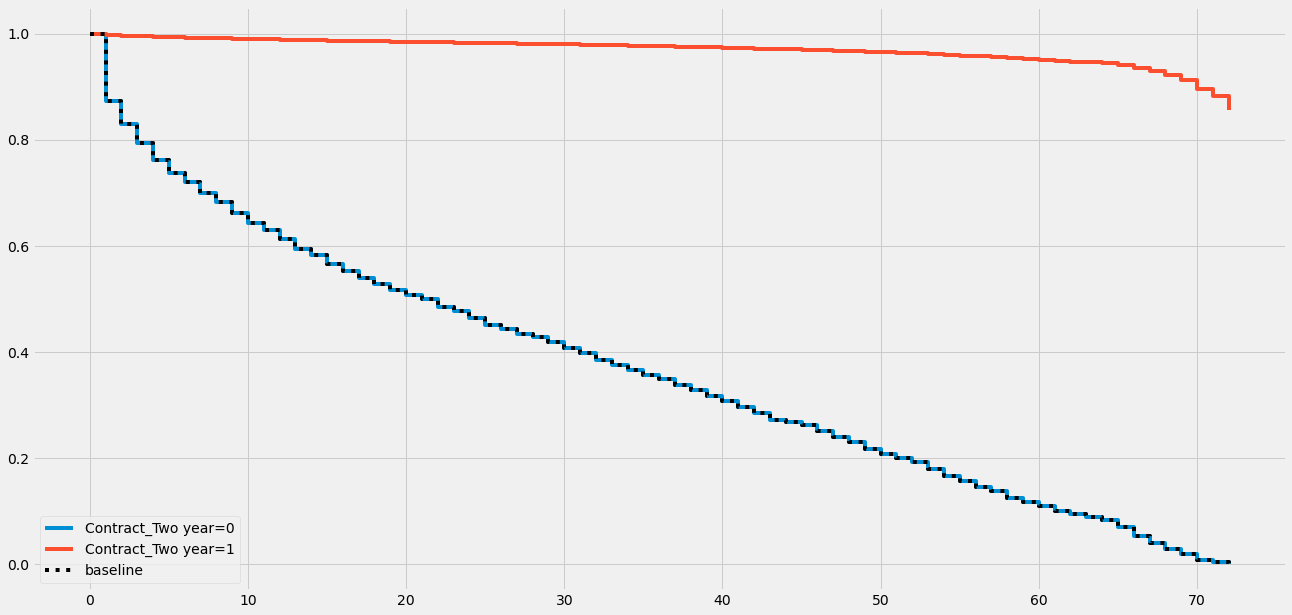
生存森林
我们从一个简单的非参数生存函数估计器开始,然后转向风险率,然后是后者的(对数)线性模型。逻辑上的下一步是什么?树 - 更准确地说,随机森林 + 生存分析 = 条件生存森林。
-
与随机森林相比的额外困难:数据被截断
-
ConditionalSurvivalForestModel通过添加事件列(是否被截断)来处理它 -
时间向量 T = m i n ( t , c ) T = min(t, c) T=min(t,c) ,其中 t 表示事件时间,c 表示截断时间
-
生存模型预测感兴趣事件在时间 t 发生的概率。
# 导入所需的库和模块
from pysurvival.datasets import Dataset # 导入数据集模块
from pysurvival.utils.display import correlation_matrix, compare_to_actual, integrated_brier_score, create_risk_groups # 导入显示相关性矩阵、与实际值比较、综合Brier分数、创建风险组的模块
from pysurvival.utils.metrics import concordance_index # 导入一致性指数模块
from pysurvival.models.survival_forest import ConditionalSurvivalForestModel # 导入条件生存森林模型模块
# 创建一个特征列表,包含除了'tenure'和'churn'以外的所有列名
features = [f for f in df_train.columns if f not in ['tenure', 'churn']]
# 定义时间列名和事件列名
time_column = 'tenure'
event_column = 'churn'
# 将数据集分为训练集和测试集,训练集包含除了最后10行以外的所有行,测试集包含最后10行
df_train, df_test = df.iloc[:-10], df.iloc[-10:]
# 从训练集和测试集中提取特征数据
X_train, X_test = df_train[features], df_test[features]
# 从训练集和测试集中提取时间数据
T_train, T_test = df_train[time_column], df_test[time_column]
# 从训练集和测试集中提取事件数据
E_train, E_test = df_train[event_column], df_test[event_column]
适配模型:
# 创建一个ConditionalSurvivalForestModel对象,设置树的数量为200
model = ConditionalSurvivalForestModel(num_trees=200)
# 使用训练数据拟合模型
model.fit(
X_train, # 特征数据
T_train, # 时间数据
E_train, # 事件数据
max_features="sqrt", # 每棵树使用的最大特征数量为sqrt(总特征数量)
max_depth=3, # 每棵树的最大深度为3
min_node_size=20, # 每个节点的最小样本数为20
alpha=0.05, # 用于计算置信区间的显著性水平为0.05
seed=42, # 随机种子为42
sample_size_pct=0.63, # 每棵树的样本数量为总样本数量的63%
num_threads=-1 # 使用所有可用的线程数进行并行计算
)
ConditionalSurvivalForestModel
# 导入所需的函数和模块
# 这里没有给出具体的导入语句,假设已经导入了所需的函数和模块
# 计算模型的一致性指数(concordance index)
ci = concordance_index(model, X_test, T_test, E_test)
print("concordance index: {:.2f}".format(ci))
# 输出模型的一致性指数,保留两位小数
# 计算模型的综合布里尔分数(integrated Brier score)
ibs = integrated_brier_score(model, X_test, T_test, E_test, t_max=12, figure_size=(15,5))
print("integrated Brier score: {:.2f}".format(ibs))
# 输出模型的综合布里尔分数,保留两位小数
concordance index: 0.93

integrated Brier score: 0.06
我们之前讨论了一下一致性得分,现在来谈一下布里尔得分:布里尔得分衡量了实际流失状态和估计概率之间的平均差异:观察到的生存状态(0或1)与给定时间t的生存概率之间的平均平方距离。它的取值范围在0到1之间,0是最优值:生存函数能够完美预测生存状态(布里尔得分)。
PySurvival的compare_to_actual方法绘制了高风险客户预测数量和实际数量随时间的变化。它还计算了三个准确性指标,即RMSE、MAE和中位数绝对误差。在内部,它使用Kaplan-Meier估计器来确定源数据的实际生存函数。
# 定义一个函数compare_to_actual,用于比较模型预测结果与实际结果的差异
# 调用compare_to_actual函数,传入参数,并将返回结果赋值给res变量
res = compare_to_actual(
model,
X_test,
T_test,
E_test,
is_at_risk=False,
figure_size=(16, 6),
metrics=["rmse", "mean", "median"]
)
# 打印"accuracy metrics:"字符串
print("accuracy metrics:")
# 使用列表推导式遍历res字典的键值对,并打印出来
_ = [print(k, ":", f'{v:.2f}') for k, v in res.items()]

accuracy metrics:
root_mean_squared_error : 0.88
median_absolute_error : 0.07
mean_absolute_error : 0.50
应用:CLV

并非所有的客户都具有相同的价值:来源
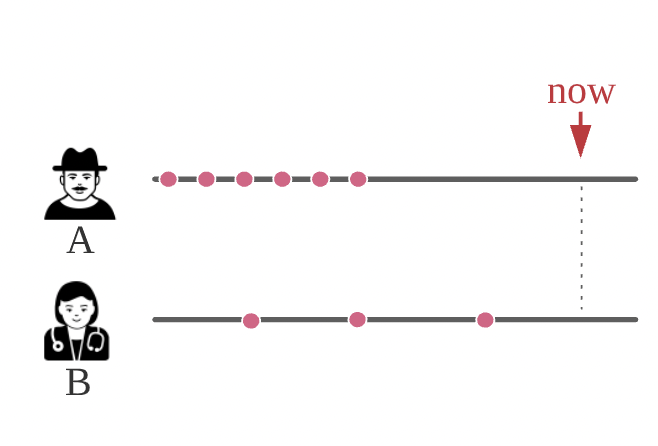
假设:
-
我们关注那些成功购买的客户
-
流失是永久性和潜在性的
结合客户的时间模式和他们购买价值的信息可以用不同的方式处理 - 我们将使用BG-NBD:Beta-Geometric Negative Binomial Distribution。有关详细描述,请阅读这篇优秀的Medium文章:https://towardsdatascience.com/customer-lifetime-value-estimation-via-probabilistic-modeling-d5111cb52dd;
原始论文也值得一读,链接在这里:http://brucehardie.com/papers/018/fader_et_al_mksc_05.pdf。
TL;DR版本:
-
一个周期内的CLV = 预测交易次数 x 预测每次购买的价值
-
BG-NBD关注交易的动态 - 每个客户的购买率不同
-
交易次数:泊松过程
-
间隔时间:指数分布
-
购买行为的变化:伽马分布
-
流失:几何分布
-
流失的变化:贝塔分布
-
数据的RFM格式:Recency(最近一次购买时间),Frequency(购买频率),Monetary value(购买金额)
我们将使用Elo Merchant Category Recommendation竞赛的数据来演示这种方法。
# 导入pandas库
import pandas as pd
# 读取csv文件,文件路径为'../input/elo-merchant-category-recommendation/historical_transactions.csv'
# 读取前500000行数据
# 仅保留'card_id','purchase_date','purchase_amount'这三列数据
df1 = pd.read_csv('../input/elo-merchant-category-recommendation/historical_transactions.csv',
nrows=500000,
usecols=['card_id', 'purchase_date', 'purchase_amount'])
# 将'purchase_date'列的数据转换为日期格式
df1['purchase_date'] = pd.to_datetime(df1['purchase_date'])
# 显示前5行数据
df1.head(5)
| card_id | purchase_amount | purchase_date | |
|---|---|---|---|
| 0 | C_ID_4e6213e9bc | -0.703331 | 2017-06-25 15:33:07 |
| 1 | C_ID_4e6213e9bc | -0.733128 | 2017-07-15 12:10:45 |
| 2 | C_ID_4e6213e9bc | -0.720386 | 2017-08-09 22:04:29 |
| 3 | C_ID_4e6213e9bc | -0.735352 | 2017-09-02 10:06:26 |
| 4 | C_ID_4e6213e9bc | -0.722865 | 2017-03-10 01:14:19 |
# 对数据框 df1 中的 purchase_date 列进行描述性统计分析
df1.purchase_date.describe() # 使用describe()函数对purchase_date列进行统计分析,返回该列的统计信息
count 500000
unique 480174
top 2017-11-24 00:00:00
freq 441
first 2017-01-01 00:46:31
last 2018-02-28 23:43:23
Name: purchase_date, dtype: object
# 导入所需的函数
from lifetimes.utils import summary_data_from_transaction_data
# 将交易数据转换为RFM格式
# 参数说明:
# transactions:交易数据,即原始数据框
# customer_id_col:顾客ID所在的列名
# datetime_col:交易日期所在的列名
# monetary_value_col:交易金额所在的列名
# freq:时间间隔的单位,这里设置为天('D')
rfm = summary_data_from_transaction_data(transactions=df1,
customer_id_col='card_id',
datetime_col='purchase_date',
monetary_value_col='purchase_amount',
freq='D')
# 显示转换后的RFM数据的前3行
rfm.head(3)
| frequency | recency | T | monetary_value | |
|---|---|---|---|---|
| card_id | ||||
| C_ID_002198cdf1 | 51.0 | 176.0 | 195.0 | -1.189117 |
| C_ID_0032aebb26 | 150.0 | 241.0 | 242.0 | -1.659501 |
| C_ID_003839dd44 | 159.0 | 403.0 | 408.0 | -0.940783 |
A convenient tool in lifetimes is calibration-retention segmentation.
# 导入所需的函数
from lifetimes.utils import calibration_and_holdout_data
# 使用calibration_and_holdout_data函数生成RFM模型所需的数据集
# 参数transactions为交易数据集,customer_id_col为顾客ID列名,datetime_col为交易日期列名,monetary_value_col为交易金额列名
# freq为时间单位,calibration_period_end为校准期结束日期,observation_period_end为观察期结束日期
rfm_cal_holdout = calibration_and_holdout_data(transactions=df1,
customer_id_col='card_id',
datetime_col='purchase_date',
monetary_value_col='purchase_amount',
freq='D',
calibration_period_end='2017-12-31',
observation_period_end='2018-02-28')
# 输出数据集的前3行
rfm_cal_holdout.head(3)
| frequency_cal | recency_cal | T_cal | monetary_value_cal | frequency_holdout | monetary_value_holdout | duration_holdout | |
|---|---|---|---|---|---|---|---|
| card_id | |||||||
| C_ID_002198cdf1 | 32.0 | 135.0 | 136.0 | -1.165039 | 19.0 | -0.648992 | 59.0 |
| C_ID_0032aebb26 | 111.0 | 173.0 | 183.0 | -1.571031 | 39.0 | -0.716737 | 59.0 |
| C_ID_003839dd44 | 135.0 | 348.0 | 349.0 | -0.912989 | 24.0 | -0.692921 | 59.0 |
# 导入BetaGeoFitter模型
from lifetimes import BetaGeoFitter
# 创建BetaGeoFitter模型对象,设置惩罚系数为0.9
bgf = BetaGeoFitter(penalizer_coef=0.9)
# 使用fit()方法拟合模型,传入参数为:
# frequency:每个客户在观察期内购买的次数
# recency:每个客户最近一次购买距离观察期结束的时间
# T:每个客户在观察期内的总时间
bgf.fit(frequency=rfm_cal_holdout['frequency_cal'],
recency=rfm_cal_holdout['recency_cal'],
T=rfm_cal_holdout['T_cal'])
<lifetimes.BetaGeoFitter: fitted with 2399 subjects, a: 0.01, alpha: 1.54, b: 0.19, r: 0.53>
评估诊断?很容易。
# 导入plot_period_transactions函数
# 该函数用于绘制BG/NBD模型的交易周期图
# 调用plot_period_transactions函数,并将结果赋值给变量_
# bgf是BG/NBD模型的实例
# 绘制交易周期图,显示BG/NBD模型的交易周期情况
from lifetimes.plotting import plot_period_transactions
# 调用plot_period_transactions函数,绘制BG/NBD模型的交易周期图,并将结果赋值给变量_
_ = plot_period_transactions(bgf)

预测结果:
# 选择第13个样本客户进行分析
# 首先,我们需要检查该客户在校准期和观察期的购买频率、最近一次购买时间和购买总金额
sample_customer = rfm_cal_holdout.iloc[13]
frequency_cal 68.000000
recency_cal 280.000000
T_cal 296.000000
monetary_value_cal -1.571509
frequency_holdout 5.000000
monetary_value_holdout -0.729487
duration_holdout 59.000000
Name: C_ID_01b098ff01, dtype: float64
# 使用贝叶斯Gamma分布模型(BG/NBD)对样本客户的未来交易次数进行预测
# 预测的时间窗口为60天
# 频率参数使用样本客户的计算频率
# 回购间隔参数使用样本客户的计算回购间隔
# T参数使用样本客户的计算T值
n_transactions_pred = bgf.predict(t=60, frequency=sample_customer['frequency_cal'], recency=sample_customer['recency_cal'], T=sample_customer['T_cal'])
# 预测未来交易次数,并将结果赋值给n_transactions_pred变量
13.68081350614679
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- Uncaught ReferenceError: videojs is not defined
- Nginx负载均衡以及常用的7层协议和4层协议的介绍
- 【Java数据结构 -- 队列:队列有关面试oj算法题】
- 在浏览器输入一个url,浏览器会发生什么?
- react+antd,Table表头文字颜色设置
- 循环练习题
- .gitignore和git lfs学习
- Zoho SalesIQ:提高品牌在社交媒体上参与度的实用指南
- 【Leetcode】计算器
- 从传统到智能:机器视觉检测赋能PCB行业数字化转型!