代码随想录算法训练营第27天 | 39.组合总和 40.组合总和II 131.分割回文串

组合总和

注意这道题组合中元素数目不定，同时数组中的元素可以使用无限多次。
虽然数目不定，但还是题中仍然给出了总和的限制，我们可以用总和作为递归终止条件。数组中的元素可以使用无数次，这与之前的题目不同，决定了这道题 startIndex 不同于之前的题目。
关于 startIndex：当从一个集合中取元素进行组合时，为了去重的需要，是要有 startIndex 的；如果每一次取元素来自不同集合，而且多个集合彼此相互独立，就不需要有，比如电话那道题。

class Solution{
public:
	vector<vector<int>> result;
	vector<int> path;
	void backtracking(vector<int>& candidates, int target, int startIndex){
		if(target == 0){
			result.push_back(path);
			return;
		}
		for(int i = startIndex; i < candidates.size() && target - candidates[i] >= 0; i++){
			path.push_back(candidates[i]);
			backtracking(candidates, target - candidates[i], i);
			path.pop_back();
		}
	}
	vector<vector<int>> combinationSum(vector<int>& candidates, int target){
		result.clear();
		path.clear();
		sort(candidates.begin(), candidates.end());
		backtracking(candidates, target, 0);
		return result;
	}
};

对于这里对总和进行剪枝，要注意先排序。

组合总和II

这道题不同于上一道题的特点是数组内的每一个元素都只能使用一次，同时数组内是含有相同元素的。最终仍然不能输出重复的组合，那么这里的去重就十分关键了。
关于去重：我们将整个递归回溯抽象为树结构。我们使用 startIndex 实际上保证了在同一树枝上不会重复的元素（这里的重复不是说元素值重复，而是说重复地取了同一个元素）。但为了保证最终的输出不包含重复的集合，我们还需要在每一步（树层）做选择时不要选择值重复访元素。这才是这道题关键的去重。
排序也是解决“树层”去重问题的好方法。

class Solution{
public:
	vector<vector<int>> result;
	vector<int> path;
	void backtracking(vector<int>& candidates, int target, int startIndex){
		if(target == 0){
			result.push_back(path);
			return;
		}
		for(int i = startIndex; i < candidates.size() && target - candidates[i] >= 0; i++){
			// 排序后相同的元素都是连着的，所以可以直接判断当前元素是否与上一个相同来进行树层去重
			if(i > startIndex && candidates[i] == candidates[i - 1]){
				continue;
			}
			path.push_back(candidates[i]);
			backtracking(candidates, target - candidates[i], i + 1);  // 因为每个元素只能使用一次，startIndex要加1
			path.pop_back();
		}
	}
	vector<vector<int>> combinationSum2(vector<int>& candidates, int target){
		result.clear();
		path.clear();
		sort(candidates.begin(), candidates.end());
		backtracking(candidates, target, 0);
		return result;
	}
};

分割回文串

如何模拟分割过程呢？将分割类比为我们上面熟悉的组合问题，先切第一个字母，判断回文串回溯，继续切后面的字符。可以将切割过程抽象为下面的树结构。

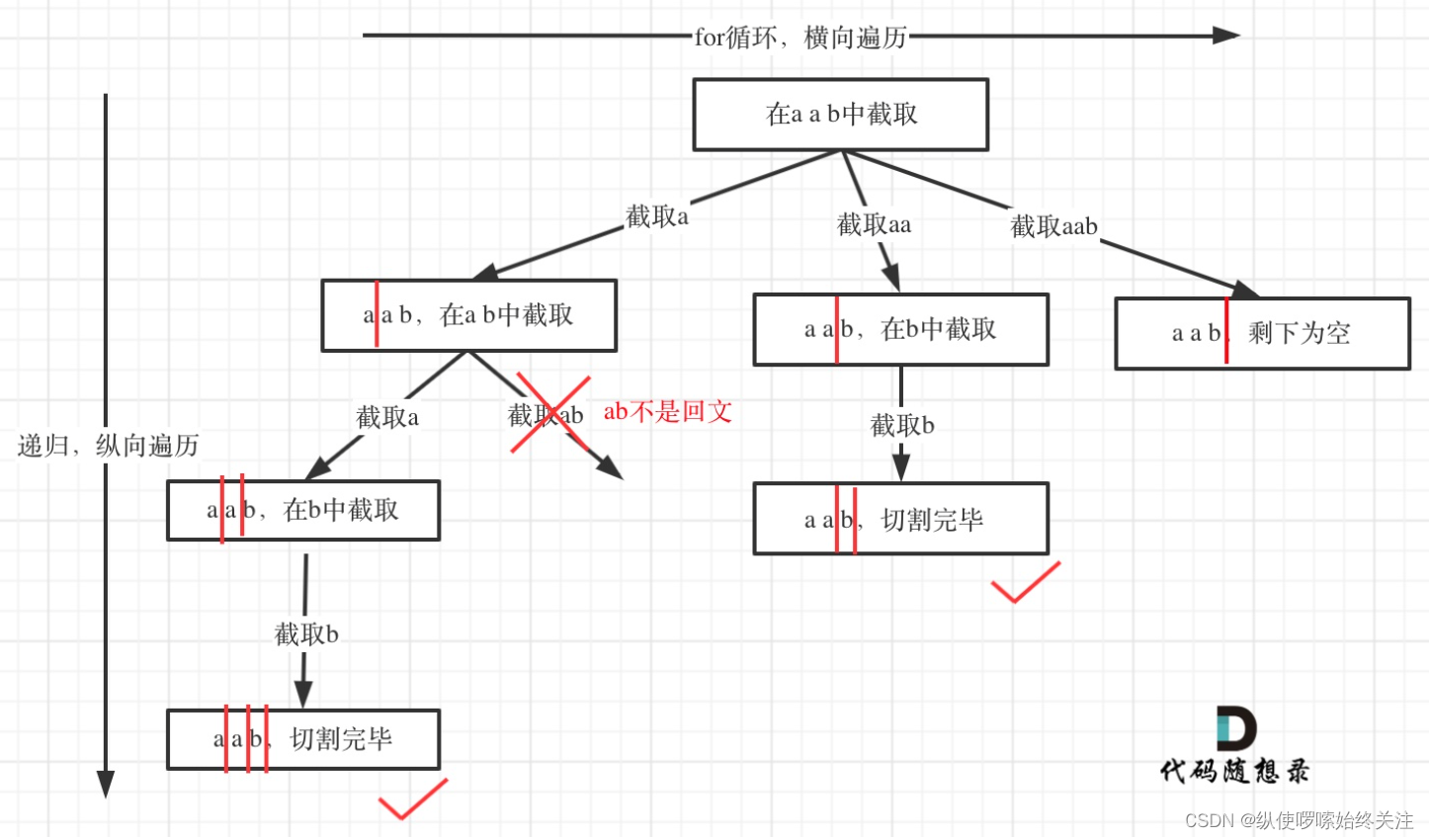
这样就不难写出代码了，在单层递归逻辑中从 startIndex 开始进行 for 循环，模拟截取不同长度的字符。在进入下一层循环时要将下标 i + 1，从剩余的字符串中开始切割。当 startIndex等于字符串长度时，说明已经找到了一个符合条件的切割方法，这里也需要判断不是回文串时的处理方法配合。

class Solution{
public:
	vector<vector<string>> result;
	vector<string> path;
	bool isPalindrome(string s, int start, int end){  // 双指针方法
		for(int i = start, j = end; i < j; i++, j--){
			if(s[i] != s[j])  return false;
		}
		return true;
	}
	void backtracking(string s, int startIndex){
		if(startIndex == s.size()){
			result.push_back(path);
			return;
		}
		for(int i = startIndex; i < s.size(); i++){
			if(isPalindrome(s, startIndex, i)){  // 判断是否回文串
				string str = s.substr(startIndex, i - startIndex + 1);  // 切割出子串
				path.push_back(str);
			}
			else  continue;  // 不是回文串，那就不继续回溯，丢掉这种切割
			backtracking(s, i + 1);  // 下一层递归从未被切割的字符开始，因此i + 1
			path.pop_back();
		}
	}
	vector<vector<string>> partition(string s){
		result.clear();
		path.clear();
		backtracking(s, 0);
		return result;
	}
};

这里对回文串的判断时间复杂度是比较大的，每次都需要遍历判断，其实这里可以通过动态规划来优化，因为这里有一个递推关系就是 s[i:j] 是否是回文串取决于 s[i+1:j-1] 与 s[i] == s[j]。

class Solution{
public:
	vector<vector<string>> result;
	vector<string> path;
	vector<vector<bool>> isPalindrome;
	void computePalindrome(string s){
		isPalindrome.resize(s.size(), vector<bool>(s.size(), false));
		for(int i = s.size() - 1; i >= 0; i--){  // 这里的遍历顺序是由s[i][j]取决于s[i+1][j-1]决定的
			for(int j = i; j < s.size(); j++){
				if(i == j)  isPalindrome[i][j] = true;
				else if(j == i + 1 && s[i] == s[j])  isPalindrome[i][j] = true;
				else  isPalindrome[i][j] = isPalindrome[i + 1][j - 1] && (s[i] == s[j]);
			}
		}
	}
	void backtracking(string s, int startIndex){
		if(startIndex == s.size()){
			result.push_back(path);
			return;
		}
		for(int i = startIndex; i < s.size(); i++){
			if(isPalindrome[startIndex][i]){
				string str = s.substr(startIndex, i - startIndex + 1);
				path.push_back(str);
			}
			else  continue;
			backtracking(s, i + 1);
			path.pop_back();
		}
	}
	vector<vector<string>> partition(string s){
		result.clear();
		path.clear();
		computePalindrome(s);
		backtracking(s, 0);
		return result;
	}
};