二进制、位运算和掩码运算，小白鼠测试示例

1. 二进制

二进制是一种基于两个数字0和1的数制系统。它可以表示两种状态，即开和关。所有输入电脑的任何信息最终都要转化为二进制。目前通用的是ASCII码。最基本的单位为bit。
在计算机科学中，二进制是最常用的数制系统，因为计算机内部的所有数据都是以二进制形式存储和处理的。

在二进制中，每个数字位被称为一个比特（bit），它可以是0或1。比特的位置从右到左依次递增，每个位置的值是2的幂。比如，最右边的比特的权重是2^{0，即1；第二个比特的权重是2}1，即2；第三个比特的权重是2^2，即4，依此类推。

使用二进制，可以表示和处理各种数据，包括整数、小数、字符和图像等。例如，整数10可以表示为二进制的1010，其中的1代表相应的位为1，0代表相应的位为0。

二进制还可以进行各种运算，包括加法、减法、乘法和除法等。这些运算和十进制的运算类似，只是使用的数码是0和1而已。

2. 位运算

二进制位运算是对二进制数进行逐位的逻辑运算，包括位与（&）、位或（|）、位异或（^）、位取反（~）等操作。

2.1 二进制位运算符及其示例

1. 与运算（&）：两个相应位上的数字都为1时，结果为1，否则为0。
   示例：

   1101 & 1011 = 1001

2. 或运算（|）：两个相应位上的数字中只要有一个为1时，结果为1，否则为0。
   示例：

1101 | 1011 = 1111

3. 异或运算（^）：两个相应位上的数字不同则结果为1，相同则结果为0。
   示例：

1101 ^ 1011 = 0110

4. 非运算（~）：对一个二进制数的每个位取反。
   示例：

~1101 = 0010

5. 左移运算（<<）：将一个二进制数的所有位向左移动指定的位数。
   示例：

1101 << 2 = 10100

6. 右移运算（>>）：将一个二进制数的所有位向右移动指定的位数。
   示例：

1101 >> 2 = 0011

3. 二进制示例之试毒小白鼠

二进制很强大，在某些方面有着很显著的作用，以下是一个关于二进制的小栗子：

• 老鼠试毒

问题：
有100瓶水，其中有一瓶有毒，小白鼠只要尝到带毒的水24小时后就会死亡，问至少要多少只小白鼠才能在24小时后鉴别出哪瓶水有毒？
答：
按道理来说，应该是100只，肯定是能鉴别出来的。但问题是至少要多少只可以鉴别出，求最少，所以肯定不能直接填写100.

这里借助二进制运算就可以巧妙的解决此问题。

这样，先将问题简化一下：假设只有8瓶水，其中1瓶有毒，如下：

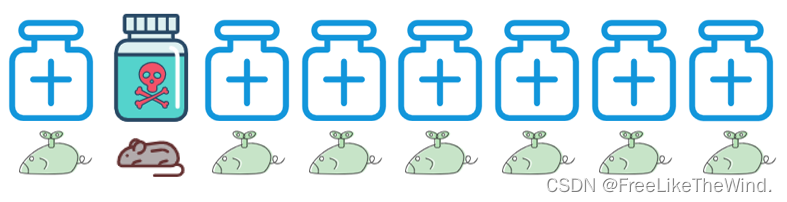
设给水编个号(根据二进制计算)：

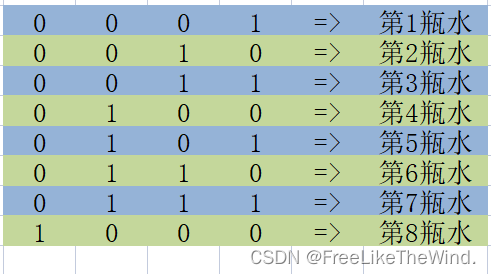
经过矩阵转置，变为：

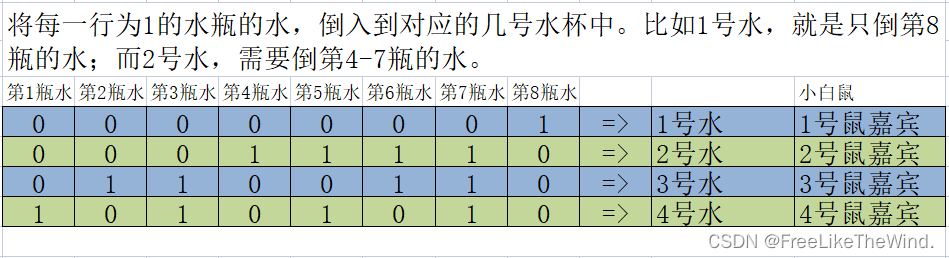
找来四只小白鼠，按照水号的顺序，分别给小白鼠命名为1号鼠嘉宾、2号鼠嘉宾、3号鼠嘉宾、4号鼠嘉宾。
依次喝对应水号的水，观察24小时，根据状态（死亡为1，活着为0）查找上图中的对应的数字，然后将二进制转换成十进制，可以得出哪瓶水是有毒的。

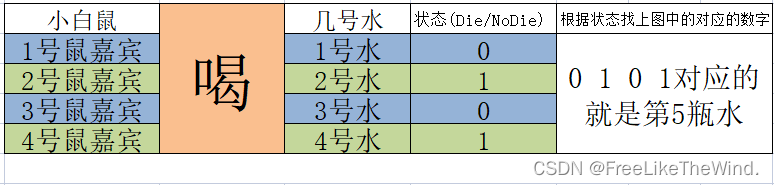
因此，当有8瓶水，其中一瓶有毒时，仅仅只需要4只小白鼠就可以测出哪瓶是有毒的。
将话题扩大到100瓶水。
2的6次方是64,2的7次方是128.因此按照上面的算法，可以得出，需要7只小白鼠。
设（每瓶水一个不同的编号）：

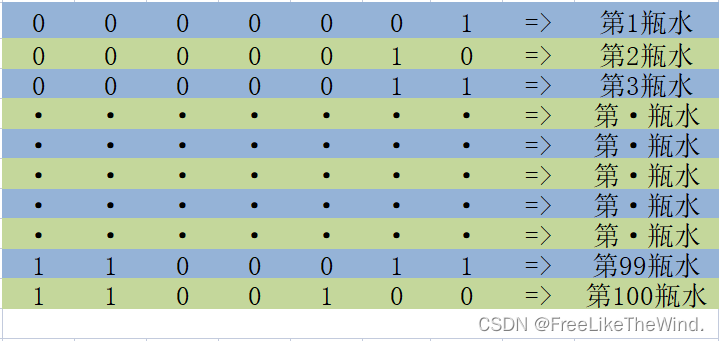
矩阵转置：

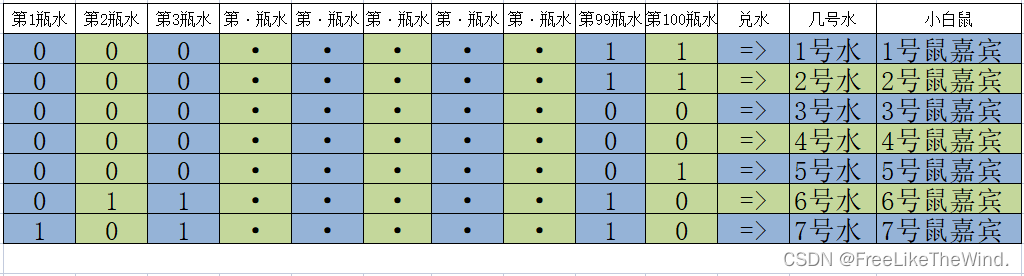
接下来就是小白鼠和对应的水，根据小白鼠的生存状态，可以得出哪瓶水有毒。

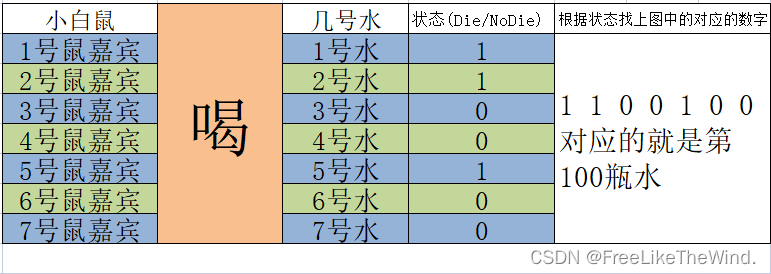
4. 掩码运算

掩码操作是指利用位运算符对特定位置的二进制位进行设置或清除。

1. 设置某一位置为1：使用位或运算符（|）将要设置的位和当前值进行位或操作。
   例如，将第3位设置为1：

int value = 4;  // 二进制表示为00000100
value = value | (1 << 2);  // 将第3位设置为1，结果为00000100 | 00000100 = 00000100

2. 清除某一位置为0：使用位与运算符（&）将要清除的位取反后和当前值进行位与操作。
   例如，将第5位清除为0：

int value = 22;  // 二进制表示为00010110
value = value & ~(1 << 4);  // 将第5位清除为0，结果为00010110 & 11101111 = 00000110

3. 切换某一位置的值：使用位异或运算符（^）将要切换的位和当前值进行位异或操作。
   例如，切换第2位的值：

int value = 10;  // 二进制表示为00001010
value = value ^ (1 << 1);  // 切换第2位的值，结果为00001010 ^ 00000010 = 00001000

4. 检查某一位是否为1：使用位与运算符（&）将要检查的位和当前值进行位与操作，判断结果是否为0。
   例如，检查第7位是否为1：

int value = 127;  // 二进制表示为01111111
int mask = 1 << 6;  // 设置掩码为第7位的1，即01000000
int result = value & mask;  // 结果为01111111 & 01000000 = 01000000
if(result != 0) {
    // 第7位为1
} else {
    // 第7位为0
}

5. 取某几位掩码

有两种方式取第几位到第几位的掩码：

• 方法一：

// 比如取第3位到第7位的掩码，就是设置第3位到第7位为1
// 掩码： 11111000
// 往左偏移7+1位 - 往左偏移3位 = 7-3位都是1
int mask = (1 << 8) - (1 << 3);

为了验证结果是否是正确的，直接输出"11111000"的转换为10进制的值：

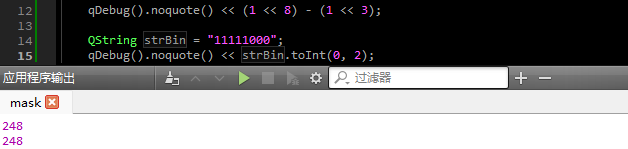
• 方法二：
  使用bitset

	// 需引入头文件<bitset.h>
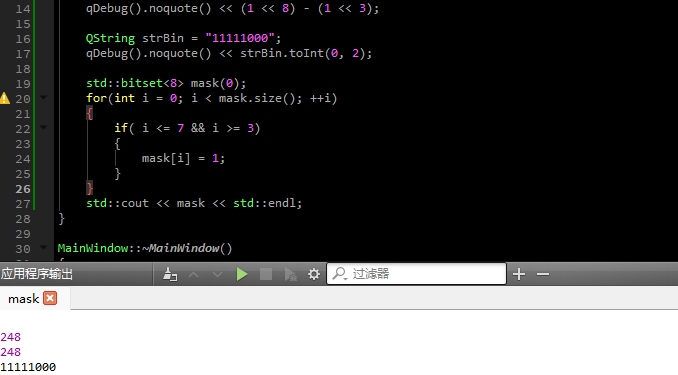
    std::bitset<8> mask(0);
    for(int i = 0; i < mask.size(); ++i)
    {
        if( i <= 7 && i >= 3)
        {
            mask[i] = 1;
        }
    }
    std::cout << mask << std::endl;

结果如下：

6. 结论

位运算符可以用于执行各种操作，例如掩码操作、位清零、位设置、位翻转等。
在实际编程中，位运算常用于位操作、优化算法和处理二进制数据等场景，能够提高效率和灵活性。

明天就要见对方家长了，好忐忑啊，毕竟是我先打的他们家小孩。