FAST-LIO论文解析

题目：FAST-LIO：一种快速鲁棒的基于紧耦合迭代卡尔曼滤波的雷达-惯导里程计

摘要

本文提出了一种计算效率高、鲁棒性好的激光-惯性里程计框架。我们使用紧耦合的迭代扩展卡尔曼滤波器将LiDAR特征点与IMU数据融合在一起，从而在快速运动、嘈杂或混乱的环境中实现鲁棒导航。为了在大量测量数据的情况下降低计算负荷，我们提出了一个新的计算卡尔曼增益的公式。新公式的计算量依赖于状态维数而不是测量维数。在各种室内和室外环境中对所提出的方法及其实现进行了测试。在所有测试中，我们的方法实时产生可靠的导航结果:在四旋翼机载计算机上运行，它在扫描中融合了1200多个有效特征点，并在25毫秒内完成了iEKF步骤的所有迭代。我们的代码在Github2开源。

一、简介

主要贡献：

---

1. 紧耦合卡尔曼滤波器，使用IMU运动模型的积分结果和点云匹配残差共同构建残差函数
2. 里程计频率，以固定采样时间间隔作为一个SCAN进行处理，而不是将整个激光帧作为一个处理单位
   如一帧点云采样时间为100ms，将20ms作为一个SCAN，即将一帧激光点云变成5个SCAN
3. 点云运动补偿，基于IMU积分结果反推每个激光点采样时间对应的位姿，将所有的激光点变换到SCAN结束时间对应的坐标系
4. 卡尔曼增益计算，优化计算公式，将针对激光点的矩阵求逆转换为对状态的矩阵求逆，维度几大降低

---

二、相关工作

A.纯LIDAR方法

基于ICP、G-ICP进行匹配，以及结合点到平面和点到直线的距离进行迭代匹配计算(LOAM、Lego-Loam)。

B.松耦合LIO

将IMU的积分结果作为点云匹配的初值，或者对IMU积分以及点云匹配分别处理，然后再基于EKF进行滤波融合。

C.紧耦合LIO

将原始云点数据和IMU原始数据一起放在图优化或者滤波器中构建残差函数，并进行优化。

三、算法概述

A. 算法框架

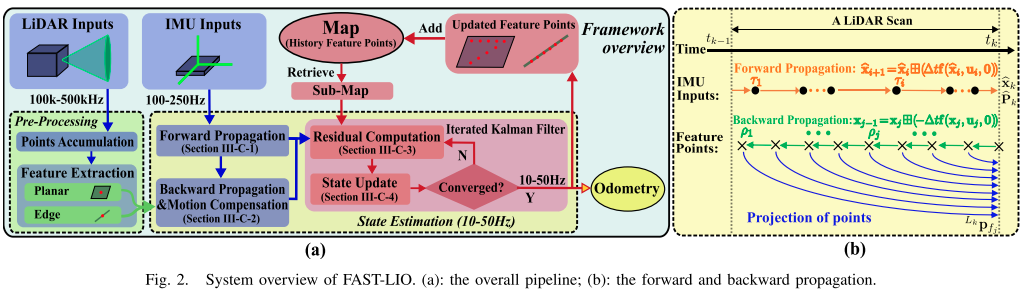
本文将使用表1中所示的符号。我们的工作流程概述如图2所示。将激光雷达输入输入特征提取模块，获得平面特征和边缘特征。然后将提取的特征和IMU测量值输入我们的状态估计模块，在10Hz?50Hz下进行状态估计。然后，估计的姿态将特征点变换到世界坐标系并添加到全局地图。

---

• $t_k$ : 某组scan数据的终止时间
• ${\tau }_i$ : 在两帧LIDAR时间戳区间内，第i个IMU数据对应时间
• ${\rho }_j$ : lidar帧中第j个云点对应时间
• $I_i$、$I_j$、$I_k$ ： 在$t_k$、${\tau }_i$、${\rho }_j$时对应的IMU坐标系
• $L_i$、$L_k$ : ${\rho }_j$、$t_k$时对应的LIDAR坐标系
• $x,\hat{x},\bar{x}$ : 状态估计时的真值、预测值和估计值
• $\tilde{x}$ : 真值和估计值之间的差值
• ${\hat{x}}^k$ : 第k次迭代时的预测值
• $x_i$、$x_j$、$x_k$ : i,j,k时刻的状态向量
• ${\stackrel{?}{x}}_j$ :在j时刻的后向传播位姿

---

B. 系统描述

1.运算符介绍

略。

2.LIDAR数据预处理

每帧激光雷达点的坐标系都是当前时刻对应的运动坐标系，由于原始激光雷达点的采样频率非常高(如200HZ，这里指的是激光雷达在扫描时采样频率，不是单帧激光雷达数据的频率)，因此不可能在接受到每个新点后进行处理，更实际的方法是在一定时间内积累这些点，并一次处理他们(参考IMU预积分)。在Fast-Lio中，最小累计间隔为20ms，实现50HZ的位姿输出和地图更新，如图2(a)所示。这样的累计点集成为scan，一次处理时间为$t_k$(见图2 b)。从原始点中提取局部平滑度较高的平面点和局部平滑度低的边缘点。

平面点和边缘点的提取使用LOAM中的方法，此外在边缘特征提取时加入了对强度信息的考虑，即强度平滑度大的点同样被提取为线特征。

假设特征点的数量为m，采样时间间隔为$\left(t_{k?1},t_k\right]$，且${\rho }_m=t_k$。
定义特征点为：

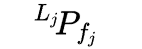
其中$L_j$为${\rho }_j$时刻的LIDAR坐标系。对于一次激光数据的扫描，同样存在一组IMU测量数据，采样时间间隔为$\left[t_{k?1},t_k\right]$,IMU数据的起止时间不一定与scan起止时间相同。

C.状态估计

为了估计状态公式(2)中的状态，我们使用迭代扩展卡尔曼滤波器。此外，我们在状态估计的切空间中描述估计协方差。

假设$t_{k?1}$时刻最后一次LiDAR扫描的最优状态估计为${\bar{x}}_{k?1}$，协方差矩阵为${\bar{P}}_{k?1}$。则${\bar{P}}_{k?1}$表示随机误差状态向量的协方差定义如下:

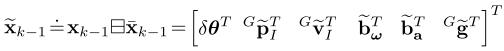
该公式表示状态估计误差 = 真实值 - 估计值

其中旋转误差为旋转矩阵乘的性质，其余为向量减的性质。

另外，FAST-LIO是基于IEKF实现的状态估计，所以需要了解一些EKF中的概念：

---

• 预测值：指通过过程模型(如积分为代表的运动模型)，基于上一时刻的最优值和运动模型预测的理想结果，预测值需要加上噪声影响才更接近真值
• 观测值：指直接通过传感器获得测量数据，如IMU的线加速度和角速度
• 估计值：指在EKF的更新步骤中，结合预测值和估计值得到的最接近真值的最优解

---

1.前向传播

即基于IMU数据，通过运动模型对角速度和线加速度进行积分，根据上一时刻的估计值和当前时刻的运动求解得到的理想预测值，同时计算误差的协方差矩阵

（1）状态预测
公式4是指过程模型，即对于第k组数据的不断积分的过程第i+1次迭代的预测值 = 第i次迭代的预测值 + 一次积分结果，i=1时第0次迭代的预测值即k-1时刻的估计值

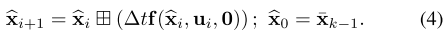
公式5是指误差模型，即对于第k组数据的每一次迭代，第i+1时刻的状态误差 = 第i+1时刻的考虑噪声影响的估计值 - 第i+1时刻的不考虑噪声影响理想预测值

第i+1时刻的考虑噪声影响的估计值即公式2，由第i时刻的真值加上i到i+1时刻考虑噪声影响的积分结果得到

第i+1时刻的不考虑噪声影响理想预测值即公式4,由i时刻的理想预测值加上不含噪声的积分结果得到

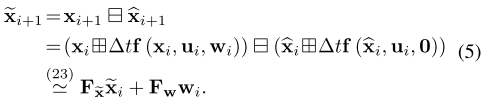
（2）计算误差的协方差矩阵

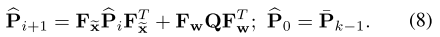
2.反向传播和运动补偿

即通过运动补偿进行激光点云去畸变。

当点云累计时间间隔达到$t_k$时，就会进入下一个scan，该scan的位姿估计需要在上一个scan的位姿x和误差协方差矩阵基础上进行更新。虽然在时间上是连续的，但是新的scan坐标系已经改变了。

为了补偿新scan中某个点${\rho }_j$到上一scan坐标系之间的运动畸变，对公式（2）进行反向传播得到以下公式：

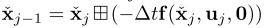
这里需要参考图2-b进行理解，在前向传播过程中基于IMU数据我们得到了$t_{k?1}$到$t_k$的运动，以及$t_k$时刻的估计值，现在为了对雷达点进行运动补偿，根据反向传播公式由$t_k$时刻位姿得到${\rho }_j$时刻的位姿，然后得到${\rho }_{j?1}$时刻位姿，以此类推，通过j=i到j=t_k每个时刻的位姿，可以将对应的云点坐标系全部转换到$t_k$时刻坐标系。

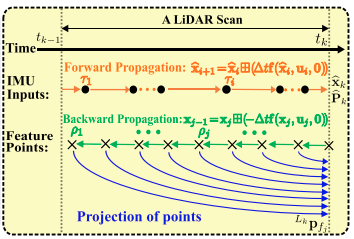
反向传播会根据特征点的频率执行，特征点的频率通常比IMU频率高的多(注意，这里描述的不是点云频率，而是点的频率，常见的机械式激光雷达、固态激光雷达点云频率通常为5、10、15、20HZ，而点的频率是非常高的，例如16线的velodyne，点云频率为10HZ，每条激光线束通常有2000个点，16x2000/0.1即为点的频率)。

对于两帧IMU测量之间采样的所有特征点，我们使用左IMU测量作为反向传播的输入。此外，注意到f(xj, uj, 0)的最后三个元素(对应于陀螺仪bias, 加速度计bias，与外参)为零(见公式3)，反向传播可简化为以下公式，即只针对位移、速度和旋转进行反向传播。

通过后向传播可以得到${\rho }_j$到scan结束时间$t_k$之间的相对运动，即旋转和平移变换。这一相对变换将每个点的坐标系都转换到scan结束时间$t_k$下的坐标系。

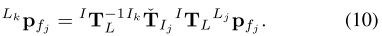
3.残差计算

经过运动补偿，可以将每个scan中的特征点都视为$t_k$时刻采集的点，并使用这组点构造残差。假定当前为$[t_{k?1},t_k]$下卡尔曼滤波器的第k次迭代，记此刻的状态估计为${\hat{X}}_k^k$。对于第0次迭代，${\hat{X}}_k^k={\hat{X}}_k$，即通过前向传播得到的初始状态估计。然后，该scan中的特征点可以通过公式11被转换到全局坐标系下：

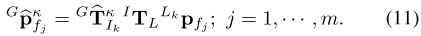
对于公式11,是先将k时刻的第j个特征点变换到k时刻的IMU坐标系下，然后再变换到全局坐标系下。对于每个LiDAR特征点，假设其附近特征点在地图中定义的最近的平面或边缘是该点真正所属的位置。也就是说，激光部分的残差被定义为坐标变换后的激光点到全局地图中对应边缘或平面的距离。定义$u_j$为特征点对应平面的法向量或者线段方向，则激光匹配的在第k次迭代的残差可以被定义为公式12：

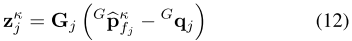
上述公式的物理含义为：残差 = 特征点的估计全局坐标 与 地图上最近的平面或边缘点 的距离。其中，特征点的估计全局坐标需要单独计算，而地图上最近的平面或边缘点则由kd-Tree中搜索得到。此外，我们只会考虑其标准值低于一定阈值(如 0.5m)的残差。而残差高于阈值的点会被定义为离群值或 新观测到的点。

4.迭代状态更新

为了融合激光点云匹配残差和上述IMU前向传播得到的当前状态估计${\bar{x}}_k$和误差协方差矩阵${\bar{P}}_k$，我们需要将残差$z_j^k$和真实状态$x_k$以及LIDAR的测量噪声相关联。LIDAR的测量噪声由测距噪声和激光束定向误差，通过公式13去除。

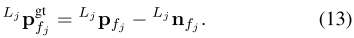
结合公式10、11、12、13可以得到以下残差方程

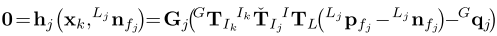
对于第k次迭代，将上述残差方程在${\bar{x}}_k$进行一阶泰勒展开，得到公式14：

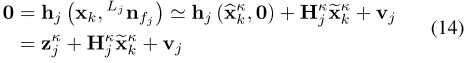
其中，$z_j^k$为点云匹配误差，H为残差函数的一阶雅格比，${\tilde{X}}_k^k$为状态估计的真实值与估计值之差，v表示LIDAR点的测量噪声。

$x_k$的先验分布是从第III-C.1节中的前向传播中获得，用于以下公式的计算：

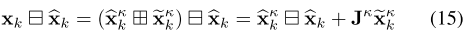
其中$J^k$为公式15在0处一阶泰勒展开的雅格比矩阵。

结合公式15的先验和公式14的后验分布，可以得到最大后验估计。公式15表示前向传播过程中IMU积分的先验误差，公式14表示点云匹配对应的残差。

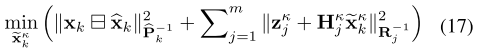
将公式15带入到个公式17,并且将二次项进行整理，可以得到公式18,卡尔曼滤波中更新过程中的卡尔曼增益和第k+1次迭代的估计值，如果第k+1次迭代时对应的残差小于一定阈值，则本次迭代结果为最优状态估计和协方差，即公式19。

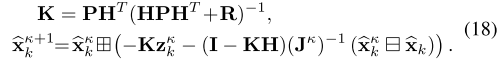
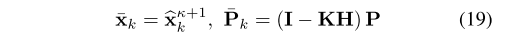
但由于激光雷达中的点数量庞大，在公式18求解卡尔曼增益时会对一个维度很大的矩阵求逆，在本文中将对激光数据的求解转移到对状态的求解，使维度极大得降低，得到新的卡尔曼增益形式。简单的来说就是将公式18中对$(HP{H}^T+R)$求逆，转变为对$(H^{T}R)$求逆

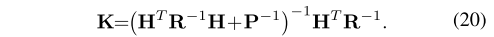
我们在附录B中基于矩阵逆引理证明了这两种形式的卡尔曼增益确实是等价的。由于激光雷达测量值是独立的，协方差矩阵R为对角矩阵，因此新公式只需要在状态维度上反转两个矩阵，而不需要在测量值上反转。新公式大大节省了计算量，因为状态维数通常比LIO中的测量值要低得多(例如，在10hz扫描速率下，扫描中有1000多个有效特征点，而状态维数只有18)。

5.算法伪代码

---

输入：上一个SCAN的最优状态估计${\bar{x}}_{k?1}$和${\bar{p}}_{k?1}$
当前SCAN对应的IMU数据$(a_m,w_m)$
当前SCAN的激光特征点

1. 基于前向传播得到状态预测值和先验误差的协方差矩阵
2. 基于后向传播得到运动补偿后的3D激光点
3. 迭代前：迭代次数k=-1,${\hat{X}}_k^{k=0}={\hat{X}}_k$
4. 迭代
   | 1. 迭代次数k=k+1
   | 2. 计算IMU前向传播先验一阶雅格比$J^k$和先验误差的协方差矩阵
   | 3. 计算点云匹配残差$z_j^k$和残差的一阶泰勒展开雅矩阵$H_j^k$
   | 4. 更新状态估计和卡尔曼增益
   结束：当本次误差和上次误差之间的差值小于某个阈值
5. 更新状态估计值${\bar{x}}_k$和后验估计协方差矩阵${\bar{P}}_k$

输出：${\bar{x}}_k$和${\bar{P}}_k$

---

D.地图更新

通过将求解得到的状态转化为旋转矩阵和平移向量，然后将雷达坐标系下的点转换到全局坐标系下，最后添加到全局地图中。

E.初始化

为了获得系统状态的良好初始估计(例如，重力矢量Gg、偏置和噪声协方差)，以便加速状态估计器，需要初始化。在FAST-LIO中，初始化很简单:将LiDAR保持静止几秒钟(本文中所有实验均为2秒)，然后使用收集到的数据初始化IMU偏差和重力矢量。如果激光雷达支持非重复扫描(例如Livox AVIA)，保持静态也允许激光雷达捕获初始高分辨率地图，这对后续导航有益。

四、试验结果

A.计算复杂度实验

对卡尔曼增益计算方法用时进行了对比，结果如下

B.无人机实验

主要对计算回环处的漂移现象，室内环境下32m的轨迹，漂移为8cm

C.室内实验

室内场景、快速选转运动，对FAST-LIO建图效果和LOAM以及LOAM+IMU松耦合进行了定性对比，建图效果略好，和FAST-LIO慢速运动下的建图效果相比则无较大差异。

里程计位姿输出上频率远高于loam,因为在FAST-LIO中是按照激光点的采样频率进行的状态估计，而非激光帧的频率。

D.室外实验

（1）基于手持激光雷达
在室外条件下，手持激光雷达进行快速选转，140的轨迹漂移为7cm。
（2）基于LINS室外数据集
处理时间： FAST-LIO为7.3ms，LINS为34.5ms
特征点数： FAST-LIO为784，LINS为147