104、Behind the Scenes: Density Fields for Single View Reconstruction
简介
?提出预测隐密度场方法,该密度场将输入图像视锥中的每个位置映射到体积密度。通过直接从可用视图中采样颜色,而不是在密度场中存储颜色,与NeRFs相比,所提出的场景表示变得明显不那么复杂,并且神经网络可以在一次前向传递中预测它,从视频数据中进行自我监督训练预测网络。该公式允许体绘制执行深度预测和新视图合成。
实现流程
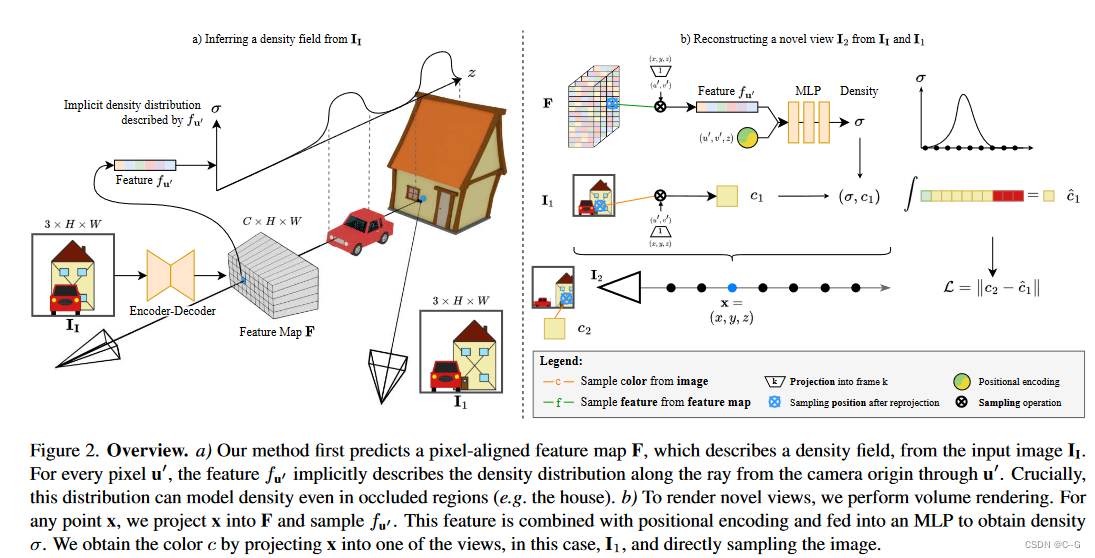
?输入图片 I I ∈ [ 0 , 1 ] 3 × H × W = ( R 3 ) Ω , Ω = { 1 , ? ? , H } × { 1 , ? ? , W } I_I \in [0,1]^{3 \times H \times W} = (\R^3)^\Omega,\Omega = \{ 1,\cdots,H \} \times \{ 1,\cdots,W \} II?∈[0,1]3×H×W=(R3)Ω,Ω={1,?,H}×{1,?,W},对应的世界-相机姿态矩阵和投影矩阵为 T I ∈ R 4 × 4 , K I ∈ R 3 × 4 T_I \in \R^{4 \times 4},K_I \in \R^{3 \times 4} TI?∈R4×4,KI?∈R3×4。在训练时一系列帧 I k , K ∈ N I_k,K\in N Ik?,K∈N 的集合为 N = { 1 , 2 , ? ? , n } N = \{1,2,\cdots,n\} N={1,2,?,n}。在假设齐次坐标的情况下,世界坐标中的一个点 x ∈ R 3 x\in\R^3 x∈R3 可以投影到坐标系 k 的像平面上, π K ( x ) = K K T K x \pi_K(x) = K_KT_Kx πK?(x)=KK?TK?x
Predicting a Density Field
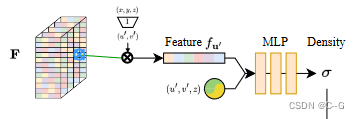
?从输入图像
I
I
I_I
II?中,编码器-解码器网络首先预测像素对齐的特征图
F
∈
(
R
C
)
Ω
F\in(\R^C)^Ω
F∈(RC)Ω,对特征
f
u
′
=
F
(
u
′
)
f_{u'} = F(u')
fu′?=F(u′) 进行双线性采样,结合位置编码
y
(
d
)
y(d)
y(d) 和像素位置编码
y
(
u
I
′
)
y(u'_I)
y(uI′?),通过MLP获得该点密度。
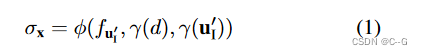
Volume Rendering with Color Sampling
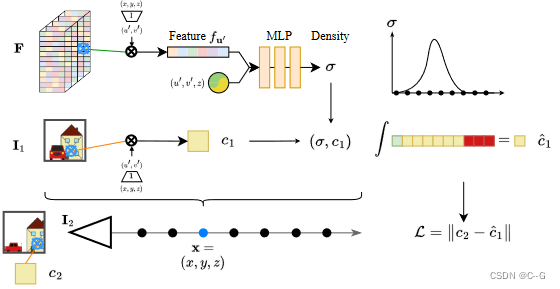
?将一个点 x 投影到一个坐标系 k 中,然后对颜色
c
x
,
k
=
I
K
(
π
K
(
x
)
)
c_{x,k} = I_K(\pi_K(x))
cx,k?=IK?(πK?(x)) 进行双线性采样,并结合体密度进行体渲染得到像素预测值。
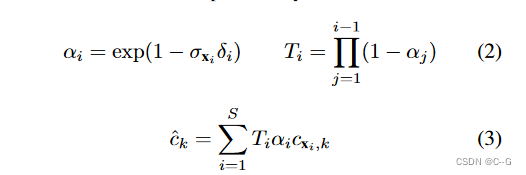
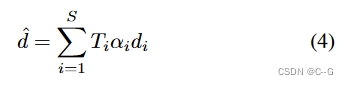
Behind the Scenes Loss Formulation
?首先从输入图像
I
I
I_I
II? 计算特征映射
F
F
F,得到所有帧集合
N
^
=
{
I
I
}
∪
N
\hat{N} = \{I_I\} \cup N
N^={II?}∪N,随机划分为两个集合
N
l
o
s
s
,
N
r
e
n
d
e
r
N_{loss},N_{render}
Nloss?,Nrender?,输入图像可以出现在这两个集合中的任何一个。使用相机姿态和预测密度从
N
r
e
n
d
e
r
N_{render}
Nrender? 中采样颜色,重建
N
l
o
s
s
N_{loss}
Nloss? 中的帧,重建图像帧与
N
l
o
s
s
N_{loss}
Nloss? 图像帧之间的光度一致性作为密度场的监督,随机采样p块
P
i
P_i
Pi? 来使用逐块光度测量,具体参考[Digging into self-supervised monocular depth estimation]。因此会产生2D损失为:
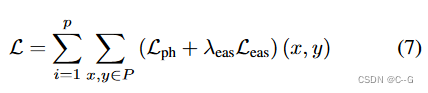
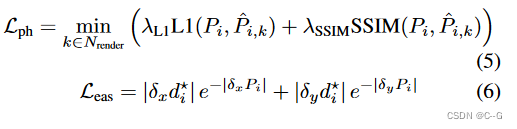
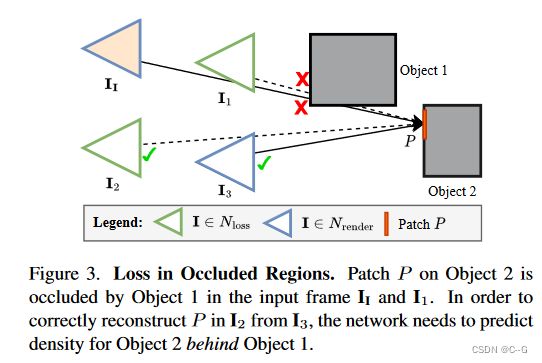
?训练期间,目标是在
I
k
I_k
Ik? 中重建区域 p 。基于
I
k
+
1
I_{k+1}
Ik+1? 采样颜色的重建将给出一个清晰的训练信号,即使该区域在
I
I
I_I
II? 中被遮挡,也能正确预测该区域的几何结构,为了学习有关被遮挡区域的几何形状,需要在训练期间除了输入之外至少两个额外的视图来查看场景背后。
Handling invalid samples
?虽然不同视图的截锥体在大部分情况下重叠,但仍然有可能有光线离开截锥体,从而采样无效的特征或采样无效的颜色。这些无效射线会导致训练过程中的噪声和不稳定。因此,提出了一种检测和删除无效射线的策略,当来自无效采样颜色或特征的对最终聚合颜色的贡献量超过某个阈值τ时,该射线应该被丢弃。考虑一条在位置
x
i
,
i
∈
[
1
,
2
,
…
,
S
]
x_i, i∈[1,2,…,S]
xi?,i∈[1,2,…,S] 处计算的射线。,从第K帧重构得到:
O
i
,
K
,
K
∈
{
I
}
∪
K
O_{i, K}, K∈ \{I\}∪K
Oi,K?,K∈{I}∪K 表示指示函数
x
i
x_i
xi? 在第 K 帧的摄像机视锥之外。注意,总是从输入帧中采样特征。将 IV(k) 定义为表示基于帧 k 渲染的颜色无效的函数,如下所示:
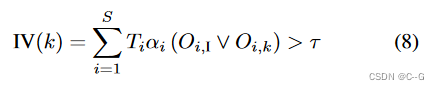
?只有当 IV(k) 对于所有重建射线的帧都为真时,在计算损失值时忽略射线。这背后的原因是,非无效射线仍然会导致最低的误差。因此,式(5)中的min运算将忽略无效射线。
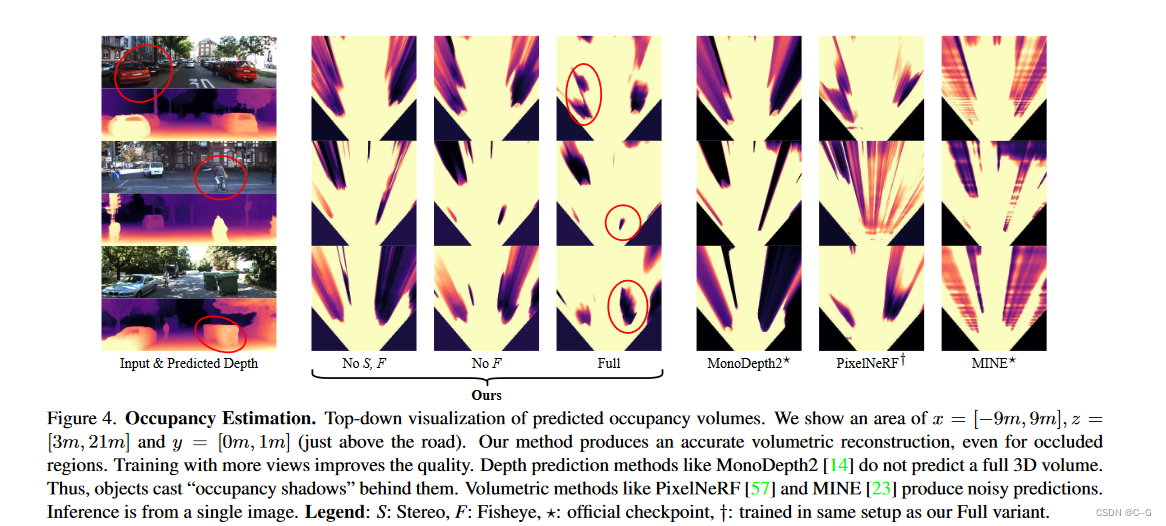
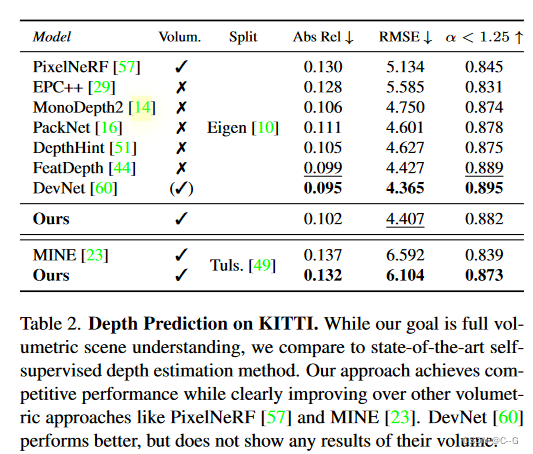
实验

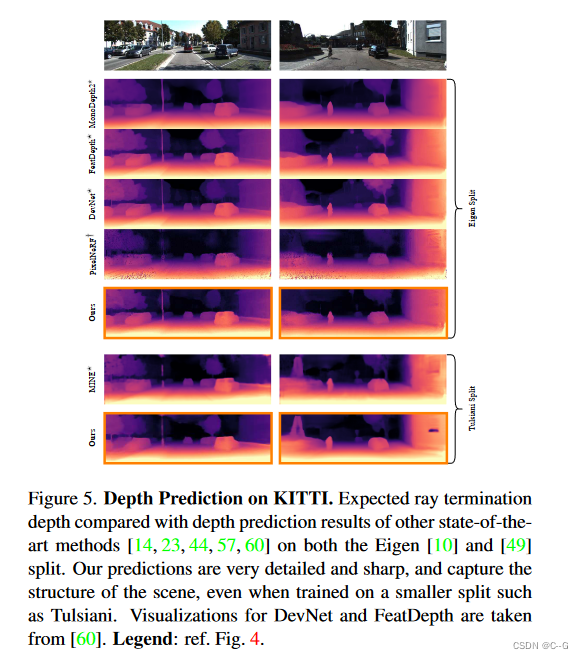


本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- Kafka消息队列设计 - Topic、Partition、Offset分析,并整合Spring Boot项目
- 【新加坡机器人学会支持】第三届工程管理与信息科学国际学术会议 (EMIS 2024)
- 新喜报,新希望!英码科技荣登“2023年广州拟上市领头羊TOP50企业榜单”
- 【深入理解 ByteBuf 之三 接口&类拆解】2. Recycler 接口设计真正的回收机制
- 深入探讨:开发连锁餐饮APP的关键技术要点
- 基于yolov2深度学习网络的车辆检测算法matlab仿真,包括白天场景和夜晚场景
- 后端杂七杂八系列篇三
- FreeRTOS基础知识,教程,简介,框架,手册
- 紫光FPGA学习之常见报错
- 中霖教育:环评工程师是做什么的?

