汉诺塔问题

汉诺塔问题是实践递归的一个典型问题；

问题是：有三根杆子A、B、C，和若干个大小不同的盘子，从杆子A上开始放置盘子，并且规定只能从A、B、C中的一根杆子上把盘子移到另一根杆子上，而且在移动盘子的过程中，每次只能移动一个盘子，并且不能把大的盘子放在小的盘子上面。现在要求把所有的盘子从杆子A移动到杆子C上。

因此可以把A作为起始柱子，B作为中转柱子，C作为终点柱子。

下面是实现的代码（解释在代码里面）

//汉诺塔问题
// 函数声明
void hanoi(int n, char A, char B, char C);

int main()?
{
?? ?int n;
?? ?printf("请输入汉诺塔的层数：");
?? ?scanf("%d", &n);
?? ?//传递参数，A，B，C代表柱子。
?? ?hanoi(n, 'A', 'B', 'C');
?? ?return 0;
}

// 函数定义
void hanoi(int n, char A, char B, char C)?
{
?? ?//若n==1则只需将盘子从A柱（起始）移到C柱子（终点）
?? ?if (n == 1)?
?? ?{
?? ??? ?printf("将第1个盘子从 %c 移到 %c\n", A, C);
?? ?}
?? ?//若n>=2
?? ?else?
?? ?{
?? ??? ?//只需将A柱子上的n-1个盘子借助C柱子移到B柱子
?? ??? ?hanoi(n - 1, A, C, B);
?? ??? ?//再将剩下的第n个盘子移到直接C柱子
?? ??? ?printf("将第%d个盘子从 %c 移到 %c\n", n, A, C);
?? ??? ?//此时B柱子上有n-1个盘子，把B柱子看作起始柱，A柱子看作中转柱，C柱子仍是终点。
?? ??? ?hanoi(n - 1, B, A, C);
?? ?}
}
//这就完成了递归方法写出了汉诺塔问题的答案。

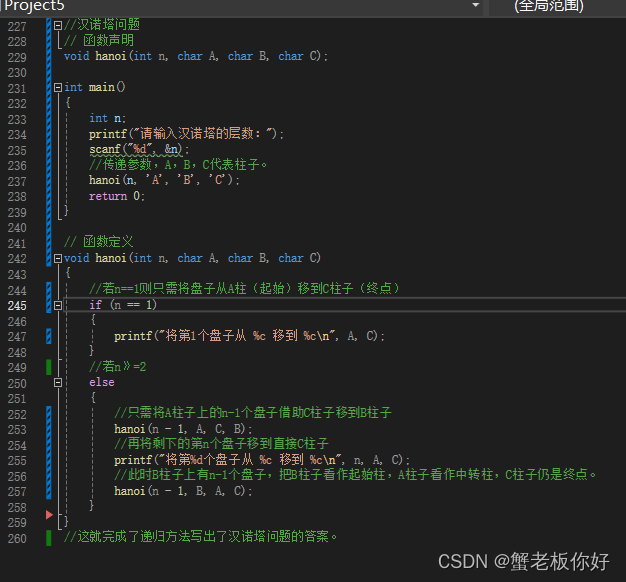
下面是代码截图和盘子为三时的运行结果