【白话机器学习的数学】读书笔记(2)学习回归
二、学习回归
1. y y y与 f θ ( x ) f_\theta(x) fθ?(x)
y y y 是实际数据x对应的值
f θ ( x ) f_\theta(x) fθ?(x)是我们构造出来的函数,例如 f θ ( x ) = θ 0 + θ 1 x f_\theta(x) = \theta_0 + \theta_1 x fθ?(x)=θ0?+θ1?x
所以我们希望这两个越接近,同时我们把 y ? f θ ( x ) y - f_\theta(x) y?fθ?(x)称为误差
2.目标函数
假设有 n 个训练数据,那么它们的误差之和可以用这样的表达式表示。这个表达式称为
目标函数,E(θ)的E是误差的英语单词 Error 的首字母
E
(
θ
)
=
1
2
∑
i
=
1
n
[
y
(
i
)
?
f
θ
(
x
(
i
)
)
]
2
E(\theta) = \frac{1}{2}\sum_{i=1}^n[y^{(i)}-f_\theta(x^{(i)})]^2
E(θ)=21?i=1∑n?[y(i)?fθ?(x(i))]2
找到使 E(θ) 的值最小的 θ。这样的问题称为最优化问题。
3.最小二乘法
修改 θ \theta θ使得 E ( θ ) E(\theta) E(θ)越来越小,这种做法成为最小二乘法。
4.最速下降法
要让 E(θ) 越来越小,一边随意修改 θ 的值,一边计算 E(θ) 并与之前的值相比较的做法实在是太麻烦了。
微分是计算变化的快慢程度时使用的方法。
书中举了一个例子:
g
(
x
)
=
x
2
?
2
x
+
1
d
g
(
x
)
d
x
=
2
x
?
2
g(x) = x^2 - 2x + 1 \\ \frac{dg(x)}{dx} = 2x-2
g(x)=x2?2x+1dxdg(x)?=2x?2
- 增减表

-
图像
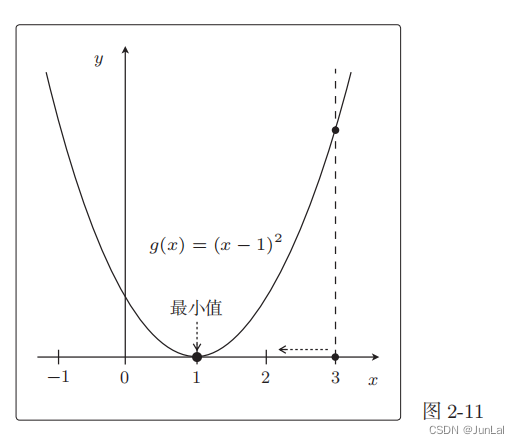
比如在 x = 3 这一点,为了使 g(x)的值变小,我们需要向左移动x,也就是必须减小 x。
只要向与导数的符号相反的方向移动 x,g(x) 就会自然而然地沿着最小值的方向前进了。
最速下降法或梯度下降法
x
:
=
x
?
η
d
g
(
x
)
d
x
x:=x - \eta \frac{dg(x)}{dx}
x:=x?ηdxdg(x)?
- η \eta η称为学习率的常数
- A:=B,就是用B来定义A
这个同样适用于目标函数(目标函数也是个开口向上的)
θ
0
:
=
θ
0
?
η
?
E
?
θ
0
θ
1
:
=
θ
1
?
η
?
E
?
θ
1
\theta_0 := \theta_0 - \eta \frac{\partial E}{\partial \theta_0} \\ \theta_1 := \theta_1 - \eta \frac{\partial E}{\partial \theta_1}
θ0?:=θ0??η?θ0??E?θ1?:=θ1??η?θ1??E?
复合函数的微分
u
=
E
(
θ
)
v
=
f
θ
(
x
)
?
u
?
θ
0
=
?
u
?
v
?
?
v
?
θ
0
u = E(\theta)\\ v=f_\theta(x)\\ \frac{\partial u}{\partial \theta_0} = \frac{\partial u}{\partial v} ·\frac{\partial v}{\partial \theta_0}
u=E(θ)v=fθ?(x)?θ0??u?=?v?u???θ0??v?
其中
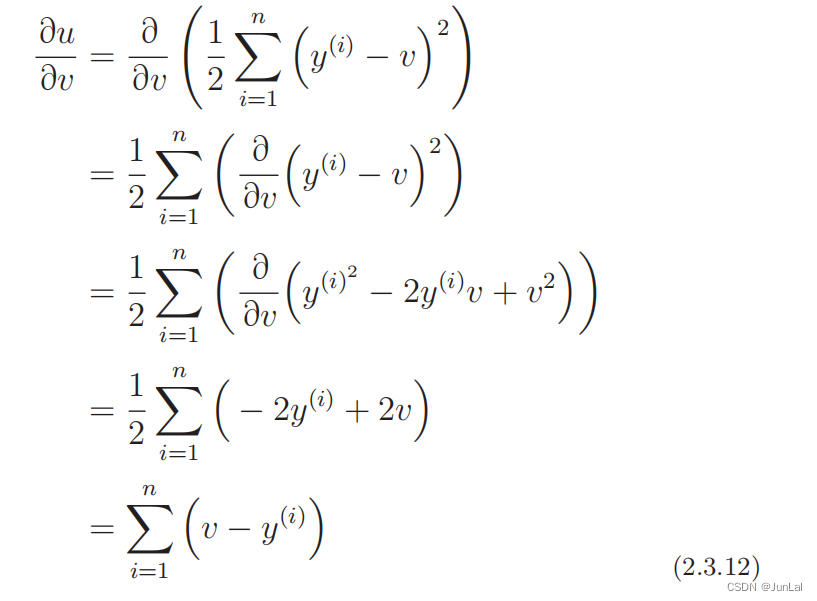
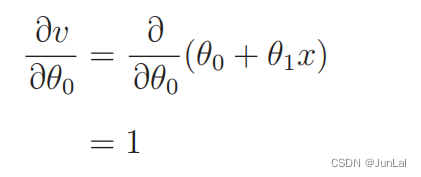
所以有
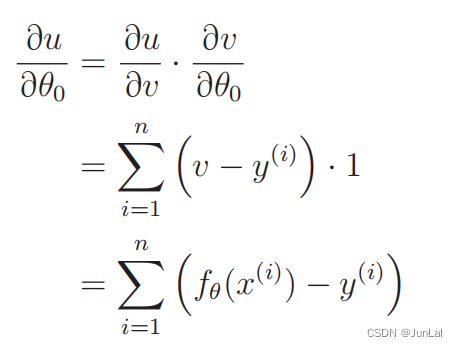
同理可以得到 ? u ? θ 1 \frac{\partial u}{\partial \theta_1} ?θ1??u?
所以最终可以得到
θ
0
:
=
θ
0
?
η
?
E
?
θ
0
=
θ
0
?
η
∑
i
=
1
n
[
f
θ
(
x
(
i
)
?
y
(
i
)
)
]
θ
1
:
=
θ
1
?
η
?
E
?
θ
1
=
θ
0
?
η
∑
i
=
1
n
[
f
θ
(
x
(
i
)
?
y
(
i
)
)
]
x
(
i
)
\theta_0 := \theta_0 - \eta \frac{\partial E}{\partial \theta_0} = \theta_0 - \eta\sum_{i=1}^n[f_\theta(x^{(i)} - y^{(i)})] \\ \theta_1 := \theta_1 - \eta \frac{\partial E}{\partial \theta_1} = \theta_0 - \eta\sum_{i=1}^n[f_\theta(x^{(i)} - y^{(i)})]x^{(i)}
θ0?:=θ0??η?θ0??E?=θ0??ηi=1∑n?[fθ?(x(i)?y(i))]θ1?:=θ1??η?θ1??E?=θ0??ηi=1∑n?[fθ?(x(i)?y(i))]x(i)
根据这个表达式来更新
θ
0
\theta_0
θ0?和
θ
1
\theta_1
θ1?,就可以找到好的一次函数
f
θ
(
x
)
f_\theta(x)
fθ?(x)
缺点:
- 计算量大
- 计算时间长
- 容易陷入局部最优解
5.多项式回归
将一次函数拓展为多次函数,即
f
θ
(
x
)
=
θ
0
+
θ
1
x
→
f
θ
(
x
)
=
θ
0
+
θ
1
x
+
θ
2
x
2
+
.
.
.
+
θ
n
x
n
f_\theta(x) = \theta_0 + \theta_1 x \to f_\theta(x) = \theta_0 + \theta_1 x +\theta_2x^2+...+\theta_nx^n
fθ?(x)=θ0?+θ1?x→fθ?(x)=θ0?+θ1?x+θ2?x2+...+θn?xn
同理,对于
θ
n
\theta_n
θn?的更新规则也和最速下降法中一样
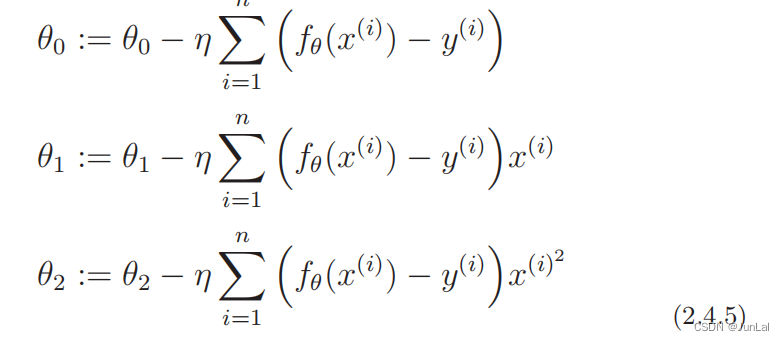
6.多重回归
将一次函数中的x变为多个x,即
f
θ
(
x
)
=
θ
0
+
θ
1
x
→
f
θ
(
x
1
,
x
2
,
.
.
.
,
x
n
)
=
θ
0
+
θ
1
x
1
+
.
.
.
+
θ
n
x
n
f_\theta(x) = \theta_0 + \theta_1 x \to f_\theta(x_1,x_2,...,x_n) = \theta_0 + \theta_1 x_1 + ...+ \theta_n x_n
fθ?(x)=θ0?+θ1?x→fθ?(x1?,x2?,...,xn?)=θ0?+θ1?x1?+...+θn?xn?
然后为了方便,我们可以用向量来表示
θ
=
[
θ
0
θ
1
.
.
.
θ
n
]
,
x
=
[
1
x
1
.
.
.
x
n
]
(2)
\theta = \begin{bmatrix} \theta_0\\ \theta_1\\ ...\\ \theta_n \end{bmatrix} \tag{2} , x = \begin{bmatrix} 1\\ x_1\\ ...\\ x_n \end{bmatrix}
θ=
?θ0?θ1?...θn??
?,x=
?1x1?...xn??
?(2)
对应的
f
θ
(
x
)
=
θ
T
x
=
θ
0
+
θ
1
x
+
θ
2
x
2
+
.
.
.
+
θ
n
x
n
f_\theta(x) = \theta^Tx = \theta_0 + \theta_1 x +\theta_2x^2+...+\theta_nx^n
fθ?(x)=θTx=θ0?+θ1?x+θ2?x2+...+θn?xn
要求出合适的更新规则,其实也和前面的做法一样,复合函数求微分
u
=
E
(
θ
)
v
=
f
θ
(
x
)
?
u
?
θ
j
=
?
u
?
v
?
?
v
?
θ
j
u = E(\theta)\\ v=f_\theta(x)\\ \frac{\partial u}{\partial \theta_j} = \frac{\partial u}{\partial v} ·\frac{\partial v}{\partial \theta_j}
u=E(θ)v=fθ?(x)?θj??u?=?v?u???θj??v?
所以
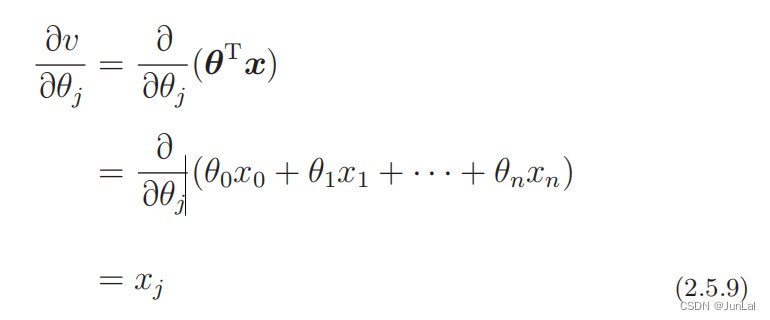
对应的第j个参数的更新表达式为
θ
j
:
=
θ
j
?
η
∑
i
=
1
n
[
f
θ
(
x
(
i
)
?
y
(
i
)
)
]
x
j
(
i
)
\theta_j := \theta_j - \eta\sum_{i=1}^n[f_\theta(x^{(i)} - y^{(i)})]x_j^{(i)}
θj?:=θj??ηi=1∑n?[fθ?(x(i)?y(i))]xj(i)?
7.随机梯度下降法
最速下降法的参数更新表达式
θ
j
:
=
θ
j
?
η
∑
i
=
1
n
[
f
θ
(
x
(
i
)
?
y
(
i
)
)
]
x
j
(
i
)
\theta_j := \theta_j - \eta\sum_{i=1}^n[f_\theta(x^{(i)} - y^{(i)})]x_j^{(i)}
θj?:=θj??ηi=1∑n?[fθ?(x(i)?y(i))]xj(i)?
这个表达式使用了所有训练数据的误差,而在随机梯度下降法中会随机选择一个训练数据,并使用它来更新参数。这个表达式中的 k 就是被随机选中的数据索引。
θ
j
:
=
θ
j
?
η
[
f
θ
(
x
(
k
)
?
y
(
k
)
)
]
x
j
(
k
)
\theta_j := \theta_j - \eta[f_\theta(x^{(k)} - y^{(k)})]x_j^{(k)}
θj?:=θj??η[fθ?(x(k)?y(k))]xj(k)?
因此,最速下降法更新 1 次参数的时间,随机梯度下降法可以更新 n 次。
此外,随机梯度下降法由于训练数据是随机选择的,更新参数时使用的又是选择数据时的梯度,所以不容易陷入目标函数的局部最优解。
8.小批量梯度下降法
这个方法介于最速下降法和随机梯度下降法之间的方法。
-
最速下降法是用了全部的训练数据
-
随机梯度下降法是只用了一个数据。
-
小批量梯度下降法就是选择部分的数据。
假设训练数据有 100 个,那么在 m = 10 时,创建一个有 10 个随机数的索引的集合,例如 K = {61, 53, 59, 16, 30, 21, 85, 31, 51, 10}、
对应的更新规则为
θ
j
:
=
θ
j
?
η
∑
k
∈
K
[
f
θ
(
x
(
k
)
?
y
(
k
)
)
]
x
j
(
k
)
\theta_j := \theta_j - \eta\sum_{k\in K}[f_\theta(x^{(k)} - y^{(k)})]x_j^{(k)}
θj?:=θj??ηk∈K∑?[fθ?(x(k)?y(k))]xj(k)?
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- DALLE·3的图片一致性火了!
- 基础数据结构练习(栈)
- 日志系统二(ilogtail+kafka+logstash+es+kibana)
- 【总结】浅谈深度学习算法与硬件协同优化
- 数据结构初阶之排序
- Python游戏开发实战:经典游戏制作教程
- 要笑疯了,老师剪掉寒假作业上的答案二维码!
- 2023 我的编程之旅——路人贾‘ω‘
- 关于uvm_reg_predictor #() predictor
- 如何引用R语言版本以及R包版本