【Leetcode 程序员面试金典 02.08】 —— 环路检测 |双指针

面试题02.08. 环路检测

给定一个链表，如果它是有环链表，实现一个算法返回环路的开头节点。若环不存在，请返回null。

如果链表中有某个节点，可以通过连续跟踪next指针再次到达，则链表中存在环。 为了表示给定链表中的环，我们使用整数pos来表示链表尾连接到链表中的位置（索引从 0 开始）。 如果pos是 -1，则在该链表中没有环。注意：pos不作为参数进行传递，仅仅是为了标识链表的实际情况。

题目分析

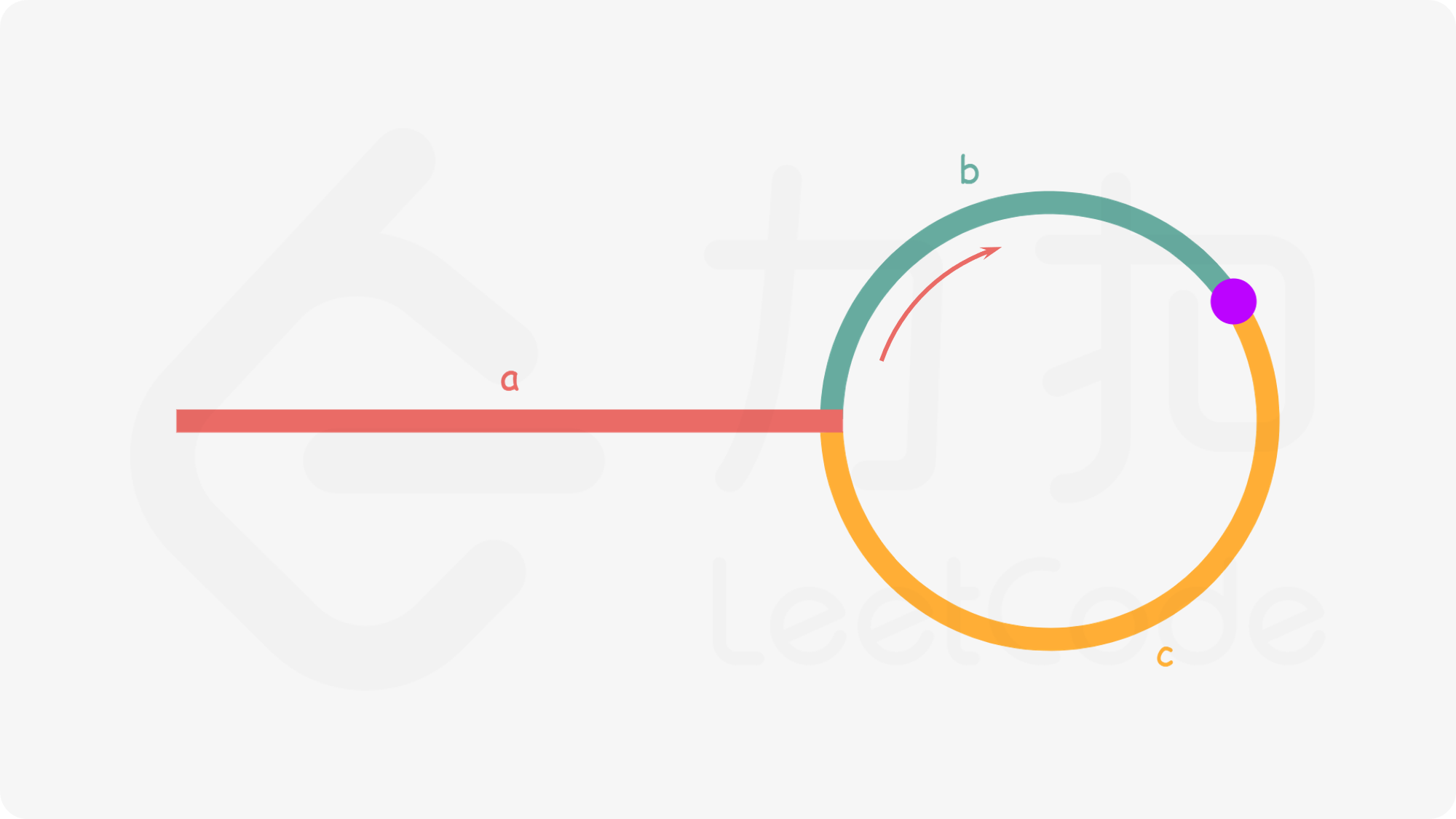
我们可以使用双指针解决本题

快指针走了：$a+(b+c)m+b$
慢指针走了：$a+(b+c)n+b$
根据快走的是慢的两倍，
$a+(b+c)m+b=2(a+(b+c)n+b)$ =>
$a=(b+c)(m?2n)?b$

得 a 的距离为（环长度的倍数 - b），即 tmp 指针从头节点走到环开头节点等于 slow 指针走到环开头节点的距离

双指针顾名思义，就是同时使用两个指针，在序列、链表结构上指向的是位置，在树、图结构中指向的是节点，通过或同向移动，或相向移动来维护、统计信息

经典双指针的数组遍历，更多案例可见 Leetcode 双指针详解

/**
 * Definition for singly-linked list.
 * class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */
public class Solution {
    public ListNode detectCycle(ListNode head) {
        if(head == null){
            return null;
        }

        ListNode slow = head, fast = head;
        while(fast != null){
            slow = slow.next;
            if(fast.next != null){
                fast = fast.next.next;
            } else {
                return null;
            }

            if(slow == fast){
                ListNode tmp = head;
                while(tmp != slow){
                    tmp = tmp.next;
                    slow = slow.next;
                }
                return tmp;
            }
        }
        return null;
    }
}