C++ 递归函数 详细解析——C++日常学习随笔
发布时间:2023年12月31日
1. 递归函数
1.1 递归函数的定义
-
递归函数:即在函数体中出现调用自身的函数,即函数Func(Type a,……)直接或间接调用函数本身;
-
递归函数:在数学上,关于递归函数的定义如下:对于某一函数f(x),其定义域是集合A,那么若对于A集合中的某一个值x0,其函数值f(x0)由f(f(x0))决定,那么就称f(x)为递归函数;
-
递归函数:不能定义为内联函数;
1.2 递归的本质
递归函数的例子:
(1)例子一:等差数列
数列1 3 5 7 9……代码实现输入一个数n,输出数列第n项的值。
#include<iostream>
using namespace std;
int f(int n)
{
if(n==1)
return 1;
else
return f(n-1)+2;
}
int main()
{
int n;
cin >> n;
cout << f(n);
return 0;
}解释:递归关系:f(n-1)+2,递归出口:1;?
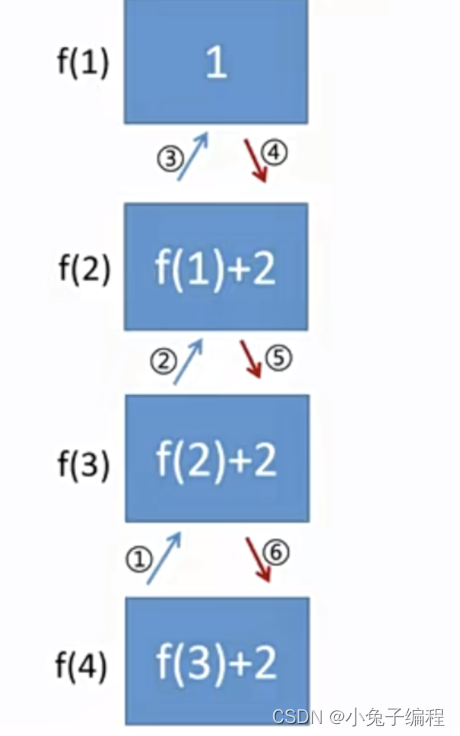 ?
?
(2)例子二:阶乘n!
递归的数学函数描述:
f(n)=1 (n=1)
f(n)=n*f(n-1) (n>1)递归的C++函数描述:
int f(nt n)
{
if(n==1)
return 1;
return n*f(n-1);
}注:由于f(13)>2^32。所以对于int型(无符号类型)的表示范围,其n的取值范围只有1<=n<=12了。
(3)例子3:Fibonacci数列
斐波那契数列:1,1,2,3,5,8,13,21,34,55,89…
递归的数学函数描述:
f(n)=0 (n=0)
f(n)=1 (n=1)
f(n)=f(n-1)+f(n-2) (n>2)递归的C++函数描述:
int f(int n)
{
if((n==0) || (n==1))
return n;
return f(n-1)+f(n-2) ;
}#include<iostream>
using namespace std;
int f(int n)
{
if(n==1||n==2)
return 1;
else
return f(n-1)+f(n-2);
}
int main()
{
int n;
cin>>n;
cout<<f(n);
return 0;
}(4)例子4:王小刀切饼:
王小二自夸刀工不错,有人放一张大的煎饼在砧板上,问他:“饼不许离开贴板,切n(1<=n<=100)刀最多能分成几块?
输入格式:输入切的刀数n
输出格式:输出切n刀最多切的块数
#include<iostream>
using namespace std;
int f(int n)
{
if(n==1)
return 2;
else
return f(n-1)+n;
}
int main()
{
int n;
cin>>n;
cout<<f(n);
return 0;
}解释:递归关系:f(n-1)+n,递归出口:n=1;
先列举几项就会发现规律
第一刀2
第二刀2+2=4
第三刀 4+3=7
第四刀 7+4=11
……
第n-1刀 i
第n刀 i+n
如图

(5)例子5:杨辉三角

#include<iostream>
using namespace std;
int f(int x,int y)
{
if(y==0||x==y)
return 1;
else
return f(x-1,y-1)+f(x-1,y);
}
int main()
{
int x,y;
cin>>x>>y;
cout<<f(x,y);
return 0;
}(6)例子6:最大公约数?
#include<iostream>
using namespace std;
int gcd(int a,int b)
{
int r=a%b;
if(r==0) return b;
return gcd(b,r);
}
int main()
{
int m,n;
cin>>m>>n;
cout<<gcd(m,n);
return 0;
}解释:
辗转相除法又名欧几里得算法,目的是求出两个正整数的最大公约数。它是最古老的算法,其可追溯刀公元前300年前。
这条算法基于一个定理:两个正整数a和b(a>b),他们的最大公约数等于a除以b的余数c和较小数b之间的最大公约数。
?
- 递归有直接递归和间接递归之分:
- 直接递归:直接调用函数本身;
- 间接递归:指函数体中没有直接调用自身函数,而是调用了另一个函数,在那个函数里,出现了调用本函数的语句。或者,在那个函数里,又调用了一个其他函数,反复出现调用其它函数,而最后有一个函数调用了本函数;
- 注:递归函数在运行中,其调用与被调用函数的指令代码是同一个函数副本,只不过各个不同运行中的调用点作为状态的一部分,在栈中被分别保护了起来。因此,是C++的函数机制决定了递归操作中的数据独立性,因而使递归调用成为可能。
1.3 递归条件
- 递归不能无限制地调用下去,因为栈空间是有限的。所以递归函数是有条件地调用自身,该条件就是递归的停止条件;
- 递归函数中必须有完成终极任务的语句序列(如:return 1;),以使函数有意义,递归调用,并非终极;
- 递归函数当然有递归调用语句,递归调用应有参数,而且参数值应该是逐渐逼近停止条件;
- 递归条件应先测试,后递归调用,无条件递推的逻辑错误,编译器是检查不出来的,要靠程序员自己把握;
- 注:消去递归,即大多数递归函数都能用非递归函数来替代,一般用循环语句实现。?
1.4 递归函数的优缺点
优点:
- 简化程序设计,使程序易读;
- 作为对特殊问题的一种处理方法,递归仍然占有一席之地;
- 许多高难算法的简捷描述,往往采用递归,特别对于能较快逼近停止条件的、优化了的递归函数;
- 递归在迅速退栈的技术处理上得到了异常机制的帮助;
缺点:
- 递归会迅速递增系统开销;
- 在时间上,执行函数的调用与返回的次数明显要大于非递归函数;
- 在空间上,栈空间资源会遭到空前的劫掠,随着每递归一次,栈内存就会多占用一截;
文章来源:https://blog.csdn.net/frank2102/article/details/135313171
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 计算机毕业设计 基于MVC的自习室管理和预约系统的设计与实现 Java实战项目 附源码+文档+视频讲解
- Jmeter入门教程
- 【Java集合篇】ConcurrentHashMap是如何保证线程安全的
- 基于SURF算法的图像匹配
- x-cmd pkg | fx - Warp 支持的 JSON 查看和处理工具
- STL之set
- OFDM系统信道估计误码率matlab仿真,对比LS,LMMSE,LR-LMMSE三种信道估计算法
- 集帅集美们都在看的MySQL详细安装教程~
- 力扣刷MySQL-第六弹(详细讲解)
- ssm爱心互助及物品回收管理系统(开题+源码)