刷题 ------ 枚举

这篇博客和上篇一样，既然叫成枚举，那么在做题上也大多采用了暴力枚举的方式去做的，有些更有效的方式也没有去写

1.统计好三元组

• 嗯，，，，直接三重for循环搞定了吧。
• 注意如果前两个 i 和 j 已经不满足了，k就没有继续下去的必要了

int countGoodTriplets(int* arr, int arrSize, int a, int b, int c)
{
    int i,j,k,ans = 0;
    for (i = 0; i < arrSize - 2; i++)
    {
        for (j = i + 1; j < arrSize - 1; j++)
        {
            //前俩下标和已经不满足了，后面的就没有必要进行了
            if(abs(arr[i] - arr[j]) > a)
            {
                continue;
            }
            for (k = j + 1; k < arrSize; k++)
            {
                if(abs(arr[j] - arr[k]) <= b && abs(arr[i] - arr[k]) <= c)
                {
                    ans++;
                }
            }
        }
    }
    return ans;
}

2.重复至少k次且长度为M的模式

上篇博客中所解题方式是模拟，这题同样也可以模拟出来。

• 遍历所有的情况！！

//比较俩数组是否相同
bool Compare(int* nums1, int* nums2, int numsSize)
{
    int i;
    for (i = 0; i < numsSize; i++)
    {
        if(nums1[i] != nums2[i])
        {
            return false;
        }
    }

    return true;
}


bool containsPattern(int* arr, int arrSize, int m, int k)
{
    int left,right,count = 0;;
    int* tmp = (int*)calloc(m, sizeof(int));
    for (int i = 0; i < arrSize - 1; i++)
    {
        for (left = i,right = left + m - 1; right < arrSize; left += m,right += m)
        {
            if(Compare(tmp,arr + left,m))
            {
                count++;
                if(count == k)
                {
                    return true;
                }
            }
            else
            {
                //重置次数，更新数组
                memcpy(tmp,arr + left,sizeof(int) * m);
                count = 1;
            }
        }
        //将tmp数组清空
        memset(tmp,0,sizeof(int) * m);
    }

    return false;
}

• 下面这种方法，牛的，
• 我感觉它的精髓就在 arr[i + j] != arr[i + j % m] 这一句话

bool containsPattern(int* arr, int arrSize, int m, int k)
{
    int i,j;
    for (i = 0; i <= arrSize - m * k;i++)
    {
        //
        for (j = 0; j < m*k; j++)
        {
            if(arr[i + j] != arr[i + j % m])
            {
                break;
            }
        }
        //提前出来的话就证明前后不相同，
        if(j == m*k)
        {
            //j全部走完了，就证明全部相等
            return true;
        }
    }

    return false;
}

3.统计平方和三元数组数目

• 这题肯定也可以使用三层for循环来解决这个。
• 但是时间上肯定是不快的，我们可以利用C语言的pow和sqrt函数来帮助实现。
  
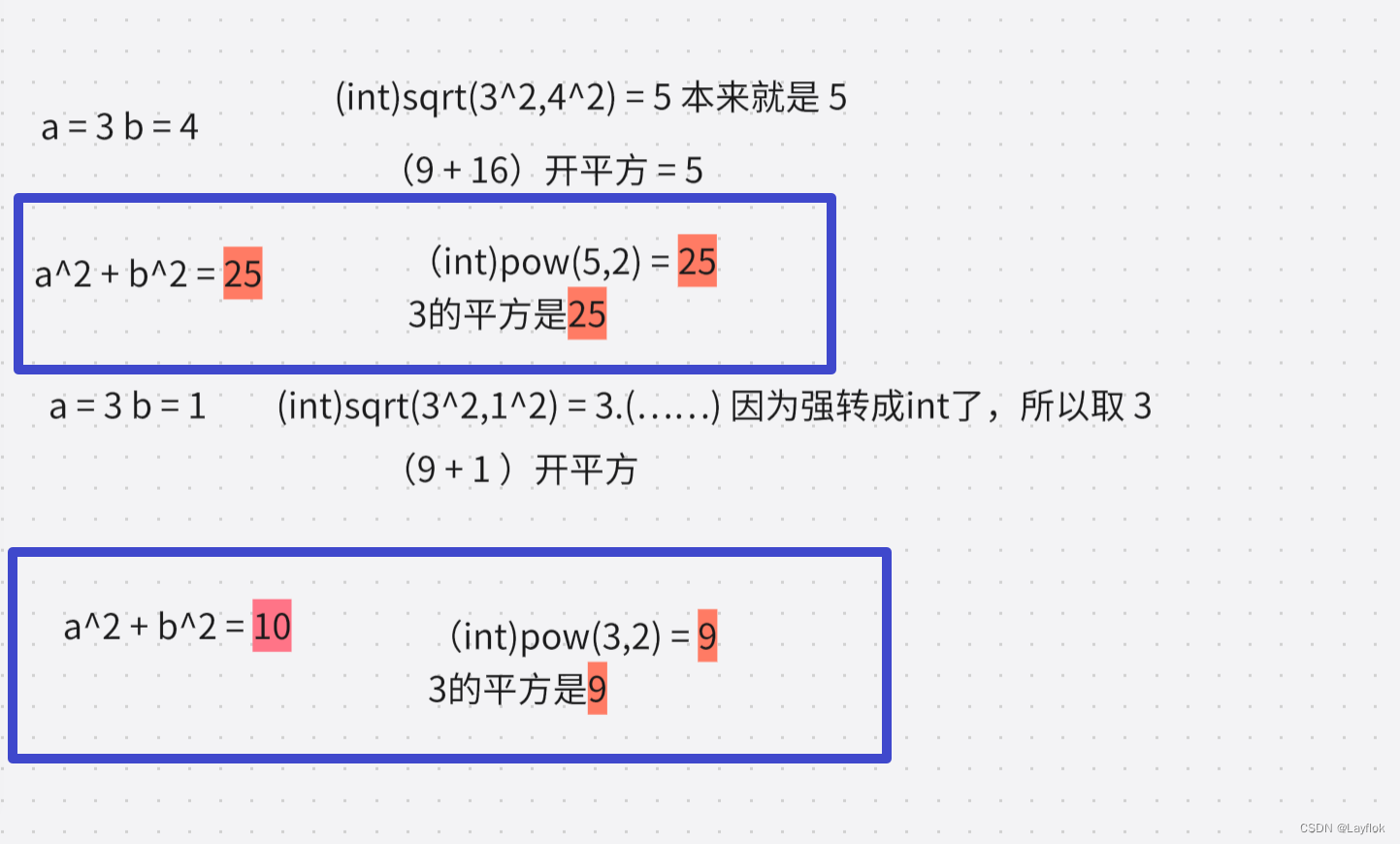
  上图中两个a和b可以看出来,就是一个精确，一个不精确的意思

int countTriples(int n)
{
    int a,b,c,ans = 0;
    for (a = 3; a < n; a ++)
    {
        for (b = 1; b < n; b++)
        {
            if(a*a + b*b <= n*n)
            {
                if(a*a + b*b == (int)pow((int)sqrt(a*a+b*b),2))
                {
                    ans++;
                }
            }
        }
    }    

    return ans;
}

4.统计特殊四元组

• 直接枚举，四层for循环就能做出来。

int countQuadruplets(int* nums, int numsSize)
{
    int a,b,c,d,ans = 0;
    for (a = 0; a < numsSize-3; a++)
    {
        for (b = a + 1; b < numsSize-2; b++)
        {
            for (c = b + 1; c < numsSize-1; c++)
            {
                for (d = c + 1; d < numsSize; d++)
                {
                    if(nums[a] + nums[b] + nums[c] == nums[d])
                    {
                        ans++;
                    }
                }
            }
        }
    }

    return ans;
}

• 也可以利用哈希表，这样可以减少一层for循环
• 因为要满足 a < b < c < d 这样一个条件，
• 所以可以倒着遍历。

int countQuadruplets(int* nums, int numsSize)
{
    int map[10000] = {0};
    int a,b,c,ans = 0;
    for (c = numsSize - 2; c >= 2; c--)
    {
        map[nums[c+1]]++;
        for (a = 0; a < c; a++)
        {
            for (b = a + 1; b < c; b++)
            {
                ans += map[nums[a] + nums[b] + nums[c]];
            }
        }
    }

    return ans;
}

5. 找出3为偶数

• 枚举所有的数
• 首位不能是0
• 中间随便，但是不能用首位用过的数
• 末尾只能是偶数，这样才能保证整体是偶数，但是不能用前两位用过的数。

#define MAX_SIZE 100000

/**
 * Note: The returned array must be malloced, assume caller calls free().
 */

int cmp_int(const void* x, const void* y)
{
    return *(int*)x - *(int*)y;
}


int* findEvenNumbers(int* digits, int digitsSize, int* returnSize)
{
    int i,j,k;
    int map[1000] = {0};
    int* ans = (int*)malloc(sizeof(int) * MAX_SIZE);
    int size = 0;
    for (i = 0; i < digitsSize; i++)
    {
        //首位不能是 0 
        if(digits[i] != 0)
        {
            //中间
            for (j = 0; j < digitsSize; j++)
            {
                //不能重复使用一个数字
                if(j == i)
                {
                    continue;
                }
                //末尾
                for(k = 0; k < digitsSize; k++)
                {
                    //不能重复，并且不能是奇数
                    if(k == i || k == j || digits[k] % 2 != 0)
                    {
                        continue;
                    }
                    int num = digits[i] * 100 + digits[j] * 10 + digits[k];
                    //如果出现过就不用再去录入了
                    if(map[num] == 0)
                    {
                        map[num]++;
                        ans[size++] = num;
                    }
                }

            }
        }
    }
    qsort(ans,size,sizeof(ans[0]),cmp_int);
    *returnSize = size;
    return ans;
}

6.移除指定数字得到的最大结果

• 可以直接枚举出所有的结果，然后去比较哪一个构造出来的更大，从而选择返回哪一个即可

char* removeDigit(char* number, char digit)
{
    int i,len = strlen(number);
    char* ans = (char*)malloc(sizeof(char) * len);
    char* tmp = (char*)malloc(sizeof(char*) * len);
    ans[0] = '\0';
    tmp[0] = '\0';
    for (i = 0; i < len; i++)
    {
        //求出所有可能行
        if(number[i] == digit)
        {
            //前面
            memcpy(tmp,number,sizeof(char) * i);
            //后面
            memcpy(tmp+i,number + i + 1,sizeof(char) * len - i- 1);
            tmp[len-1] = '\0';
            //（判断选择哪一个）新构造出来的比原来的大
            if(strcmp(tmp,ans) > 0)
            {
                strcpy(ans,tmp);
            }
        }
    }
    
    return ans;
}

• 还有一种办法，不需要这么麻烦，
• 找到所需要删除的字符，然后这个字符比后一个位置小，那么这就是那个需要删除的下标.

char* removeDigit(char* number, char digit)
{
    int i, len = strlen(number),index = 0;
    for (i = 0; i < len; i++)
    {
        if(number[i] == digit)
        {
            //找到下标
            index = i;
            if(number[i] < number[i + 1])
            {
                //找到合适的下标，当前的这个比后一个要小。
                break;
            }
        }
    }

    for (i = index; i < len; i++)
    {
        number[i] = number[i  + 1];
    }
    
    return number;
}

7. 兼具大小写的最好英文字母

• 拿两个哈希表来分别记录各个大写字母和小写字母出现的次数。
• 然后从后往前遍历，如果有一个字母大小写同时出现，那么就是它了。

char* greatestLetter(char* s)
{
    char* ans = (char*)malloc(sizeof(char) * 2);
    ans[0] = '\0';
    int mapSmall[26] = {0};
    int mapBig[26] = {0};
    int i, len = strlen(s);
    for (i = 0; i < len; i++)
    {
        if(s[i] >= 'a' && s[i] <= 'z')
        {
            mapSmall[s[i] - 'a']++;
        }
        else
        {
            //大写
            mapBig[s[i] - 'A']++;
        }
    }

    for (i = 25 ; i >= 0; i--)
    {
        //大写出现过
        if(mapBig[i] != 0 && mapSmall[i] !=0 )
        {
            ans[0] = i + 65;
            ans[1] = '\0';
            return ans;
        }
    }

    return ans;
}

8. 算术三元组的数目

• 因为nums[k] - nums[j] == diff , nums[j] - nums[i]
• 所以，可以先确保 j 是满足于 k 的情况下，再去判断 i 是多少

int arithmeticTriplets(int* nums, int numsSize, int diff)
{
    int i,j,k,ans = 0;
    for (k = numsSize-1; k >=  2; k--)
    {
        for (j = k - 1; j >= 1; j--)
        {
            //这样的话就能确定 j 是正确的了
            if(nums[k] - nums[j] == diff)
            {
                for (i = j - 1; i >= 0; i--)
                {
                    if(nums[j] - nums[i] == diff)
                    {
                        ans++;
                    } 
                }
            }
            
        }
    } 

    return ans;
}

9.公因子的数目

• 嗯。。。。。怎么说
• 选择出两个数中最小的那个数，然后从遍历到那个数，判断是否能将a 和 b同时模到 0 的就是

int commonFactors(int a, int b)
{
    int ans = 1;
    int min = a > b ? b : a;
    for (int i = 2; i <= min; i++)
    {
        if(a % i == 0 && b % i == 0)
        {
            ans++;
        }
    }


    return ans;    
}

10.有效的时间数目

• 下面注释中有写特殊的例子

int countTime(char* time)
{
    char a = time[0],b = time[1],c = time[3],d = time[4];
    int ans = 1;
    if(d == '?')
    {
        ans *= 10;
    }

    if(c == '?')
    {
        ans *= 6;
    }

    if(a == '?' && b == '?')
    {
        ans *= 24;
    }
    else if(a == '?')
    {
        if(b < '4')
        {
            //0~3
            //01 02 03 
            //11 12 13
            //21 22 23
            //31 ERROR
            ans *= 3;
        }
        else
        {
            //0~1
            ans *= 2;
        }
    }
    else if(b == '?')
    {
        if(a == '2')
        {
            //0~3
            //20 21 22 23
            ans *= 4;
        }
        else
        {
            //0~9
            ans *= 10;
        }
    }
    else
    {
        ans *= 1;
    }
    
    return ans;
}

11.从两个数字数组里生成最小的数字

• 求出两个数组中出现相同的数字（如果有多个，选择最小的）可以用哈希表来做
• 如果没有相同的，那么就算了呗，哈哈哈。
• 然后在找出两个数组中那两个最小的值所构造出来的数字
• 使min值与same值去比较，哪一个小，选择哪一个。

int Same(int* nums1, int nums1Size, int* nums2, int nums2Size)
{
    int map[10] = {0};
    int i;
    for (i = 0; i < nums1Size; i++)
    {
        map[nums1[i]]++;
    }
    for (i = 0; i < nums2Size; i++)
    {
        map[nums2[i]]++;
    }
    for (i = 0; i < 10; i++)
    {
        if(map[i] == 2)
        {
            return i;
        }
    }

    return INT_MAX;
}


int minNumber(int* nums1, int nums1Size, int* nums2, int nums2Size)
{
    int ans = 0,i;
    int min1 = nums1[0];
    int min2 = nums2[0];
    //求出相同的数  如果有返回，没有返回一个大值
    int same = Same(nums1,nums1Size,nums2,nums2Size);
    printf("%d\n",same);
    //找出两个数组中最小的值
    for (i = 1; i < nums1Size; i++)
    {
        if(min1 > nums1[i])
        {
            min1 = nums1[i];
        }
    }   
    for (i = 1; i < nums2Size; i++)
    {
        if(min2 > nums2[i])
        {
            min2 = nums2[i];
        }
    }
    //使min1永远最小
    if(min1 > min2)
    {
        int tmp = min2;
        min2 = min1;
        min1 = tmp;
    }
    ans = min1*10 + min2;

    if(same < ans)
    {
        return same;
    }

    return ans;
}

12.最长的交替子序列

• 我这边的默认长度是1，方便计算子序列的长度，可是如果最后长度还是1的话，记得返回-1
• 还有就是判断一曾一减的公式 -1^（j + 1）
• i 每次变化后，j永远是从1开始，就相当于，将(nums+i)看成一个新的数组的其实位置。
  

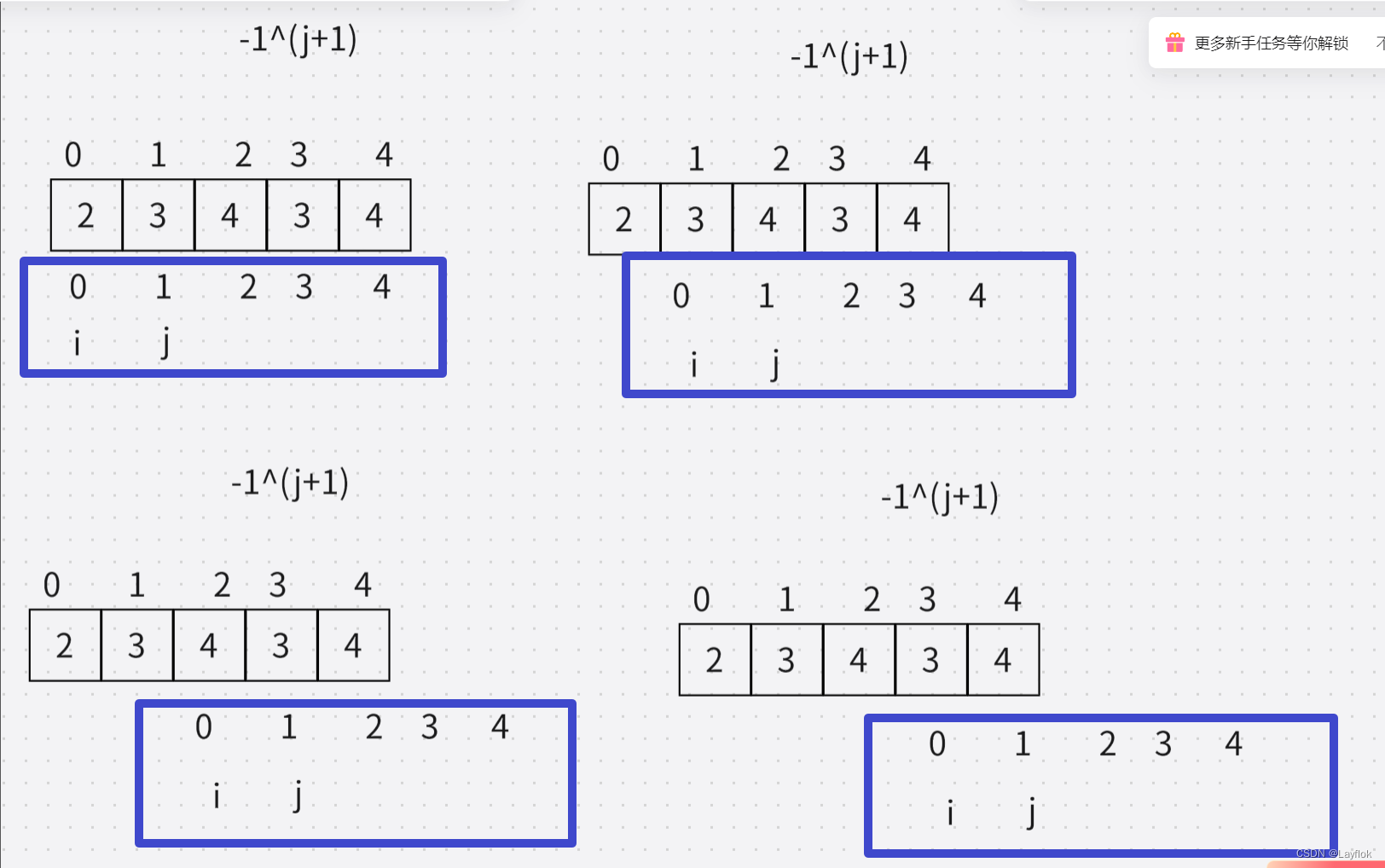
13.特殊元素平方和

• 额。。。。这题没得说，第一个元素的下标还是0.。

int sumOfSquares(int* nums, int numsSize)
{
    int i,ans = 0;
    for (i = 0; i < numsSize; i++)
    {
        if(numsSize % (i+1) == 0)
        {
            ans += nums[i] * nums[i];
        }
    }

    return ans;
}

14.统计对称整数的数目

• 这道题，首先得回拆分一个整数，得到它的每一位。
• 然后将左边位数和和右边的位数和进行比较。

bool Helper(int num)
{
    //1.先求位数
    int n = 0;// n ~ 位数
    int tmp = num;
    while(tmp != 0)
    {
        tmp /= 10;
        n++;
    }
    //如果位数是奇数，一定不会平分对称的
    if(n % 2 != 0)
    {
        return false;
    }

    //2.利用sum1 和 sum2 分别求出右边和左边的总和
    int rightSum = 0,leftSum = 0;
    int count = n / 2;
    while(count != 0)
    {
        //右边
        rightSum += num % 10;
        num /= 10;
        count--;
    }
    count = n / 2;
    while(count != 0)
    {
        //左边
        leftSum += num % 10;
        num /= 10;
        count--;
    }

    //判断
    if(rightSum == leftSum)
    {
        return true;
    }

    return false;
}


int countSymmetricIntegers(int low, int high)
{
    int ans = 0;
    while(low <= high)
    {
        if(Helper(low))
        {
            ans++;
        }
        low++;
    }


    return ans;
}

15.给小朋友们分糖果

• 就这道题直接三层for肯定是ok的。
• 但也可以利用一个数组来表示三个孩子，然后一一给他们分糖果，记录其条件满足的次数即可

int distributeCandies(int n, int limit)
{
    int childern[3] = {0};
    int i,j,ans = 0;
    for (i = 0; i <= limit; i++)
    {
        for (j = 0; j <= limit; j++)
        {   
            //给三个孩子分配
            childern[0] = i;
            childern[1] = j;
            childern[2] = n - i - j;
            //前两个孩子肯定是满足的，因为有循环限制
            if(childern[2] <= limit && childern[2] >= 0)
            {
                // printf("%d %d %d \n",childern[0],childern[1],childern[2]);
                ans++;
            }

        }
    }
    return ans;
}

16.找出峰值

• 第一位和最后一位不可以，所以遍历直接不用遍历这俩就好了
• 然后去判断当前的数据是否严格大于前一位和后一位即可。

/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
int* findPeaks(int* mountain, int mountainSize, int* returnSize)
{
    int* ans = (int*)malloc(sizeof(int) * (mountainSize / 2));
    int size = 0,i;
    for (i = 1; i < mountainSize - 1; i++)
    {
        if(mountain[i] > mountain[i-1] && mountain[i] > mountain[i+1])
        {
            ans[size++] = i;
        }
    }

    *returnSize = size;
    return ans;
}

17.统计移除递增子数组的数目|

• 枚举所有的可能，暴力无限循环！！

bool IsIncreas(int* nums,int numsSize)
{
    for (int i = 0; i < numsSize - 1; i++)
    {
        if(nums[i] >= nums[i + 1])
        {
            return false;
        }
    }

    return true;
}


int incremovableSubarrayCount(int* nums, int numsSize)
{
    int i,j,ans = 0;
    for (i = 0; i < numsSize; i++)
    {
        for (j = i; j < numsSize; j++)
        {
            int* tmp = (int*)malloc(sizeof(int) * numsSize);
            int index = 0;
            int k;
            //左边
            for (k = 0; k < i; k++)
            {
                tmp[index++] = nums[k];
            }
            //右边
            for (k = j + 1; k < numsSize; k++)
            {
                tmp[index++] = nums[k];
            }
            //判断是否递增
            if(IsIncreas(tmp,index))
            {
                ans++;
            }
        }
    }

    return ans;
}   

18.文件组合

• 用暴力+枚举肯定是能做出来的，但是我想到暴力的时候，就又想到了双指针可以优化时间。

• 就是嗯。。。。。以前肯定做过类似的求和的题，当时就是用双指针来做的。

• 先模拟出一个数组来
  

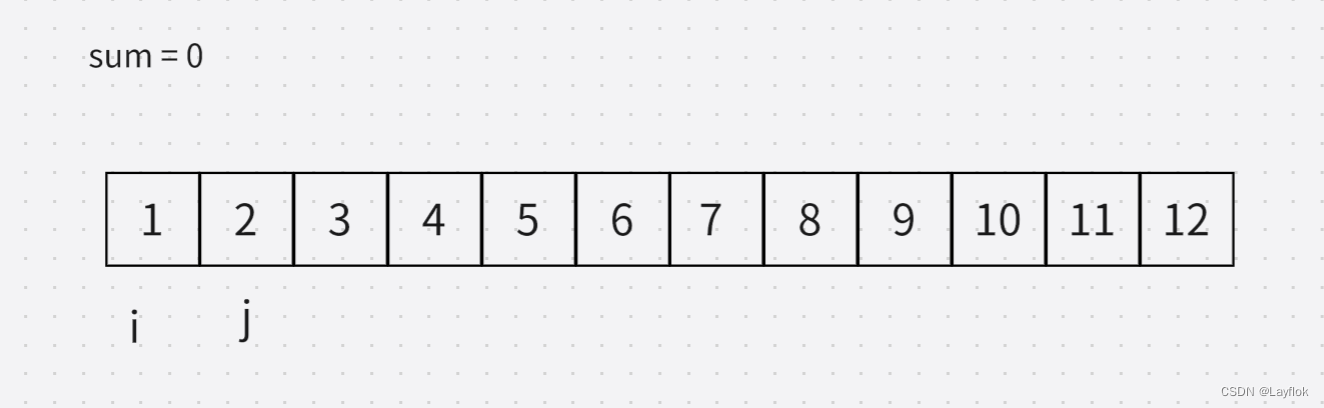
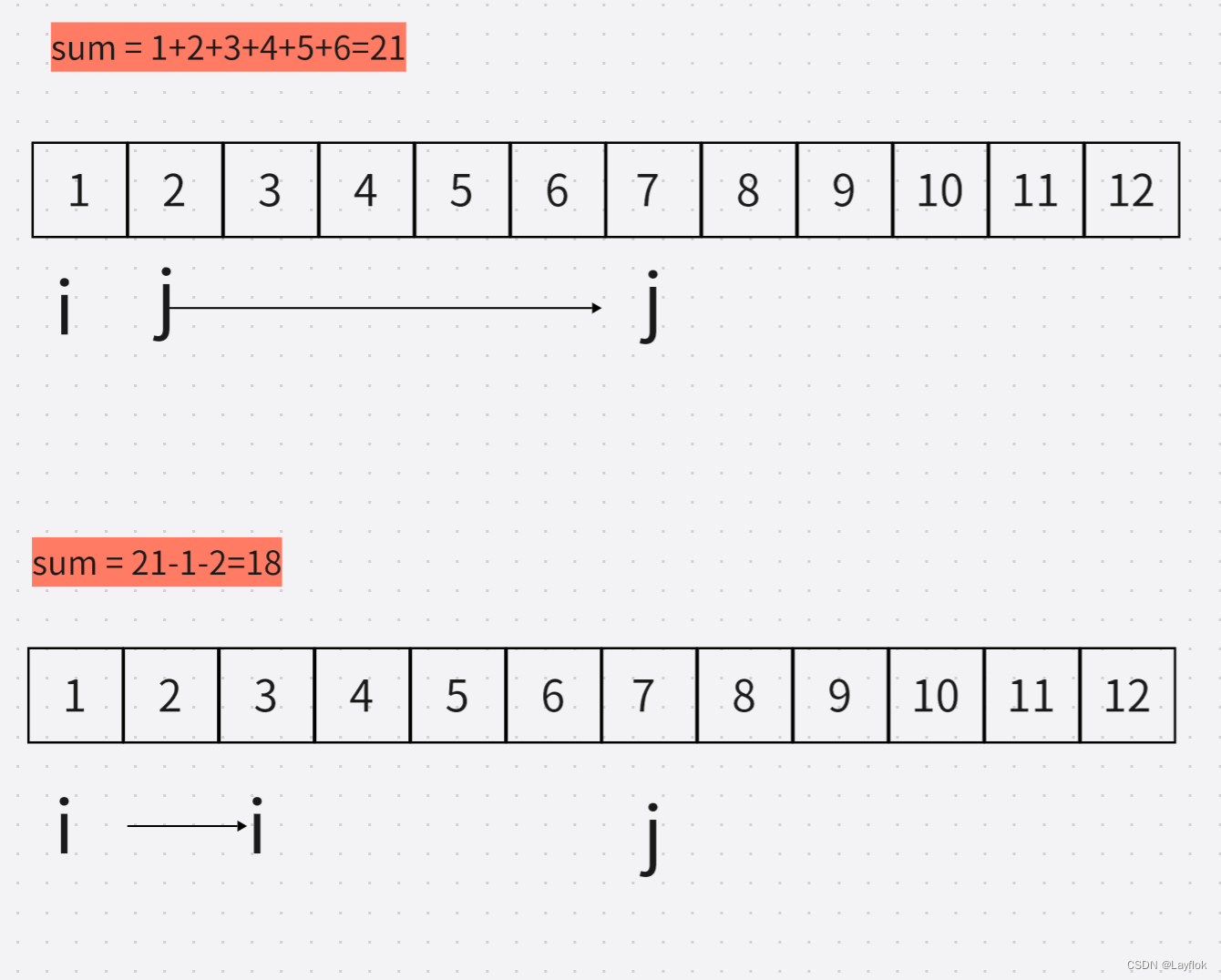
• 然后将第一个值赋给sum，然后去判断当前的sum 如果小于target的话，j++,

• 如果当前的sum 大于 target的话 i++;

• 这两者有区别的是，i++的时候是从sum中减去当前的值，j++是从sum中加上当前的值

• 如果两者相等的话，也找到了这一组数据，拷贝过去即可。
  

int** fileCombination(int target, int* returnSize, int** returnColumnSizes)
{
    //构造一个数组出来
    int* nums = (int*)malloc(sizeof(int) * target);
    int i,j;
    for (i = 0; i < target; i++)
    {
        nums[i] = i + 1;
    }
    int** ans = (int**)malloc(sizeof(int*) * (target / 2));
    *returnColumnSizes = (int*)malloc(sizeof(int) * (target / 2));
    int size = 0,sum = 0;
    i = 0,j = i + 1;
    sum += nums[i];
    while(i < target / 2)
    {
        
        if(sum < target)
        {
            sum += nums[j];
            j++;
        }
        else if(sum > target)
        {
            sum -= nums[i];
            i++;
        }
        else
        {
            ans[size] = (int*)malloc(sizeof(int) * j - i );
            memcpy(ans[size],nums+i,sizeof(int) * j - i );
            (*returnColumnSizes)[size++] = j - i;
            sum -= nums[i];
            i++;
        }
    }
    *returnSize = size;
    return ans;
}