leetcode 238. 除自身以外数组的乘积(优质解法)

代码:
class Solution {
public int[] productExceptSelf(int[] nums) {
int length =nums.length;
int[] f=new int[length]; //前缀积数组
int[] g=new int[length]; //后缀积数组
f[0]=g[length-1]=1; // 去除边界值
//填充前缀和后缀积数组
for(int i=1;i<length;i++){
f[i]=f[i-1]*nums[i-1];
}
for(int i=length-2;i>=0;i--){
g[i]=g[i+1]*nums[i+1];
}
int[]results=new int[length];
for(int i=0;i<length;i++){
results[i]=f[i]*g[i];
}
return results;
}
}
题解:
? ? ? ? 本题的题意描述得很清晰,我们要计算?nums 数组中每个下标除自身以外数组的乘积,对于 nums=【1,2,3,4】,result[ 1 ] = 1*3*4 = 12,
? ? ? ? 我们可以很简单的想到一个暴力解法,就是和题意一样,直接计算每个下标除自身以外数组的乘积,那么我们每计算一个下标对应的值就需要遍历一次数组,要计算 n 个下标,所以需要遍历 n 次,时间复杂度就为:O(n^2),这是很大的复杂度,我们需要进行优化
? ? ? ? 由于计算某个下标除自身以外数组的乘积,需要把下标之前和之后的数据都乘起来,我们可以先单独计算下标之前的数据乘积,再计算下标之后的数据乘积,再将得到的两个数据相乘,也能达到对应的效果,所以我们这里的解题可以用到前缀和的思想
? ? ? ? 为了方便理解,我画了如下的图:
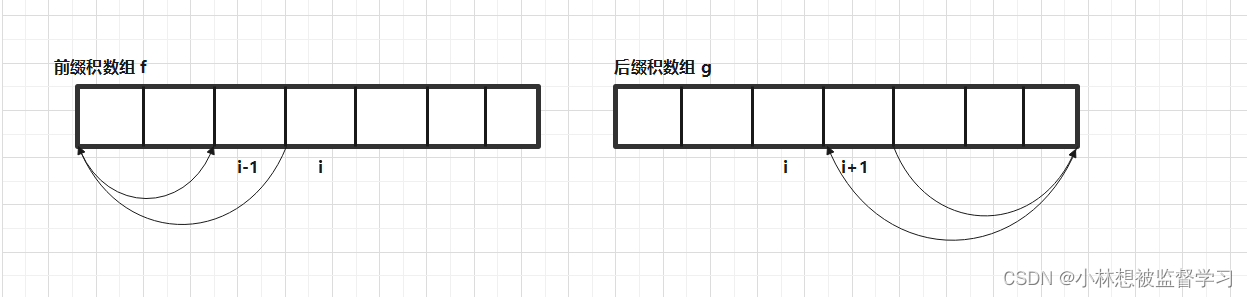
? ? ? ? 如上图,要想获得 f[ i ],即 i 下标的前缀积,可以先获得 i - 1 下标的前缀积,再乘以 nums[ i -1] ,我们得到推导式:f[ i ] = f[ i-1 ] * nums[ i-1 ]
? ? ? ? 要想获得 g[ i ],即 i 下标的后缀积,可以先获得 i + 1 下标的后缀积,再乘以 nums[ i +1] ,我们得到推导式:g[ i ] = g[ i+1 ] * nums[ i+1 ]
? ? ? ? 根据上面的推导式填充前缀积数组 f 和后缀积数组 g 即可,填充完以后,i 下标的结果 result[ i ] = f [ i ] * g[ i ]?
? ? ? ? 但其中有一个细节需要注意,在填充数组 f 时,当 i =0 ,会出现 -1 这个越界下标,所以我们需要提前初始化,当下标为 0 时,前缀积为 1,同理,在填充数组 g 时,当 i =nums.length -1??,会出现 nums.length 这个越界下标,所以我们需要提前初始化,当下标为 nums.length?时,后缀积为 1
????????
????????
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 助力工业焊缝质量检测,YOLOv3开发构建工业焊接场景下钢材管道焊缝质量检测识别分析系统
- Shell编程学习笔记04
- 金三银四-JAVA核心知识高频面试题
- 《PCI Express体系结构导读》随记 —— 第I篇 第2章 PCI总线的桥与配置(18)
- Halcon提取彩色多通道图像的亚像素边缘edges_color_sub_pix算子
- 从零学Java 线程的状态
- C语言关键字中英翻译机(用文件实现),有进阶(扩展了一个小游戏超有趣)
- 【c++】string类的模拟实现
- SpringBoot 配置文件
- python相关工具代码之网络图片下载并显示出下载图片保存到的地址