随机游走Python中的实现
发布时间:2023年12月17日
随机游走是一个数学对象,称为随机或随机过程,它描述了一条路径,该路径由一些数学空间(如整数)上的一系列随机步骤组成。随机游走的一个基本例子是整数线上的随机游走,它从0开始,每一步以相等的概率移动+1或-1。其他例子包括分子在液体或气体中行进时的路径,觅食动物的搜索路径,波动股票的价格和赌徒的财务状况都可以通过随机行走模型来近似,即使它们在现实中可能不是真正的随机。
如这些例子所示,随机游走在许多科学领域都有应用,包括生态学、心理学、计算机科学、物理学、化学、生物学以及经济学。随机游走解释了在这些领域中观察到的许多过程的行为,因此可以作为记录随机活动的基本模型。作为更数学的应用,pi的值可以通过在基于代理的建模环境中使用随机游走来近似。
别再说无聊的理论了。让我们休息一下,同时了解一些代码知识。所以,为了编码随机游走,我们基本上需要一些Python库,一些用来做数学,另一些用来绘制曲线。
所需库
- random
- numpy
- matplotlib
一维随机游走
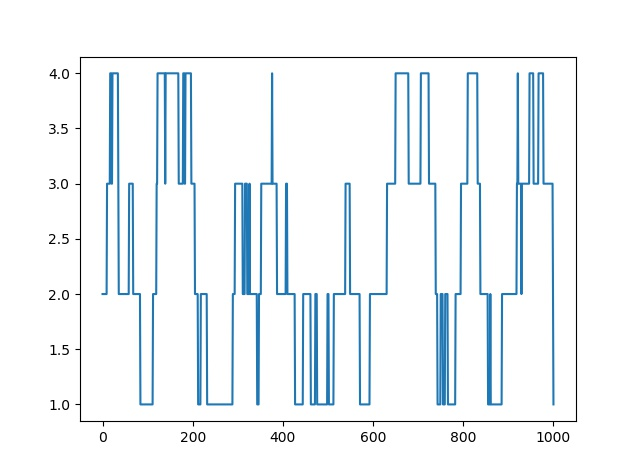
一维随机游走的一个基本例子是整数线上的随机游动,它从0开始,每一步移动+1或-1、概率相等。
# Python code for 1-D random walk.
import random
import numpy as np
import matplotlib.pyplot as plt
# Probability to move up or down
prob = [0.05, 0.95]
# statically defining the starting position
start = 2
positions = [start]
# creating the random points
rr = np.random.random(1000)
downp = rr < prob[0]
upp = rr > prob[1]
for idownp, iupp in zip(downp, upp):
down = idownp and positions[-1] > 1
up = iupp and positions[-1] < 4
positions.append(positions[-1] - down + up)
# plotting down the graph of the random walk in 1D
plt.plot(positions)
plt.show()
输出
二维随机游走
在高维数中,随机游走点的集合具有有趣的几何性质。事实上,人们得到了一个离散的分形,即在大尺度上表现出随机自相似性的集合。在小尺度上,可以观察到由执行行走的网格产生的“锯齿状”。随机游走的轨迹是所访问的点的集合,被认为是一个集合,而不考虑游走何时到达该点。在一个维度中,轨迹只是行走所达到的最小高度和最大高度之间的所有点。
# Python code for 2D random walk.
import numpy
import pylab
import random
# defining the number of steps
n = 100000
#creating two array for containing x and y coordinate
#of size equals to the number of size and filled up with 0's
x = numpy.zeros(n)
y = numpy.zeros(n)
# filling the coordinates with random variables
for i in range(1, n):
val = random.randint(1, 4)
if val == 1:
x[i] = x[i - 1] + 1
y[i] = y[i - 1]
elif val == 2:
x[i] = x[i - 1] - 1
y[i] = y[i - 1]
elif val == 3:
x[i] = x[i - 1]
y[i] = y[i - 1] + 1
else:
x[i] = x[i - 1]
y[i] = y[i - 1] - 1
# plotting stuff:
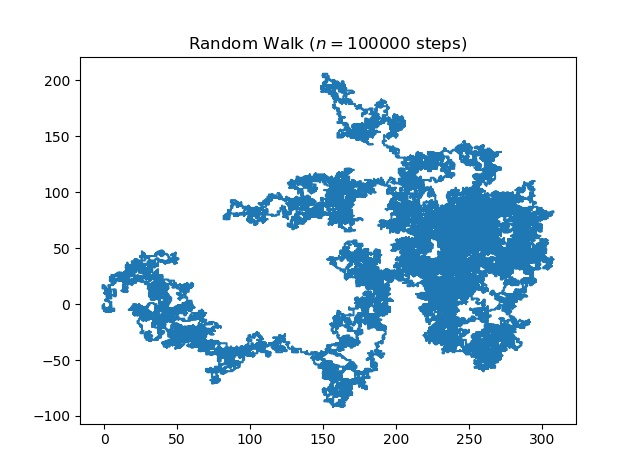
pylab.title("Random Walk ($n = " + str(n) + "$ steps)")
pylab.plot(x, y)
pylab.savefig("rand_walk"+str(n)+".png",bbox_inches="tight",dpi=600)
pylab.show()
输出
应用领域
- 在计算机网络中,随机游走可以对在服务器处缓冲的传输分组的数量进行建模。
- 在群体遗传学中,随机游走描述了遗传漂变的统计特性。
- 在图像分割中,随机游走被用于确定标签(即,“对象”或“背景”)以与每个像素相关联。
- 在大脑研究中,随机游走和强化随机游走被用来模拟大脑中神经元放电的级联。
- 随机游走也被用于对诸如在线社交网络之类的大规模在线图进行采样。
文章来源:https://blog.csdn.net/qq_42034590/article/details/132536702
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- Spring Bean 线程安全吗?
- idea个人常用快捷键汇总
- 车载导航系统UI界面,可视化大屏设计(PS源文件)
- 【MATLAB】CEEMD+FFT+HHT组合算法
- 处理器中异常的处理
- 【Java】——期末复习题库(十一)
- vue+element实现动态表格:根据后台返回的属性名和字段动态生成可变表格
- Python源码35:海龟画图turtle画中国结
- Certum与Geotrust的SSL证书区别
- Salesforce推出Trailblazer就业市场,让求职更简单!