HDU - 2063 过山车（Java & JS & Python & C）

题目来源

Problem - 2063 (hdu.edu.cn)

题目描述

RPG girls今天和大家一起去游乐场玩，终于可以坐上梦寐以求的过山车了。

可是，过山车的每一排只有两个座位，而且还有条不成文的规矩，就是每个女生必须找个男生做partner和她同坐。

但是，每个女孩都有各自的想法，举个例子把，

• Rabbit只愿意和XHD或PQK做partner
• Grass只愿意和linle或LL做partner
• PrincessSnow愿意和水域浪子或伪酷儿做partner

考虑到经费问题，boss刘决定只让找到partner的人去坐过山车，其他的人，嘿嘿，就站在下面看着吧。

聪明的Acmer，你可以帮忙算算最多有多少对组合可以坐上过山车吗？

输入描述

输入数据的第一行是三个整数K , M , N，分别表示可能的组合数目，女生的人数，男生的人数。

• 0 < K ≤?1000
• 1?≤?N, M ≤ 500

接下来的K行，每行有两个数，分别表示女生 Ai 愿意和男生 Bj 做partner。

最后一个0结束输入。

输出描述

对于每组数据，输出一个整数，表示可以坐上过山车的最多组合数。

用例

输入	6 3 3 1 1 1 2 1 3 2 1 2 3 3 1 0
输出	3

题目解析

本题是二分图最大匹配问题。

首先，我们需要知道什么是二分图？

二分图是一种特殊的图结构，二分图中的节点可以分为两部分，每个部分中的节点之间互不相连，比如下图所示：

绿色点集是一个部分，橙色点集是一个部分，各个部分中节点之间互不相连

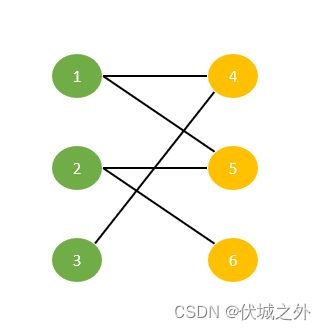
二分图的 "匹配" 指的是 "边的集合“，"匹配"中的各个边之间没有共同节点，即每个边都是独立的。

比如下图中的两个红色边就形成了一个匹配，因为1-4边，2-5边之间没有共同节点，两个边是互相独立的。

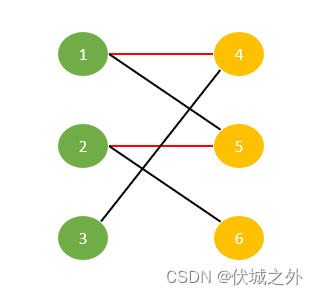
二分图的最大匹配，指的是，边最多的"匹配"，比如下图中，1-5边，2-6边，3-4边之间互相独立，可以形成一个数量为3条边的匹配。下面二分图最多只能有3条边的匹配。

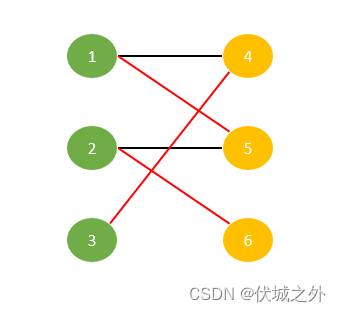
那么，如何求二分图的最大匹配呢？

最常用的办法就是匈牙利算法。

在解释匈牙利算法之前，我们需要先对二分图最大匹配问题的实际意义做一个解释。

比如现在有男生若干，女生若干，而每个男生都有心仪的多个女生，每个女生也有心仪的多个男生，而男生、女生只会和心仪的对象进行配对，现在需要实现最大配对？

上面例子就是二分图最大匹配的典型应用。

我们假设节点1，2，3是男生，4，5，6是女生，那么初始时，存在如下心仪关系：

• 1 和 4 互相心仪
• 1 和?5 互相心仪
• 2 和?5 互相心仪
• 2?和 6?互相心仪
• 3 和 4?互相心仪

因此可得二分图如下：

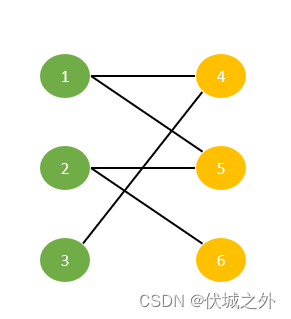
下面开始演示匈牙利算法来找到最大匹配数：

我们需要选择二分图的一部分作为发起配对请求的一方，比如我们选择男生作为发起配对请求的一方，此时遍历每一个男生：

假设先遍历出男生1，而男生1和与女生4，女生5互相心仪，此时我们可以任选一个女生进行配对，比如选择女生4进行配对，由于女生4当前没有配对对象，因此男生1和女生4可以配对成功

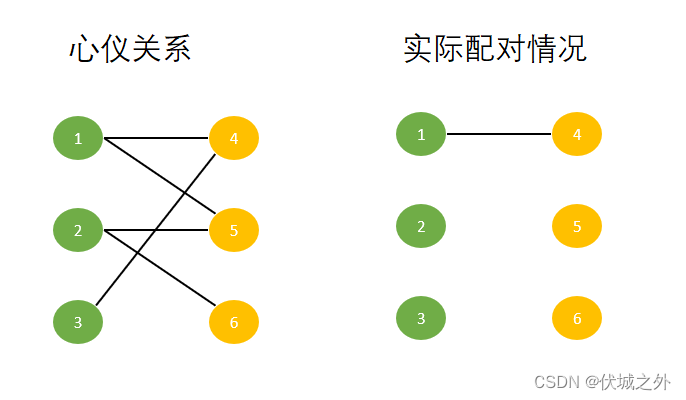
男生1完成配对后，继续遍历下一个男生2发起配对请求，而男生2和女生5，女生6互相心仪，此时我们可以任选一个女生进行配对，比如选择女生5进行配对，由于女生5当前没有配对对象，因此男生2和女生5可以配对成功

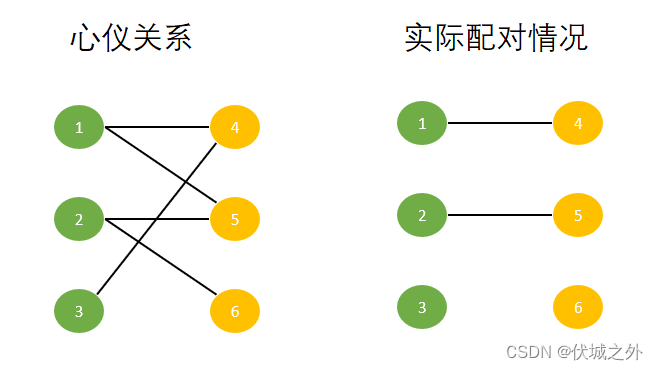
男生2完成配对后，继续遍历下一个男生3发起配对请求，而男生3只和女生4互相心仪，但是女生4已经和男生1配对了！！！

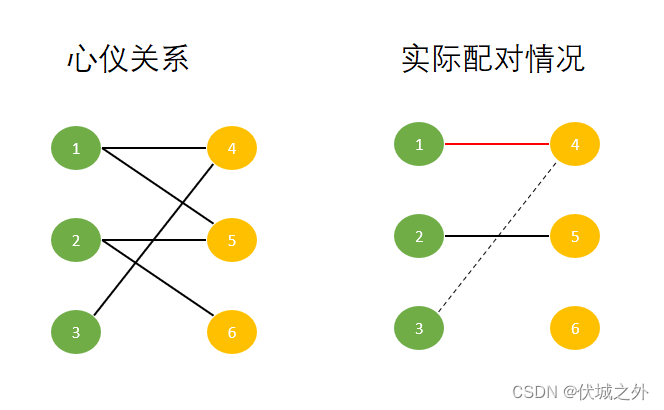
此时，为了实现最大配对，我们只能委屈男生1，让他找一找其他可以配对的女生，然后发现男生1还和女生5互相心仪，因此我们尝试将男生1和女生5配对。

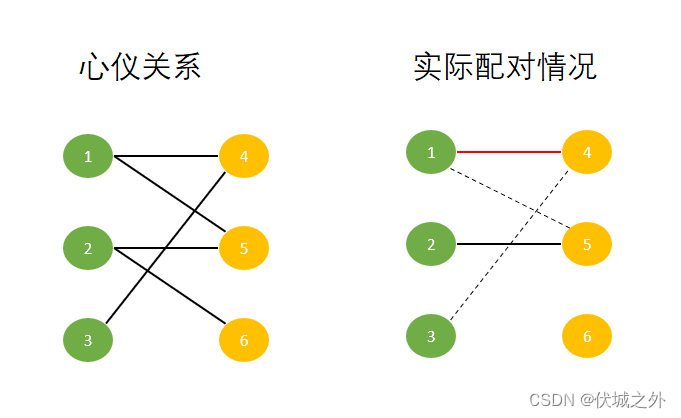
但是女生5已经和男生2发生配对了！！！

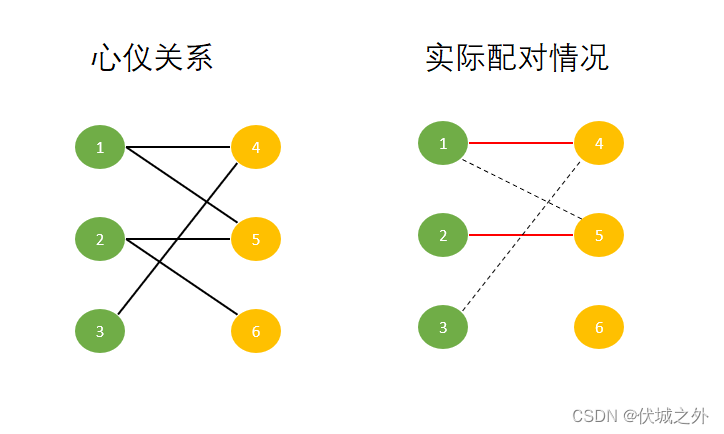
因此，为了实现最大配对，只能委屈男生2找找看其他可以配对的女生，然后发现男生2还和女生6互相心仪，因此尝试将那是2和女生6进行配对

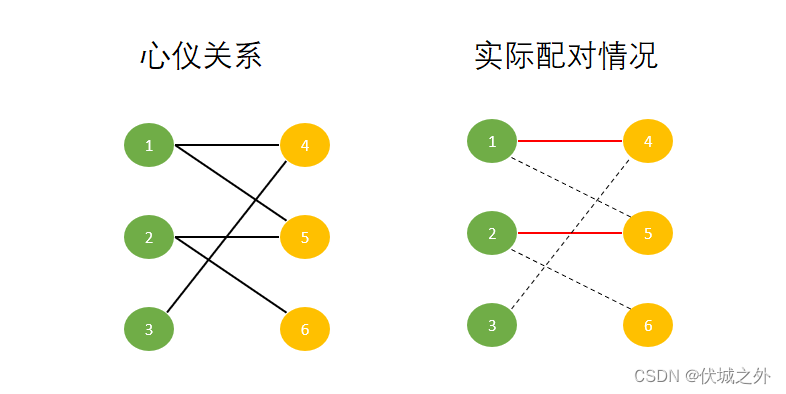
而女生6没有发生过配对，因此男生2可以和女生6成功配对。

由于男生2和女生6成功配对了，因此虚线2-6变为实线，而一个男生只能和一个女生配对，因此实线2-5变为虚线

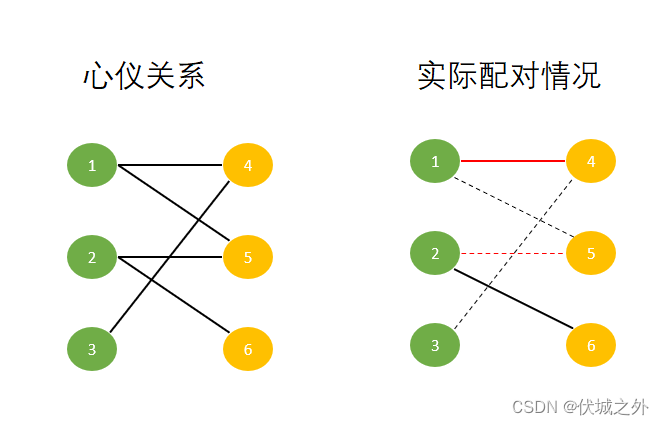
而由于女生5和男生2解除了配对状态，因此男生1和女生5就可以成功配对，因此1-5从虚线变为实线，而一个男生只能和一个女生配对，因此实线1-4变为虚线

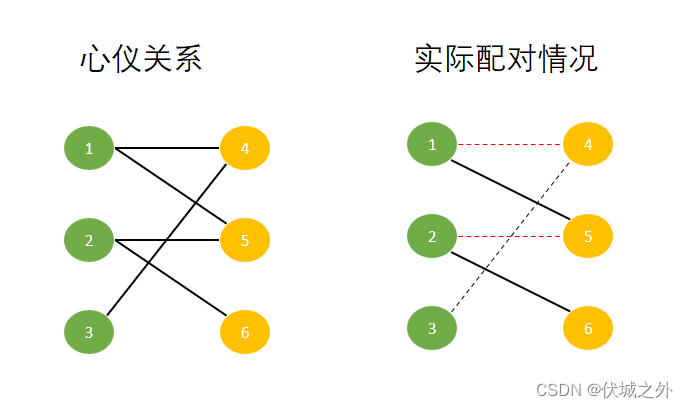
由于女生4和男生1解除了配对状态，因此男生3和女生4可以成功配对，因此虚线3-4变为实线

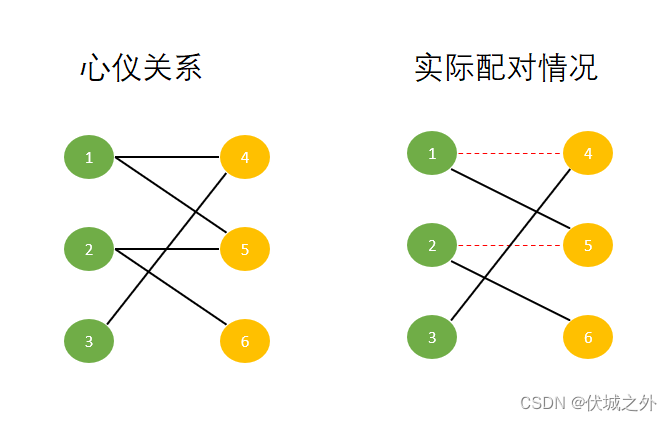
此时我们完成了所有男生的配对，即得到了最大匹配。

上面，从配对情况图中，黑虚线和红实线，逆变为，黑实线和红虚线，实现了配对数+1，

如下图左边只有两个配对（红色线），右边有三个配对（黑色线）

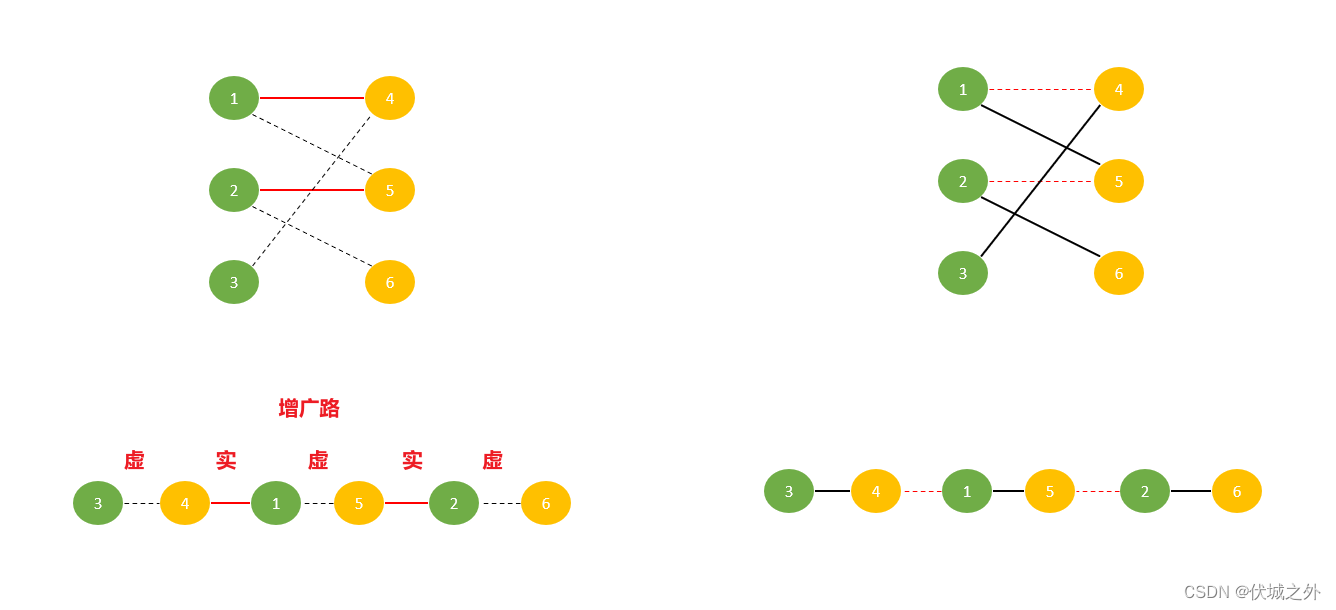
我们将左边这种展开为“虚实虚实虚”的情况，称为增广路，增广路的特点是两端为虚，中间虚实交替，增广路的逆变，可以实现配对数+1。

关于增广路的定义和意义就是如此，了解即可。

以上就是匈牙利算法的实现过程。总结一下就是：

初始时，寻找一方作为配对发起方，比如男生，遍历每一个男生发起配对请求：

男生a只能对互相心仪的女生发起配对请求，

• 如果互相心仪的女生b没有发生过配对，则和当前男生配对成功
• 如果互相心仪的女生b已经发生了配对，那么需要找到女生b的配对对象男生c，并尝试让男生c重新找一个可以配对的其他女生（此时为递归重复逻辑，即男生c对其他互相心仪的女生发起配对请求），如果最终男生c可以配对其他女生，则男生a与女生b配对成功，否则男生a与女生b无法配对。

按照上面逻辑我们让每一个男生都发起配对请求，最终我们可以找到最大匹配数。

更多细节请看下面代码实现。

Java算法源码

import java.util.Arrays;
import java.util.Scanner;

public class Main {
  static int m;
  static int n;
  static boolean[][] edges;
  static int[] match;
  static boolean[] vis;

  public static void main(String[] args) {
    Scanner sc = new Scanner(System.in);

    while (sc.hasNextInt()) {
      int k = sc.nextInt();

      if (k == 0) break;

      m = sc.nextInt(); // m个女生
      n = sc.nextInt(); // n个男生

      // edges[a][b] == true 表示 a女生 和 b男生 可以配对
      edges = new boolean[m + 1][n + 1];
      for (int i = 0; i < k; i++) {
        int a = sc.nextInt();
        int b = sc.nextInt();
        edges[a][b] = true;
      }

      // match[b] 表示男生b配对的女生
      match = new int[n + 1];
      // vis[b] 表示男生b是否在本次增广路中
      vis = new boolean[n + 1];

      // ans记录题解
      int ans = 0;

      // 遍历女生a
      for (int a = 1; a <= m; a++) {
        // 从女生a开始进行增广路探索，探索前，需要将vis重置
        Arrays.fill(vis, false);
        // 如果a找到配对男生，则配对边+1
        if (dfs(a)) ans++;
      }

      System.out.println(ans);
    }
  }

  public static boolean dfs(int a) {
    // 遍历男生b
    for (int b = 1; b <= n; b++) {
      // 如果男生b不在女生a发起的探索的增广路中，且a,b可以配对
      if (!vis[b] && edges[a][b]) {
        // 则当前增广路加入男生b
        vis[b] = true;

        // 如果男生b没有被其他人配对 || 已经和其他人配对，但是男生b当前配对的女生match[b]可以放弃男生b，而和其他男生配对
        if (match[b] == 0 || dfs(match[b])) {
          // 则男生b可以和女生a配对，即配对成功，match[b] = a
          match[b] = a;
          return true;
        }
      }
    }

    return false;
  }
}

?

JS算法源码

const rl = require("readline").createInterface({ input: process.stdin });
var iter = rl[Symbol.asyncIterator]();
const readline = async () => (await iter.next()).value;

void (async function () {
  // m个女生, n个男生, k条边
  const [k, m, n] = (await readline()).split(" ").map(Number);

  // edges[a][b] == true 表示 a女生 和 b男生 可以配对
  const edges = new Array(m + 1)
    .fill(0)
    .map(() => new Array(n + 1).fill(false));

  for (let i = 0; i < k; i++) {
    const [a, b] = (await readline()).split(" ").map(Number);
    edges[a][b] = true;
  }

  await readline(); // 读取最后一行输入的0

  // match[b] 表示男生b配对的女生
  const match = new Array(n + 1).fill(0);
  // vis[b] 表示男生b是否在本次增广路中
  const vis = new Array(n + 1).fill(false);

  // ans记录题解
  let ans = 0;

  // 遍历女生a
  for (let a = 1; a <= m; a++) {
    // 从女生a开始进行增广路探索，探索前，需要将vis重置
    vis.fill(false);
    // 如果a找到配对男生，则配对边+1
    if (dfs(a)) ans++;
  }

  function dfs(a) {
    // 遍历男生b
    for (let b = 1; b <= n; b++) {
      // 如果男生b不在女生a发起的探索的增广路中，且a,b可以配对
      if (!vis[b] && edges[a][b]) {
        // 则当前增广路加入男生b
        vis[b] = true;

        // 如果男生b没有被其他人配对 || 已经和其他人配对，但是男生b当前配对的女生match[b]可以放弃男生b，而和其他男生配对
        if (match[b] == 0 || dfs(match[b])) {
          // 则男生b可以和女生a配对，即配对成功，match[b] = a
          match[b] = a;
          return true;
        }
      }
    }

    return false;
  }

  console.log(ans);
})();

?

Python算法源码

# 输入获取
k, m, n = map(int, input().split())  # k个配对, m个女生, n个男生

edges = [[False] * (n + 1) for _ in range(m + 1)]
for _ in range(k):
    a, b = map(int, input().split())
    edges[a][b] = True  # edges[a][b] == true 表示 a女生 和 b男生 可以配对

input()

match = [0] * (n + 1)  # match[b] 表示男生b确定配对的女生


def dfs(a, vis):
    #  遍历男生b
    for b in range(1, n + 1):
        # 如果男生b不在女生a发起的探索的增广路中，且a,b可以配对
        if not vis[b] and edges[a][b]:
            # 则当前增广路加入男生b
            vis[b] = True

            # 如果男生b没有被其他人配对 || 已经和其他人配对，但是男生b当前配对的女生match[b]可以放弃男生b，而和其他男生配对
            if match[b] == 0 or dfs(match[b], vis):
                # 则男生b可以和女生a配对，即配对成功，match[b] = a
                match[b] = a
                return True

    return False


# 算法入口
def getResult():
    ans = 0

    for a in range(1, m + 1):
        # vis[b] 表示男生b是否在a女生发起的增广路探索中
        vis = [False] * (n + 1)

        # 如果a找到配对男生，则配对边+1
        if dfs(a, vis):
            ans += 1

    return ans


# 算法调用
print(getResult())

C算法源码

#include <stdio.h>

#define MAX_SIZE 501

#define TRUE 1
#define FALSE 0

int m, n; // m个女生, n个男生
int edges[MAX_SIZE][MAX_SIZE]; // edges[a][b] == true 表示 a女生 和 b男生 可以配对
int match[MAX_SIZE]; // match[b] 表示男生b配对的女生
int vis[MAX_SIZE]; // vis[b] 表示男生b是否在本次增广路中

int dfs(int a) {
    // 遍历男生b
    for (int b = 1; b <= n; b++) {
        // 如果男生b不在女生a发起的探索的增广路中，且a,b可以配对
        if (!vis[b] && edges[a][b]) {
            // 则当前增广路加入男生b
            vis[b] = 1;

            // 如果男生b没有被其他人配对 || 已经和其他人配对，但是男生b当前配对的女生match[b]可以放弃男生b，而和其他男生配对
            if (match[b] == 0 || dfs(match[b])) {
                // 则男生b可以和女生a配对，即配对成功，match[b] = a
                match[b] = a;
                return TRUE;
            }
        }
    }

    return FALSE;
}

int main() {
    while (1) {
        int k;
        scanf("%d", &k);

        if (k == 0) break;

        scanf("%d %d", &m, &n);

        // 初始化edges
        for (int i = 0; i <= m; i++) {
            for (int j = 0; j <= n; j++) {
                edges[i][j] = FALSE;
            }
        }

        // 关联可匹配的男女生
        for (int i = 0; i < k; i++) {
            int a, b;
            scanf("%d %d", &a, &b);
            edges[a][b] = TRUE;
        }

        // 初始化match
        for (int i = 0; i <= n; i++) {
            match[i] = 0;
        }

        // ans记录题解
        int ans = 0;
        // 遍历女生
        for (int a = 1; a <= m; a++) {
            // 初始化vis
            for (int i = 0; i <= n; i++) {
                vis[i] = FALSE;
            }

            // 如果女生a找到匹配男生，则匹配边++
            if (dfs(a)) {
                ans++;
            }
        }

        printf("%d\n", ans);
    }

    return 0;
}