2.1.2 一个关于y=ax+b的故事

跳转到根目录：知行合一：投资篇

已完成：
1、投资&技术
??1.1.1 投资-编程基础-numpy
??1.1.2 投资-编程基础-pandas
??1.2 金融数据处理
??1.3 金融数据可视化
2、投资方法论
??2.1.1 预期年化收益率
??2.1.2 一个关于y=ax+b的故事
3、投资实证
??[3.1 2023这一年] 被鸽

当看到一个在k线图上画直线的时候，斜率是可以自动计算的吗？

最佳拟合的直线，计算出来的斜率是多少？最佳拟合直线代表的年化是多少？

1. 系统自己画！最佳拟合线

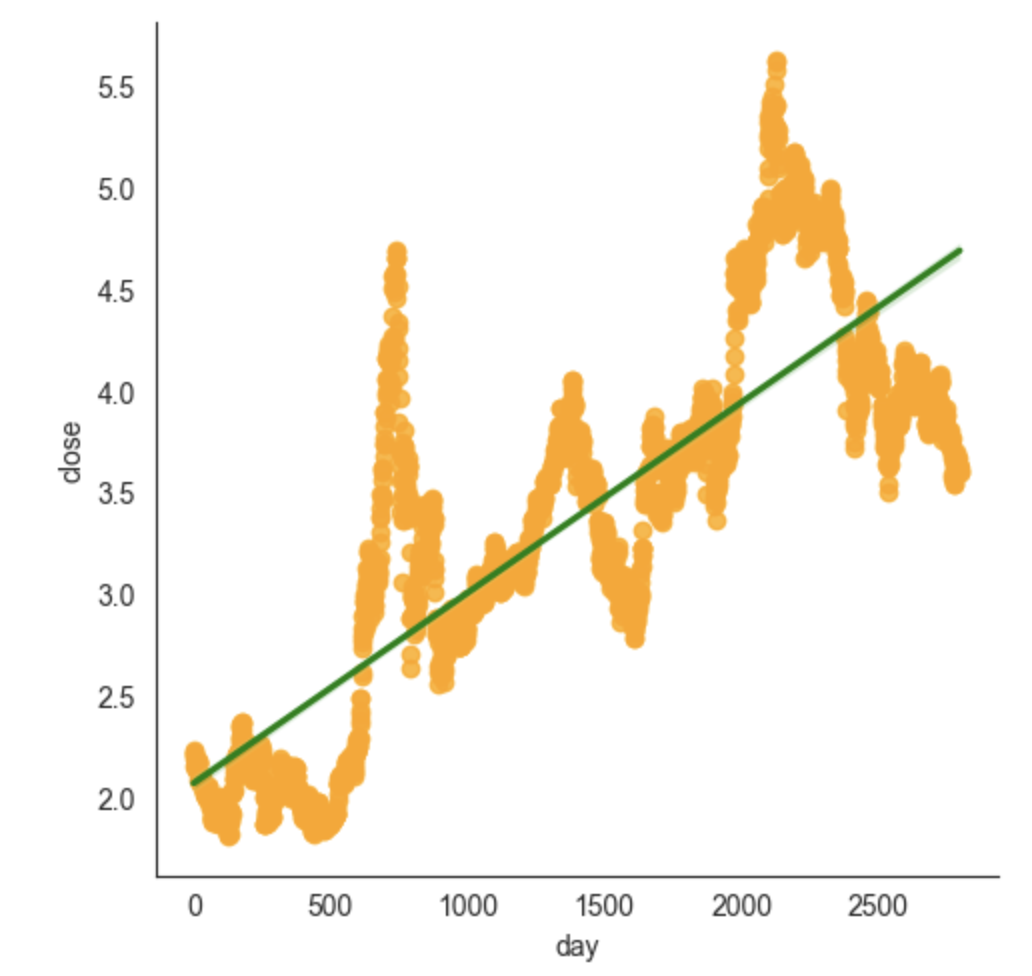
1.1. 沪深300的最佳拟合线

顾名思义，这就是对于散点图，画一条最佳拟合的直线。那什么又叫最佳拟合线？

最佳拟合直线是指，我们可以找到一条直线，样本点到该直线的[离差平方和]达到最小的直线。这条直线用公式y = ax + b表示。

a表示回归系数，b表示截距。

再简单的说，就是存在一条线，这条线，能让各个点，都比较“满意”地分布在其上下。

我们拿沪深300的历史收盘价作为散点图，来看看其所谓的最佳拟合线是什么样的。

import qstock as qs
import seaborn as sns
import numpy as np

sh300=qs.get_data('510300')
# 因为设想中，x轴，可以是一个顺序的数组，比如从0开始往后数，step为1。这其实就是暗合着，随着时间的增加，close是否能拟合一条向上的直线？
sh300['day'] = np.arange(0, sh300.shape[0], 1)

sns.set_style("white")
gridobj = sns.lmplot(x="day", y="close", data=sh300, 
                     ci=95, scatter_kws={'color': 'orange'}, line_kws={'color': 'green'}, markers='o')

1.2. 横向对比：一个个算

看过了沪深300，肯定会有疑惑啊，总是要横向对比的吧？比如沪深300和中证500、券商ETF、红利ETF、房地产ETF、黄金ETF等标的，能进行横向对比来看谁的斜率(赚钱效应)更好吗？

Of course ,动手！

import qstock as qs
import seaborn as sns
import numpy as np

stocks_info = [
    {'code': '510300', 'name': '沪深300'},
    {'code': '510500', 'name': '中证500'},
    {'code': '512010', 'name': '医药ETF'},
    {'code': '512000', 'name': '券商ETF'},
    {'code': '516160', 'name': '新能源ETF'},
    {'code': '510800', 'name': '红利ETF'},
    {'code': '518880', 'name': '黄金ETF'},
    {'code': '512200', 'name': '房地产ETF'}
]
for stock in stocks_info:
    df=qs.get_data(stock['code'])
    # 因为设想中，x轴，可以是一个顺序的数组，比如从0开始往后数，step为1。这其实就是暗合着，随着时间的增加，close是否能拟合一条向上的直线？
    df['day'] = np.arange(0, df.shape[0], 1)
    df['标的'] = stock['name']

    sns.set_style("white")
    # 这个是seaborn中文乱码的处理。经过试验，在这里，plt.rcParams['font.sans-serif'] = ['Arial Unicode MS']，这种设置是不行的。
    sns.set_style(rc= {'font.sans-serif':"Arial Unicode MS"})
    gridobj = sns.lmplot(x="day", y="close", data=df,  hue="标的", 
                         ci=95, scatter_kws={'color': 'orange'}, line_kws={'color': 'green'}, markers='o')

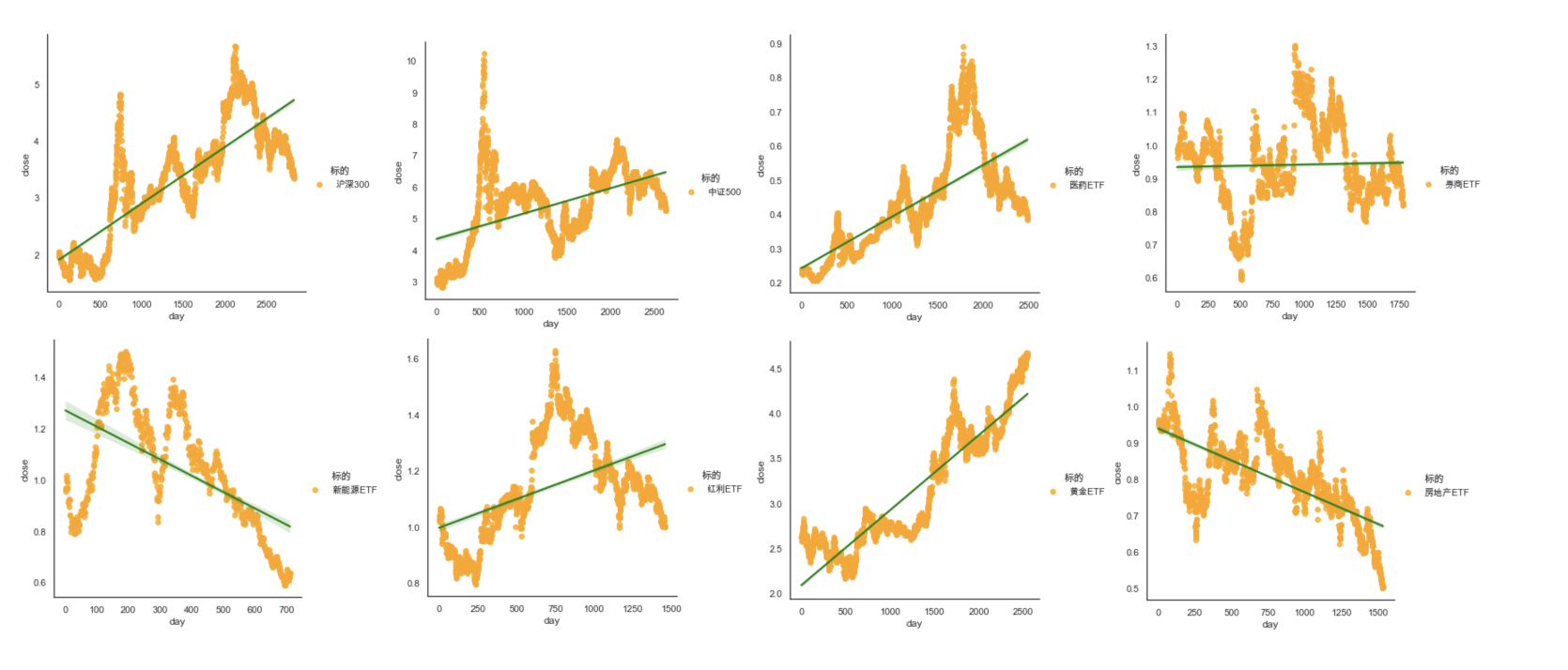
这里要说明一下，上面其实是一个个图生成的，然后我一张张图拼接起来的结果。

如果想直接横向着来看，还需要对数据进行标准化处理，如果不进行标准化，那比如不同标的的收盘价，差异很大，有的是十几块，像ETF，可能就是1块，那结果就很难看，就像下面这种：

1.3. 横向对比：数据标准化

所以，下面就是要将不同的标的进行标准化处理，这种标准化，意味着，将价格进行处理变成相对值，才可以进行比较，这里使用的是sklearn模块的StandardScaler，核心方法是fit_transform(df_all)。如果没有安装sklearn，需要先进行安装pip install -U scikit-learn

下面是一个完整的案例：

import qstock as qs
import pandas as pd

#默认日频率、前复权所有历史数据
#open：开盘价，high：最高价，low：最低价，close：收盘价 vol：成交量，turnover：成交金额，turnover_rate:换手率
# 沪深300， 中证500， 医药ETF, 券商ETF， 新能源ETF， 红利ETF, 黄金ETF, 房地产ETF
stocks_info = [
    {'code': '510300', 'name': '沪深300'},
    {'code': '510500', 'name': '中证500'},
    {'code': '512010', 'name': '医药ETF'},
    {'code': '512000', 'name': '券商ETF'},
    {'code': '516160', 'name': '新能源ETF'},
    {'code': '510800', 'name': '红利ETF'},
    {'code': '518880', 'name': '黄金ETF'},
    {'code': '512200', 'name': '房地产ETF'}
]
for stock in stocks_info:
    df = qs.get_data(stock['code'])  # 从qstock获取对应的股票历史数据
    stock['history_df'] = df         # 将其存在 history_df 这个key里面。

# 只保留收盘价，合并数据
df_all = pd.DataFrame()
for stock in stocks_info:
    df = stock['history_df']
    df = df[['close']]         # 只需要 date 和 close 2列就行了。
    df.rename(columns={'close': stock['name']}, inplace=True)  # 用股票的名字来重命名close列
    if df_all.size == 0:
        df_all = df
    else:
        df_all = df_all.join(df)  # join是按照index来连接的。

# print(df_all)

# 对dataframe的数据进行标准化处理
import sklearn
from sklearn import preprocessing
z_scaler = preprocessing.StandardScaler()   # 建立 StandardScaler 对象
z_data = z_scaler.fit_transform(df_all) #数据标准化（从第三列开始）
z_data = pd.DataFrame(z_data)                           #将数据转为Dataframe
z_data.columns = df_all.columns
df_all = z_data
print(df_all)


# 只保留收盘价，合并数据
df_new = pd.DataFrame()
for stock in stocks_info:
    df = df_all[[stock['name']]]
    df.columns = ['close']
    df['标的'] = stock['name']
    if df_new.size == 0:
        df_new = df
    else:
        df_new = pd.concat([df_new, df], axis=0)

print(df_new)
df_new['day'] = df_new.index

# 这个是seaborn中文乱码的处理。经过试验，在这里，plt.rcParams['font.sans-serif'] = ['Arial Unicode MS']，这种设置是不行的。
sns.set_style(rc= {'font.sans-serif':"Arial Unicode MS"})
df = sns.lmplot(x="day", y="close",data=df_new,col="标的")

         close      标的
0    -1.316309   沪深300
1    -1.275999   沪深300
2    -1.284061   沪深300
3    -1.290107   沪深300
4    -1.290107   沪深300
...        ...     ...
2826 -2.711143  房地产ETF
2827 -2.684416  房地产ETF
2828 -2.702234  房地产ETF
2829 -2.666598  房地产ETF
2830 -2.675507  房地产ETF

[22648 rows x 2 columns]

1.4. 看图说话

从上面的横向对比图可以看出：

1. 沪深300的斜率，是高于中证500的
2. 券商ETF，基本是一条横线，说明什么？做T啊，稳赚不赔！
3. 新能源ETF、房地产ETF，可能是时间还太短，所处的周期内，就是向下的。
4. 其他的，黄金看的是长周期，可能是几十年，还是慎重为好；红利，说不好，不懂的就先不碰了。

2. 系统自己算！线性回归

2.1. 沪深300线性回归，斜率0.00099414

首先从 sklearn 下的 linear_model 中引入 LinearRegression，再创建估计器起名 model，设置超参数 normalize 为 True，指的在每个特征值上做标准化，这样会加速数值运算。（可能是版本不同，有时候会报错LinearRegression got an unexpected keyword argument 'normalize'，此时反而要去掉normalize=True这个参数。）

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression

df=qs.get_data('510300')

model = LinearRegression()
model
x = np.arange(df.shape[0])
y = df['close']

X = x[:, np.newaxis]
model.fit( X, y )

print( model.coef_ )  # 斜率 0.00099414，就是y=ax+b的a
print( model.intercept_ )  # 截距 1.9，就是y=ax+b的b

# 根据上面计算的结果，我们绘制一个收盘价走势图和一条y=ax=b的直线
plt.plot( x, y,  linestyle='-', color='green' )
plt.plot(x, 0.00099414*x + 1.9, linestyle='--', color='r')  # 这个是根据最后计算的“斜率”和“截距”，再叠加绘制的斜线

2.2. 沪深300线性回归的年化，年化8.5%

之前计算的沪深300最佳拟合的直线，斜率和截距：

plt.plot(x, 0.00099414*x + 1.9, linestyle='--', color='r')  # 这个是根据最后计算的“斜率”和“截距”，再叠加绘制的斜线

沪深300，如果按照上面的直线来看，那：

起始点：1.9

终点：y=ax+b，即y=0.00099414*x + 1.9，最后的x，其实是x轴的个数，是：df.shape[0]，也就是行数：x=2832；那么计算的y = 0.00099414 * 2832 + 1.9 = 4.71540448

按照上面的计算：

import math

begin = 1.9
end = 4.71540448
year = 2832/255.0

# 年化收益率计算
rate = math.pow(end / begin, 1.0 / year) - 1
print('开始价=%s, 最终价=%s, year=%s，年化收益率=%s' % (str(begin), str(end), str(year), str(rate)))

开始价=1.9, 最终价=4.71540448, year=11.105882352941176，年化收益率=0.0852895190354479

2.3. 沪深300首尾点的年化，4.72%

如果不考虑中间的波动，那沪深300的年化收益率计算：

import pandas as pd
import math

df=qs.get_data('510300')

begin = df['close'][0]
end = df['close'][-1]
year = df.shape[0]/255.0

# 年化收益率计算
rate = math.pow(end / begin, 1.0 / year) - 1
print('开始价=%s, 最终价=%s, year=%s，年化收益率=%s' % (str(begin), str(end), str(year), str(rate)))

开始价=2.004, 最终价=3.345, year=11.105882352941176，年化收益率=0.047211214375309396

2.4. 中证500线性回归，斜率0.0008

对比看下中证500斜率如何

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression

df=qs.get_data('510500')

model = LinearRegression()
model
x = np.arange(df.shape[0])
y = df['close']

X = x[:, np.newaxis]
model.fit( X, y )

print( model.coef_ )  # 斜率 0.00080245，就是y=ax+b的a
print( model.intercept_ )  # 截距 4.353948387096773，就是y=ax+b的b

# 根据上面计算的结果，我们绘制一个收盘价走势图和一条y=ax=b的直线
plt.plot( x, y,  linestyle='-', color='green' )
plt.plot(x, 0.00080245*x + 4.353948387096773, linestyle='--', color='r')  # 这个是根据最后计算的“斜率”和“截距”，再叠加绘制的斜线

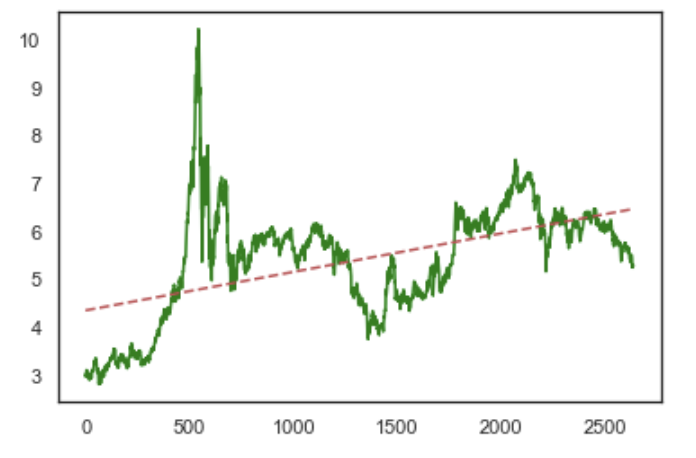
2.5. 中证500线性回归的年化

计算中证500最佳拟合的直线，斜率和截距：

plt.plot(x, 0.00080245*x + 4.353948387096773, linestyle='--', color='r')  # 这个是根据最后计算的“斜率”和“截距”，再叠加绘制的斜线

起始点：4.353948387096773

终点：y=ax+b，即y=0.00080245*x + 4.353948387096773，最后的x，其实是x轴的个数，是：df.shape[0]，也就是行数：x=2635；那么计算的y = 0.00080245 * 2635 + 4.353948387096773 = 6.468404137096773

按照上面的计算：

import math

begin = 4.353948387096773
end = 6.468404137096773
year = 2635/255.0

# 年化收益率计算
rate = math.pow(end / begin, 1.0 / year) - 1
print('开始价=%s, 最终价=%s, year=%s，年化收益率=%s' % (str(begin), str(end), str(year), str(rate)))

开始价=4.353948387096773, 最终价=6.468404137096773, year=10.333333333333334，年化收益率=0.039050907738202856

2.6. 中证500首尾点的年化

中证500年化收益率：

import pandas as pd
import math

df=qs.get_data('510500')

begin = df['close'][0]
end = df['close'][-1]
year = df.shape[0]/255.0

# 年化收益率计算
rate = math.pow(end / begin, 1.0 / year) - 1
print('开始价=%s, 最终价=%s, year=%s，年化收益率=%s' % (str(begin), str(end), str(year), str(rate)))

开始价=3.021, 最终价=5.279, year=10.333333333333334，年化收益率=0.055499799550948525

3. 总结

如果用最佳拟合直线，那么沪深300的年化是8.5%，中证500的年化是3.9%

如果是按照收盘价的首尾点来计算，那么沪深300的年化是4.72%，中证500的年化是5.55%

为什么最佳拟合直线和首尾点计算的年化差异这么大？还是因为今天2024年1月15日，收盘价跟最佳拟合直线的差距很大，自然会有很大的偏差，如果哪天能所谓的“价值回归”或是就应该是这个价，那2者会慢慢合理起来。

波动很大，但是最终的结果，还是能达到5%左右的年化收益率。