全排列の递归实现[C++实现]

一、有能力最好先读代码(C++)

#include <iostream>
#include <vector>
using namespace std;

void print(vector<int> arr) {
	int Size = arr.size();
	for (int i = 0; i < Size; i++) {
		cout << arr[i] << ' ';
	}cout << endl;
}

void permutation(vector<int>& arr, int k) {
	if (k == arr.size() - 1) print(arr);    //固定到最后一个数结束递归
	else {
		for (int i = k; i < arr.size() - 1; i++) {
			swap(arr[k], arr[i]);			//固定 
			permutation(arr, k + 1);        //递归
			swap(arr[k], arr[i]);			//还原 
		}
	}
}

int main() {
	vector<int> arr;
	for (int i = 1; i < 4; i++) {
		arr.push_back(i);
	}
	permutation(arr, 1);                    //测试全排列算法！
} 

二、思路过程

? ? ? ? 其实全排列递归过程没有你想的那么难。

? ? ? ? 回想一下高中时期，最初学排列组合时候，我们借助了演示图来学习。

排列组合演示

? ? ? ? ?想要弄懂全排列算法，不要上来就去想着硬凑的算法，一定要弄懂这张图，研究他们之间的递推关系，这样自然而来就能理解全排列从而很容易地去设计出全排列算法。

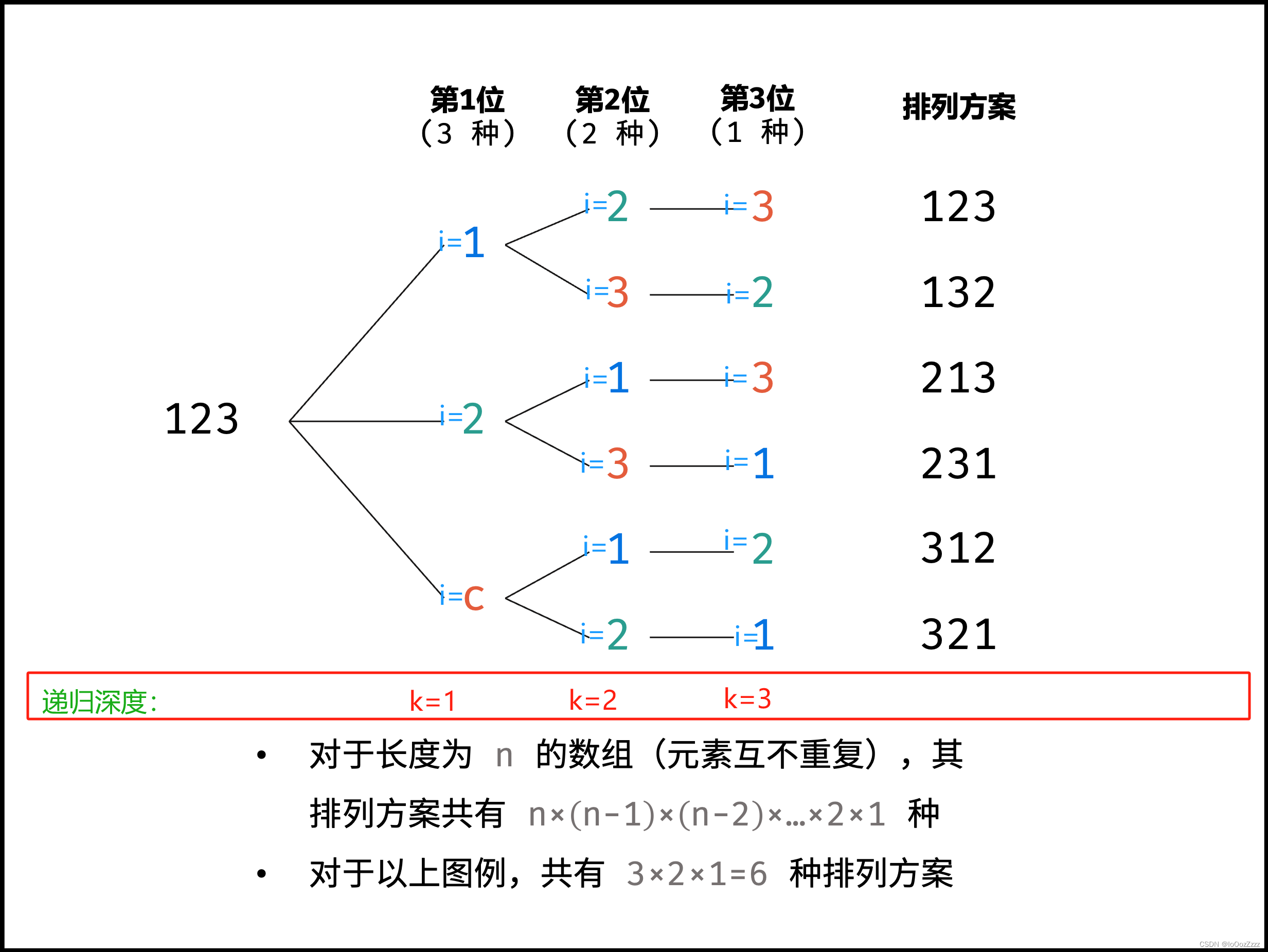
找到其中的规律：

? ? ? ? 就123这个序列而言，固定三次，分别为k=1, k=2, k=3。下一次固定，已经固定好的数字就不用继续固定了，固定剩下的数字即可。（k其实就代表的现在固定的是第几个数字）

? ? ? ? 要实现这个算法，在k=1时，我们必然要固定1， 2， 3三个数字。所以我们设计一个循环，用 i 这个变量去遍历k到最后一个数。

? ? ? ? 下一步，为了实现固定，将循环遍历的这个数字与第k位去交换。然后进入下一层递归，没错，这个过程每一步的思路都是重复的，递归条件成立！

? ? ? ? 因为循环还要接着遍历下一个数字，所以再次交换第 k 个数字和 i 位的数字，让数组回到原来的位置（这一步请动手画图自行理解，不难！）