团灭 LeetCode 股票买卖问题

这几道题目是有共性的，我们只需要抽出来力扣第 188 题「188. 买卖股票的最佳时机 IV - 力扣（LeetCode）」进行研究，因为这道题是最泛化的形式，其他的问题都是这个形式的简化，看下题目：

第一题是只进行一次交易，相当于 k = 1；第二题是不限交易次数，相当于 k = +infinity（正无穷）；第三题是只进行 2 次交易，相当于 k = 2；剩下两道也是不限次数，但是加了交易「冷冻期」和「手续费」的额外条件，其实就是第二题的变种，都很容易处理。

下面言归正传，开始解题。

穷举框架

首先，还是一样的思路：如何穷举？

动态规划算法本质上就是穷举「状态」，然后在「选择」中选择最优解。

那么对于这道题，我们具体到每一天，看看总共有几种可能的「状态」，再找出每个「状态」对应的「选择」。我们要穷举所有「状态」，穷举的目的是根据对应的「选择」更新状态。听起来抽象，你只要记住「状态」和「选择」两个词就行，下面实操一下就很容易明白了。

for 状态1 in 状态1的所有取值：
    for 状态2 in 状态2的所有取值：
        for ...
            dp[状态1][状态2][...] = 择优(选择1，选择2...)

比如说这个问题，每天都有三种「选择」：买入、卖出、无操作，我们用 buy, sell, rest 表示这三种选择。

但问题是，并不是每天都可以任意选择这三种选择的，因为 sell 必须在 buy 之后，buy 必须在 sell 之后。那么 rest 操作还应该分两种状态，一种是 buy 之后的 rest（持有了股票），一种是 sell 之后的 rest（没有持有股票）。而且别忘了，我们还有交易次数 k 的限制，就是说你 buy 还只能在 k > 0 的前提下操作。

注：

注意我在本文会频繁使用「交易」这个词，我们把一次买入和一次卖出定义为一次「交易」。

这个问题的「状态」有三个，第一个是天数，第二个是允许交易的最大次数，第三个是当前的持有状态（即之前说的 rest 的状态，我们不妨用 1 表示持有，0 表示没有持有）。然后我们用一个三维数组就可以装下这几种状态的全部组合：

dp[i][k][0 or 1]
0 <= i <= n - 1, 1 <= k <= K
n 为天数，大 K 为交易数的上限，0 和 1 代表是否持有股票。
此问题共 n × K × 2 种状态，全部穷举就能搞定。

for 0 <= i < n:
    for 1 <= k <= K:
        for s in {0, 1}:
            dp[i][k][s] = max(buy, sell, rest)

而且我们可以用自然语言描述出每一个状态的含义，比如说 dp[3][2][1] 的含义就是：今天是第三天，我现在手上持有着股票，至今最多进行 2 次交易。再比如 dp[2][3][0] 的含义：今天是第二天，我现在手上没有持有股票，至今最多进行 3 次交易。很容易理解，对吧？

我们想求的最终答案是 dp[n - 1][K][0]，即最后一天，最多允许 K 次交易，最多获得多少利润。

你可能问为什么不是 dp[n - 1][K][1]？因为 dp[n - 1][K][1] 代表到最后一天手上还持有股票，dp[n - 1][K][0] 表示最后一天手上的股票已经卖出去了，很显然后者得到的利润一定大于前者。

记住如何解释「状态」，一旦你觉得哪里不好理解，把它翻译成自然语言就容易理解了。

状态转移框架

现在，我们完成了「状态」的穷举，我们开始思考每种「状态」有哪些「选择」，应该如何更新「状态」。

只看「持有状态」，可以画个状态转移图：

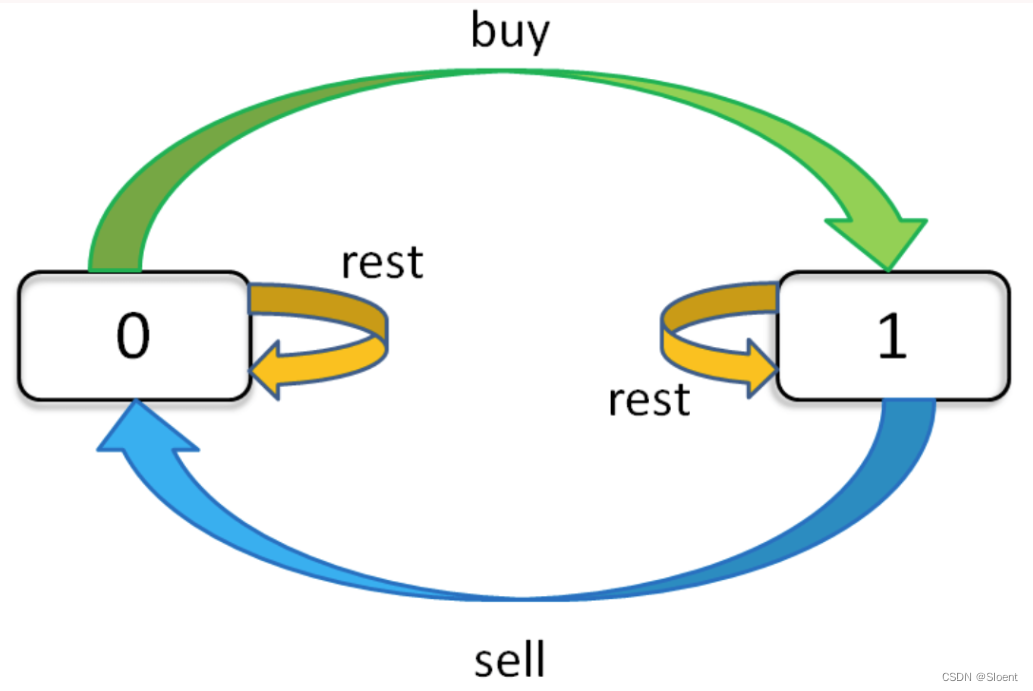
通过这个图可以很清楚地看到，每种状态（0 和 1）是如何转移而来的。根据这个图，我们来写一下状态转移方程：

dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])
              max( 今天选择 rest,        今天选择 sell       )

解释：今天我没有持有股票，有两种可能，我从这两种可能中求最大利润：

1、我昨天就没有持有，且截至昨天最大交易次数限制为 k；然后我今天选择 rest，所以我今天还是没有持有，最大交易次数限制依然为 k。

2、我昨天持有股票，且截至昨天最大交易次数限制为 k；但是今天我 sell 了，所以我今天没有持有股票了，最大交易次数限制依然为 k。

dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i])
              max( 今天选择 rest,         今天选择 buy         )

解释：今天我持有着股票，最大交易次数限制为 k，那么对于昨天来说，有两种可能，我从这两种可能中求最大利润：

1、我昨天就持有着股票，且截至昨天最大交易次数限制为 k；然后今天选择 rest，所以我今天还持有着股票，最大交易次数限制依然为 k。

2、我昨天本没有持有，且截至昨天最大交易次数限制为 k - 1；但今天我选择 buy，所以今天我就持有股票了，最大交易次数限制为 k。

注

这里着重提醒一下，时刻牢记「状态」的定义，状态 k 的定义并不是「已进行的交易次数」，而是「最大交易次数的上限限制」。如果确定今天进行一次交易，且要保证截至今天最大交易次数上限为 k，那么昨天的最大交易次数上限必须是 k - 1。举个具体的例子，比方说要求你的银行卡里今天至少有 100 块钱，且你确定你今天可以赚 10 块钱，那么你就要保证昨天的银行卡要至少剩下 90 块钱。

这个解释应该很清楚了，如果 buy，就要从利润中减去 prices[i]，如果 sell，就要给利润增加 prices[i]。今天的最大利润就是这两种可能选择中较大的那个。

注意 k 的限制，在选择 buy 的时候相当于开启了一次交易，那么对于昨天来说，交易次数的上限 k 应该减小 1。

现在，我们已经完成了动态规划中最困难的一步：状态转移方程。如果之前的内容你都可以理解，那么你已经可以秒杀所有问题了，只要套这个框架就行了。不过还差最后一点点，就是定义 base case，即最简单的情况。

dp[-1][...][0] = 0
解释：因为 i 是从 0 开始的，所以 i = -1 意味着还没有开始，这时候的利润当然是 0。

dp[-1][...][1] = -infinity
解释：还没开始的时候，是不可能持有股票的。
因为我们的算法要求一个最大值，所以初始值设为一个最小值，方便取最大值。

dp[...][0][0] = 0
解释：因为 k 是从 1 开始的，所以 k = 0 意味着根本不允许交易，这时候利润当然是 0。

dp[...][0][1] = -infinity
解释：不允许交易的情况下，是不可能持有股票的。
因为我们的算法要求一个最大值，所以初始值设为一个最小值，方便取最大值。

把上面的状态转移方程总结一下：

base case：
dp[-1][...][0] = dp[...][0][0] = 0
dp[-1][...][1] = dp[...][0][1] = -infinity

状态转移方程：
dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])
dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i])

秒杀题目

121. 买卖股票的最佳时机

第一题，先说力扣第 121 题「121. 买卖股票的最佳时机 - 力扣（LeetCode）」，相当于 k = 1 的情况：

直接套状态转移方程，根据 base case，可以做一些化简：

dp[i][1][0] = max(dp[i-1][1][0], dp[i-1][1][1] + prices[i])
dp[i][1][1] = max(dp[i-1][1][1], dp[i-1][0][0] - prices[i]) 
            = max(dp[i-1][1][1], -prices[i])
解释：k = 0 的 base case，所以 dp[i-1][0][0] = 0。

现在发现 k 都是 1，不会改变，即 k 对状态转移已经没有影响了。
可以进行进一步化简去掉所有 k：
dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
dp[i][1] = max(dp[i-1][1], -prices[i])

int n = prices.length;
int[][] dp = new int[n][2];
for (int i = 0; i < n; i++) {
    dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1] + prices[i]);
    dp[i][1] = Math.max(dp[i-1][1], -prices[i]);
}
return dp[n - 1][0];

显然 i = 0 时 i - 1 是不合法的索引，这是因为我们没有对 i 的 base case 进行处理，可以这样给一个特化处理：

if (i - 1 == -1) {
    dp[i][0] = 0;
    // 根据状态转移方程可得：
    //   dp[i][0] 
    // = max(dp[-1][0], dp[-1][1] + prices[i])
    // = max(0, -infinity + prices[i]) = 0

    dp[i][1] = -prices[i];
    // 根据状态转移方程可得：
    //   dp[i][1] 
    // = max(dp[-1][1], dp[-1][0] - prices[i])
    // = max(-infinity, 0 - prices[i]) 
    // = -prices[i]
    continue;
}

第一题就解决了，但是这样处理 base case 很麻烦，而且注意一下状态转移方程，新状态只和相邻的一个状态有关，不需要用整个 dp 数组，只需要一个变量储存相邻的那个状态就足够了，这样可以把空间复杂度降到 O(1):

// 原始版本
int maxProfit_k_1(int[] prices) {
    int n = prices.length;
    int[][] dp = new int[n][2];
    for (int i = 0; i < n; i++) {
        if (i - 1 == -1) {
            // base case
            dp[i][0] = 0;
            dp[i][1] = -prices[i];
            continue;
        }
        dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1] + prices[i]);
        dp[i][1] = Math.max(dp[i-1][1], -prices[i]);
    }
    return dp[n - 1][0];
}

// 空间复杂度优化版本
int maxProfit_k_1(int[] prices) {
    int n = prices.length;
    // base case: dp[-1][0] = 0, dp[-1][1] = -infinity
    int dp_i_0 = 0, dp_i_1 = Integer.MIN_VALUE;
    for (int i = 0; i < n; i++) {
        // dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
        dp_i_0 = Math.max(dp_i_0, dp_i_1 + prices[i]);
        // dp[i][1] = max(dp[i-1][1], -prices[i])
        dp_i_1 = Math.max(dp_i_1, -prices[i]);
    }
    return dp_i_0;
}

122. 买卖股票的最佳时机 II

第二题，看一下力扣第 122 题「122. 买卖股票的最佳时机 II - 力扣（LeetCode）」，也就是 k 为正无穷的情况：

题目还专门强调可以在同一天出售，但我觉得这个条件纯属多余，如果当天买当天卖，那利润当然就是 0，这不是和没有进行交易是一样的吗？这道题的特点在于没有给出交易总数 k 的限制，也就相当于 k 为正无穷。

如果 k 为正无穷，那么就可以认为 k 和 k - 1 是一样的。可以这样改写框架：

dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])
dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i])
            = max(dp[i-1][k][1], dp[i-1][k][0] - prices[i])

我们发现数组中的 k 已经不会改变了，也就是说不需要记录 k 这个状态了：
dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
dp[i][1] = max(dp[i-1][1], dp[i-1][0] - prices[i])

// 原始版本
int maxProfit_k_inf(int[] prices) {
    int n = prices.length;
    int[][] dp = new int[n][2];
    for (int i = 0; i < n; i++) {
        if (i - 1 == -1) {
            // base case
            dp[i][0] = 0;
            dp[i][1] = -prices[i];
            continue;
        }
        dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1] + prices[i]);
        dp[i][1] = Math.max(dp[i-1][1], dp[i-1][0] - prices[i]);
    }
    return dp[n - 1][0];
}

// 空间复杂度优化版本
int maxProfit_k_inf(int[] prices) {
    int n = prices.length;
    int dp_i_0 = 0, dp_i_1 = Integer.MIN_VALUE;
    for (int i = 0; i < n; i++) {
        int temp = dp_i_0;
        dp_i_0 = Math.max(dp_i_0, dp_i_1 + prices[i]);
        dp_i_1 = Math.max(dp_i_1, temp - prices[i]);
    }
    return dp_i_0;
}

123. 买卖股票的最佳时机 III

第三题，看力扣第 123 题「123. 买卖股票的最佳时机 III - 力扣（LeetCode）」，也就是 k = 2 的情况：

k = 2 和前面题目的情况稍微不同，因为上面的情况都和 k 的关系不太大：要么 k 是正无穷，状态转移和 k 没关系了；要么 k = 1，跟 k = 0 这个 base case 挨得近，最后也没有存在感。

这道题 k = 2 和后面要讲的 k 是任意正整数的情况中，对 k 的处理就凸显出来了，我们直接写代码，边写边分析原因。

原始的状态转移方程，没有可化简的地方
dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])
dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i])

按照之前的代码，我们可能想当然这样写代码（错误的）：

int k = 2;
int[][][] dp = new int[n][k + 1][2];
for (int i = 0; i < n; i++) {
    if (i - 1 == -1) {
        // 处理 base case
        dp[i][k][0] = 0;
        dp[i][k][1] = -prices[i];
        continue;
    }
    dp[i][k][0] = Math.max(dp[i-1][k][0], dp[i-1][k][1] + prices[i]);
    dp[i][k][1] = Math.max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i]);
}
return dp[n - 1][k][0];

为什么错误？我这不是照着状态转移方程写的吗？

还记得前面总结的「穷举框架」吗？就是说我们必须穷举所有状态。其实我们之前的解法，都在穷举所有状态，只是之前的题目中 k 都被化简掉了。

比如说第一题，k = 1 时的代码框架：

int n = prices.length;
int[][] dp = new int[n][2];
for (int i = 0; i < n; i++) {
    dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1] + prices[i]);
    dp[i][1] = Math.max(dp[i-1][1], -prices[i]);
}
return dp[n - 1][0];

但当 k = 2 时，由于没有消掉 k 的影响，所以必须要对 k 进行穷举：

// 原始版本
int maxProfit_k_2(int[] prices) {
    int max_k = 2, n = prices.length;
    int[][][] dp = new int[n][max_k + 1][2];
    for (int i = 0; i < n; i++) {
        for (int k = max_k; k >= 1; k--) {
            if (i - 1 == -1) {
                // 处理 base case
                dp[i][k][0] = 0;
                dp[i][k][1] = -prices[i];
                continue;
            }
            dp[i][k][0] = Math.max(dp[i-1][k][0], dp[i-1][k][1] + prices[i]);
            dp[i][k][1] = Math.max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i]);
        }
    }
    // 穷举了 n × max_k × 2 个状态，正确。
    return dp[n - 1][max_k][0];
}

注

这里肯定会有读者疑惑，k 的 base case 是 0，按理说应该从 k = 1, k++ 这样穷举状态 k 才对？而且如果你真的这样从小到大遍历 k，提交发现也是可以的。

为什么我从大到小遍历 k 也可以正确提交呢？因为你注意看，dp[i][k][..] 不会依赖 dp[i][k - 1][..]，而是依赖 dp[i - 1][k - 1][..]，而 dp[i - 1][..][..]，都是已经计算出来的，所以不管你是 k = max_k, k--，还是 k = 1, k++，都是可以得出正确答案的。

那为什么我使用 k = max_k, k-- 的方式呢？因为这样符合语义：

你买股票，初始的「状态」是什么？应该是从第 0 天开始，而且还没有进行过买卖，所以最大交易次数限制 k 应该是 max_k；而随着「状态」的推移，你会进行交易，那么交易次数上限 k 应该不断减少，这样一想，k = max_k, k-- 的方式是比较合乎实际场景的。

当然，这里 k 取值范围比较小，所以也可以不用 for 循环，直接把 k = 1 和 2 的情况全部列举出来也可以：

// 状态转移方程：
// dp[i][2][0] = max(dp[i-1][2][0], dp[i-1][2][1] + prices[i])
// dp[i][2][1] = max(dp[i-1][2][1], dp[i-1][1][0] - prices[i])
// dp[i][1][0] = max(dp[i-1][1][0], dp[i-1][1][1] + prices[i])
// dp[i][1][1] = max(dp[i-1][1][1], -prices[i])

// 空间复杂度优化版本
int maxProfit_k_2(int[] prices) {
    // base case
    int dp_i10 = 0, dp_i11 = Integer.MIN_VALUE;
    int dp_i20 = 0, dp_i21 = Integer.MIN_VALUE;
    for (int price : prices) {
        dp_i20 = Math.max(dp_i20, dp_i21 + price);
        dp_i21 = Math.max(dp_i21, dp_i10 - price);
        dp_i10 = Math.max(dp_i10, dp_i11 + price);
        dp_i11 = Math.max(dp_i11, -price);
    }
    return dp_i20;
}