Day24_77 组合

77 组合

1. 组合无序，排列有序。
2. 1~n个数中选k个数组合，k不确定，组合的方式。
   
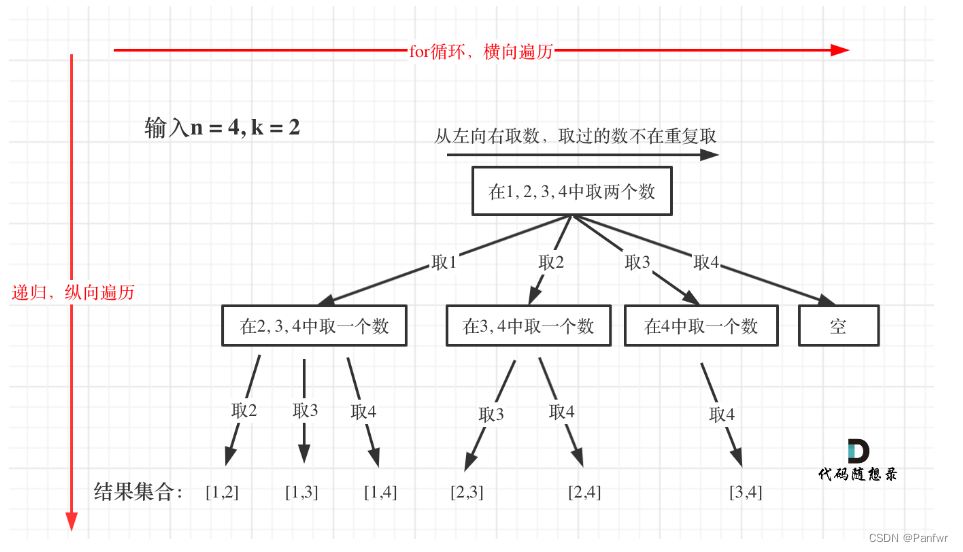
   （图片来自代码随想录）
3. 确定回溯法的三部曲：

• 递归函数的返回值和参数：集合n中取k个数，，每次从不同的位置开始，定义startIndex调整可以选择的范围[startIndex, n]。需要记录所有的组合和每次的组合数，定义两个全局变量记录每一个组合的vector<int> path和记录所有组合结果的vector<int> result。
• 确定回溯函数的终止条件：path.size() == k; result.push_back(path)。
• 确定回溯单层搜索逻辑：

for(int i = startIndex; i <= n; i++){//控制树的横向遍历
	path.push_back(i);//处理节点
	backtracking(n, k, i+1);//控制树的纵向遍历，从i+1开始
	path.pop_back();//回溯，撤销现在处理的节点，处理下一个节点
}

4. 对于组合总数小于k（比如4）如何处理？处理过程跳过if判断，跳过for的循环，执行backtracking结束，隐含一个return的结束。

组合的修剪

1. 如何修剪：for循环选择的起始位置之后的元素个数 已经不足 我们需要的元素个数了，那么就没有必要搜索了。
2. n：总数，k：组合数，path.size()：已经加入组合的元素个数，（k-path.size()）：还需要组合的数，n-(k-path.size())+1：满足组合总数为k的最低开始位置。
3. 确定修剪的代码：

for(int i = startIndex; i <= n-(k-path.size()); i++){
	path.push_back(i);
	backtracking(n, k, i+1);
	path.pop_back();
}