C/C++ BM4 合并两个排序的链表
前言
这道题采用两种方式,一种是直接插入法,还有一种就是递归调用。
题目
输入两个递增的链表,单个链表的长度为n,合并这两个链表并使新链表中的节点仍然是递增排序的。
数据范围: 0≤n≤1000,?1000≤节点值≤1000
要求:空间复杂度 O(1),时间复杂度 O(n
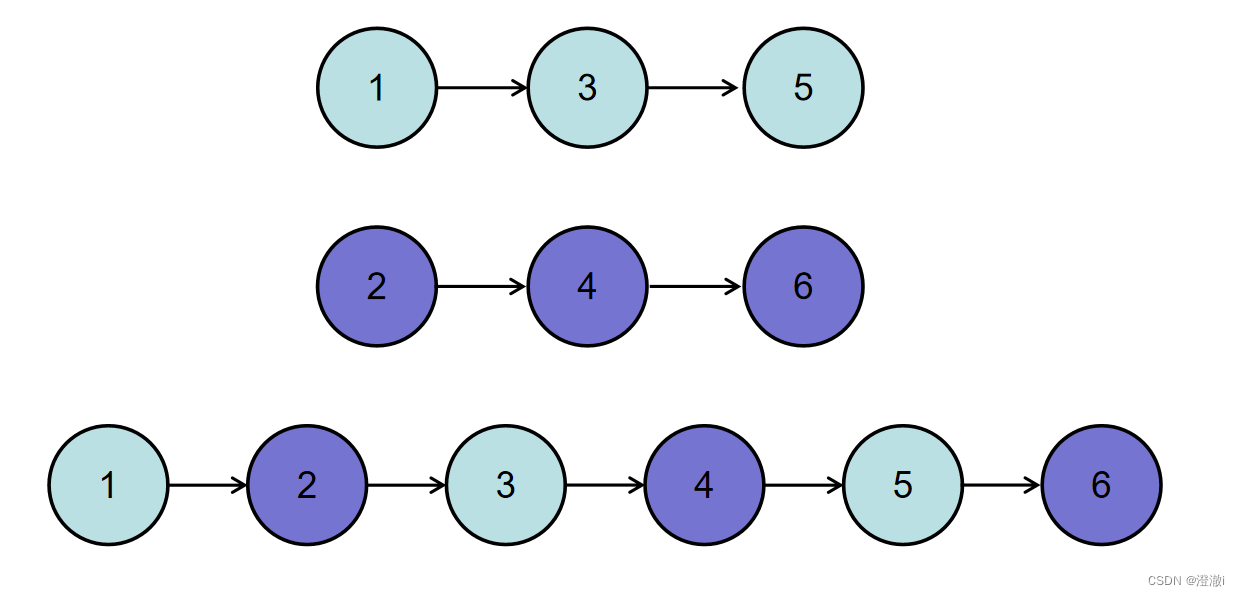
如输入{1,3,5},{2,4,6}时,合并后的链表为{1,2,3,4,5,6},所以对应的输出为{1,2,3,4,5,6},转换过程如下图所示:
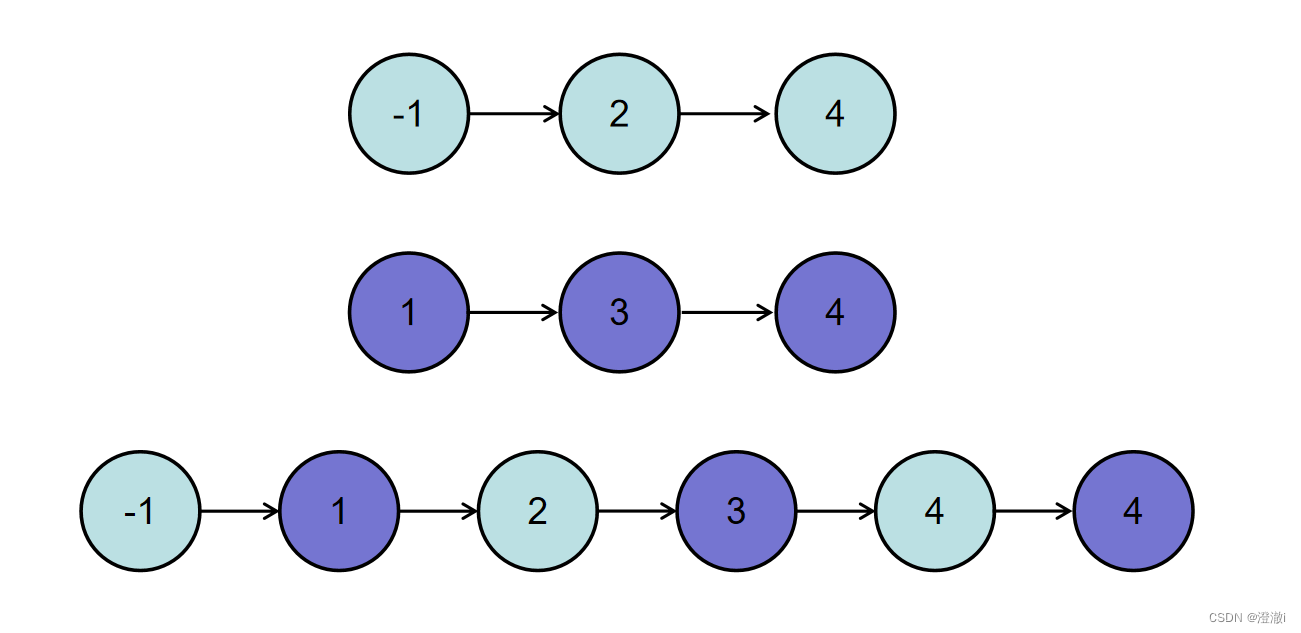
或输入{-1,2,4},{1,3,4}时,合并后的链表为{-1,1,2,3,4,4},所以对应的输出为{-1,1,2,3,4,4},转换过程如下图所示:

1. 解决方案一
1.1 思路概述
合并链表的过程就是插入节点的过程,不过是双链表遍历。
首先判断两个链表的最小节点谁的最小,那么链表首节点小的作为基链表,另一个链表进行比较与插入。
一般链表题都要添加一个头结点,作为哨兵节点,这样的好处是确保每一个节点都有一个前置节点。
对于题目中的特殊情况,空链表这种,我们得单独拎出来判断。如果一个链表是空链表,则直接返回另一个非空链表;如果两个链表都为空,则直接返回空链表。
正常判断的情况,这里以pHead1为基链表的情况(也就是pHead1的第一个节点小于pHead2的第一个节点)为例。
我们通过一个bool类型变量来确定基链表判断逻辑。
如果pHead2链表的值小于pHead1指向的节点的下一个值,就进行插入。比如,1,3,5的基链表,2,4,6链表往里面插入,因为我们已经通过首节点判断出pHead2的首节点肯定比pHead1的节点大,我们只需要找到pHead1中第一个比pHead2中要插入到pHead1的节点大的节点即可。所以这里用到了pHead->next->val。
后面就是断链和插入的操作,再接着就是双链表遍历,即调整双链表中指针的位置。
如果pHead1>pHead2的情况,那么逻辑是基本一致的,这里就不在赘述。
1.2 源码
/**
* struct ListNode {
* int val;
* struct ListNode *next;
* ListNode(int x) : val(x), next(nullptr) {}
* };
*/
class Solution {
public:
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param pHead1 ListNode类
* @param pHead2 ListNode类
* @return ListNode类
*/
ListNode* Merge(ListNode* pHead1, ListNode* pHead2) {
ListNode* rec = new ListNode(-1);
if (!pHead1 && !pHead2) {
return nullptr;
}
if (!pHead1 && pHead2) {
return pHead2;
}
if (pHead1 && !pHead2) {
return pHead1;
}
//比较链表大小
bool firstListBig = true;
if (pHead1->val > pHead2->val) {
firstListBig = true;
rec->next = pHead2;
} else {
firstListBig = false;
rec->next = pHead1;
}
//第二个链表大的情况
if (!firstListBig) {
while (pHead2 && pHead1) {
//如果小链表后面没有节点了,则大链表直接加到小链表后
if (!pHead1->next) {
pHead1->next = pHead2;
break;
}
ListNode* tempNode = pHead2->next;
if (pHead2->val <= pHead1->next->val) {
pHead2->next = pHead1->next;
pHead1->next = pHead2;
pHead2 = tempNode;
pHead1 = pHead1->next;
} else {
pHead1 = pHead1->next;
if (!pHead1->next) {
pHead1->next = pHead2;
break;
}
}
}
}
else //第二个链表小的情况
{
while (pHead2 && pHead1) {
if (!pHead2->next) {
pHead2->next = pHead1;
break;
}
ListNode* tempNode = pHead1->next;
if (pHead1->val <= pHead2->next->val) {
pHead1->next = pHead2->next;
pHead2->next = pHead1;
pHead1 = tempNode;
pHead2 = pHead2->next;
} else {
pHead2 = pHead2->next;
if (!pHead2->next) {
pHead2->next = pHead1;
break;
}
}
}
}
return rec->next;
}
};
2. 解决方案二
2.1 思路阐述
使用递归的方式进行处理。
写递归代码,最重要的要明白递归函数的功能。可以不必关心递归函数的具体实现。
比如这个ListNode* Merge(ListNode* pHead1, ListNode* pHead2)
函数功能:合并两个单链表,返回两个单链表头结点值小的那个节点。
如果知道了这个函数功能,那么接下来需要考虑2个问题:
递归函数结束的条件是什么?(这个非常重要,一般第一个就要写它)
递归函数一定是缩小递归区间的,那么下一步的递归区间是什么?
对于问题1.对于链表就是,如果为空,返回什么
对于问题2,跟迭代方法中的一样,如果PHead1的所指节点值小于等于pHead2所指的结点值,那么phead1后续节点和pHead节点继续递归。这个就类似于去找到一个pHead1中所指节点第一个比pHead2所指节点大的节点。
时间复杂度:O(m+n)
空间复杂度:O(m+n),每一次递归,递归栈都会保存一个变量,最差情况会保存(m+n)个变量
递归的一个大致流程,我画了一下,其实大家可以自己debug一下就知道了

2.2 源码
class Solution {
public:
ListNode* Merge(ListNode* pHead1, ListNode* pHead2)
{
if (!pHead1) return pHead2;
if (!pHead2) return pHead1;
if (pHead1->val <= pHead2->val) {
pHead1->next = Merge(pHead1->next, pHead2);
return pHead1;
}
else {
pHead2->next = Merge(pHead1, pHead2->next);
return pHead2;
}
}
};
总结
这道题的第一个迭代方法是我最先想到的,代码也比较好写。第二个方法是看题解,这里整合下来作为参考。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- react 实现页面状态缓存(keep-alive)
- 揭秘安全测试--一起学习吧之安全测试
- OWASP漏洞原理启航(第一课)
- 2023年山东省职业院校技能大赛高职组 “软件测试”赛项竞赛任务四 单元测试
- FreeRTOS——队列及其实战
- Mybatis简易搭建并查询数据库表内所有数据
- django电子商务网站的设计与实现(程序+开题报告)
- 汇川PLC与工业远程透传模块远程上下载程序
- FL Studio2024mac电脑版本下载步骤教程
- thinkadmin上传excel导入数据库