【PyTorch】在PyTorch中使用线性层和交叉熵损失函数进行数据分类

发布时间：2024年01月17日

在PyTorch中使用线性层和交叉熵损失函数进行数据分类

前言：

在机器学习的众多任务中，分类问题无疑是最基础也是最重要的一环。本文将介绍如何在PyTorch框架下，使用线性层和交叉熵损失函数来解决分类问题。我们将以简单的Iris数据集作为起点，探讨线性模型在处理线性可分数据上的有效性。随后，我们将尝试将同样的线性模型应用于复杂的CIFAR-10图像数据集，并分析其性能表现。

背景：

Iris数据集：一个经典的线性可分数据集，包含三个类别的鸢尾花，每个类别有50个样本，每个样本有4个特征。
CIFAR-10数据集：一个由10个类别组成的图像数据集，每个类别有6000张32x32彩色图像，总共有60000张图像。

Iris数据集分类

数据读取与预处理：

read_data函数负责从CSV文件中读取数据，随机打乱，划分训练集和测试集，并进行标准化处理。

def read_data(file_path, only_test = False, normalize = True):
    np_data = pd.read_csv(file_path).values
    np.random.shuffle(np_data)
    
    classes = np.unique(np_data[:,-1])
    class_dict = {}
    for index, class_name in enumerate(classes):
        class_dict[index] = class_name
        class_dict[class_name] = index
        
    train_src = np_data[:int(len(np_data)*0.8)]
    test_src = np_data[int(len(np_data)*0.8):]
    train_data = train_src[:,:-1]
    train_labels = train_src[:, -1].reshape(-1,1)
    test_data = test_src[:, :-1]
    test_labels = test_src[:, -1].reshape(-1,1)
    if (normalize):
        mean = np.mean(train_data)
        std = np.std(train_data)
        train_data = (train_data - mean) / std
        mean = np.mean(test_data)
        std = np.std(test_data)
        test_data = (test_data - mean) / std
    if (only_test):
        return test_data, test_labels, class_dict
    return train_data, train_labels, test_data, test_labels, class_dict

模型构建：

Linear_classify类定义了一个简单的线性模型，其中包含一个线性层。

class Linear_classify(th.nn.Module):
    def __init__(self, *args, **kwargs) -> None:
        super(Linear_classify, self).__init__()
        self.linear = th.nn.Linear(args[0], args[1])
        
    def forward(self, x):
        y_pred = self.linear(x)
        return y_pred

训练过程：在`main`函数中，我们初始化模型、损失函数和优化器。然后，通过多次迭代来训练模型，并记录损失值的变化。

file_path = "J:\\MachineLearning\\数据集\\Iris\\iris.data"
train_data, train_labels, test_data, test_labels, label_dict = read_data(file_path)
print(train_data.shape)
print(train_labels.shape)
print(label_dict)

int_labels = np.vectorize(lambda x: int(label_dict[x]))(train_labels).flatten()
print(int_labels[:10])

tensor_labels = th.from_numpy(int_labels).type(th.long) 
num_classes = int(len(label_dict)/2)
train_data = th.from_numpy(train_data.astype("float32"))

print (train_data.shape)
print (train_data[:2])
linear_classifier = Linear_classify(int(train_data.shape[1]), int(len(label_dict)/2))
loss_function = th.nn.CrossEntropyLoss()
optimizer = th.optim.SGD(linear_classifier.parameters(), lr = 0.001)
epochs = 10000
best_loss = 100
turn_to_bad_loss_count = 0
loss_history = []
for epoch in range(epochs):
    y_pred = linear_classifier(train_data)
    #print(y_pred)
    #print(y_pred.shape)
    loss = loss_function(y_pred, tensor_labels)
    if (float(loss.item()) > best_loss):
        turn_to_bad_loss_count += 1
    else:
        best_loss = float(loss.item())
    if (turn_to_bad_loss_count > 1000):
        break
    if (epoch % 10 == 0):
        print("epoch {} loss is {}".format(epoch, loss))
        loss_history.append(float(loss.item()))
    loss.backward()
    optimizer.step()
plt.plot(loss_history)
plt.show()

评估与测试

使用测试集数据评估模型的准确率，并通过可视化损失值的变化来分析模型的学习过程。

accuracy = []
for _ in range(10):
    test_data, test_labels, label_dict = read_data(file_path, only_test = True)
    test_result = linear_classifier(th.from_numpy(test_data.astype("float32")))
    print(test_result[:10])
    
    result_index = test_result.argmax(dim=1)
    iris_name_result = np.vectorize(lambda x: str(label_dict[x]))(result_index).reshape(-1,1)
    accuracy.append(len(iris_name_result[iris_name_result == test_labels]) / len(test_labels))
    
print("Accuracy is {}".format(np.mean(accuracy)))

结果

收敛很好很快

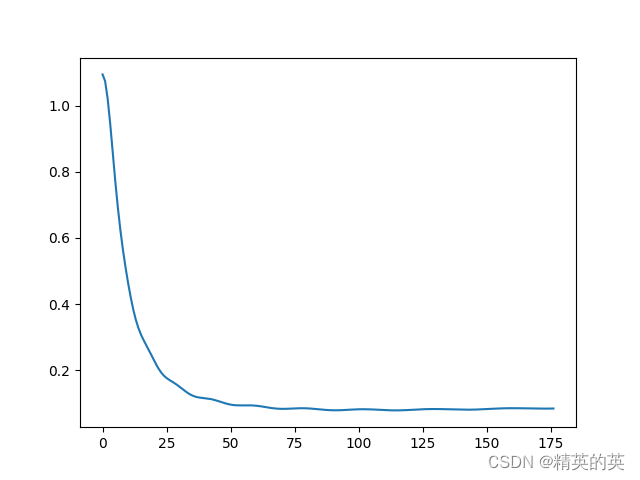
请添加图片描述

准确率较高

Accuracy is 0.9466666666666667

CIFAR-10数据集分类

关键改动

使用unpickle和read_data函数处理数据集，这部分是和前面不一样的

def unpickle(file):
    import pickle
    with open(file, 'rb') as fo:
        dict = pickle.load(fo, encoding='bytes')
    return dict

def read_data(file_path, gray = False, percent = 0, normalize = True):
    data_src = unpickle(file_path)
    np_data = np.array(data_src["data".encode()]).astype("float32")
    np_labels = np.array(data_src["labels".encode()]).astype("float32").reshape(-1,1)
    single_data_length = 32*32 
    image_ret = None
    if (gray):
        np_data = (np_data[:, :single_data_length] + np_data[:, single_data_length:(2*single_data_length)] + np_data[:, 2*single_data_length : 3*single_data_length])/3
        image_ret = np_data.reshape(len(np_data),32,32)
    else:
        image_ret = np_data.reshape(len(np_data),32,32,3)
    
    if(normalize):
        mean = np.mean(np_data)
        std = np.std(np_data)
        np_data = (np_data - mean) / std
    if (percent == 0):
        return np_data, np_labels, image_ret 
    else:
        return np_data[:int(len(np_data)*percent)], np_labels[:int(len(np_labels)*percent)], image_ret[:int(len(image_ret)*percent)]

运行结果

损失可以收敛，但收敛的幅度有限

可见只是从2.x 下降到了1.x
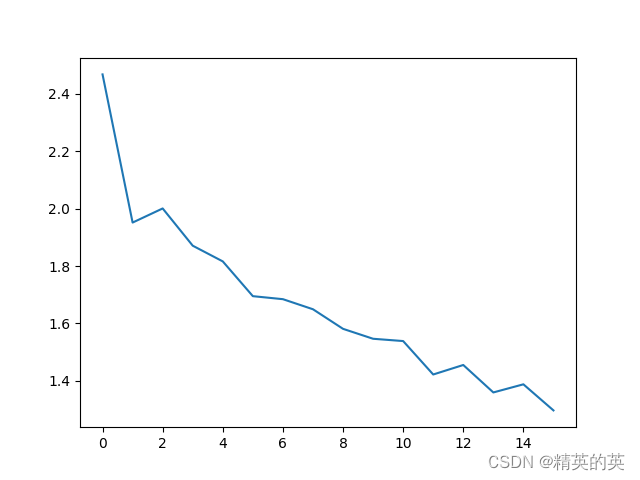
请添加图片描述

准确率比瞎猜准了3倍，非常的nice

请添加图片描述

train Accuracy is 0.6048

test Accuracy is 0.282

注意点：

数据标准化：为了提高模型的收敛速度和准确率，对数据进行标准化处理是非常重要的，在本例中，不使用标准化会出现梯度爆炸，亲测。
类别标签处理：在使用交叉熵损失函数时，需要确保类别标签是整数形式。

优化点：

学习率调整：适当调整学习率可以帮助模型更快地收敛。
早停法：当连续多次迭代损失值不再下降时，提前终止训练可以防止过拟合。
损失函数选择：对于不同的问题，选择合适的损失函数对模型性能有显著影响，在多分类问题中，使用交叉熵损失函数是常见的选择，在pytorch中，交叉熵模块包含了softmax激活函数，这是其可以进行多分类的关键。

Softmax函数的推导过程如下：

首先，我们有一个未归一化的输入向量 $z$ ，其形状为 $(n,)$ ，其中 $n$ 是类别的数量。我们希望将这个向量转化为一个概率分布，其中所有元素的总和为1。

我们可以通过以下步骤来计算 softmax 函数：

对 $z$ 中的每个元素应用指数函数，得到一个新的向量 $e^z$ 。
计算 $e^z$ 中的最大值，记作 $\hat{z}$ 。
对 $e^z$ 中的每个元素减去 $\hat{z}$ ，得到一个新的向量 $v$ 。
对 $v$ 中的每个元素应用指数函数，得到一个新的向量 $e^v$ 。
计算 $e^v$ 中的最大值，记作 $\hat{v}$ 。
对 $e^v$ 中的每个元素除以 $\hat{v}$ ，得到最终的概率分布。

以上步骤可以用以下的公式表示：

$\begin{align*} z &= (z_1, z_2, \ldots, z_n)^T \\ e^z &= (e^{z_1}, e^{z_2}, \ldots, e^{z_n})^T \\ \hat{z} &= max(e^z) \\ v &= e^z - \hat{z} \\ e^v &= (e^{v_1}, e^{v_2}, \ldots, e^{v_n})^T \\ \hat{v} &= max(e^v) \\ p &= \frac{e^v}{\hat{v}} \end{align*}$

其中， $p$ 是最终的概率分布。

结论：
通过实验，我们发现线性模型在Iris数据集上表现良好，但在CIFAR-10数据集上效果不佳。这说明线性模型在处理复杂的非线性问题时存在局限性。为了解决这一问题，我们将在后续的博客中介绍如何使用卷积神经网络来提高图像分类的准确率。

后记：
感谢您的阅读，希望本文能够帮助您了解如何在PyTorch中使用线性层和交叉熵损失函数进行数据分类。敬请期待我们的下一篇博客——“在PyTorch中使用卷积神经网络进行图像分类”。

完整代码

分类Iris数据集

import torch as th
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import torchvision

def read_data(file_path, only_test = False, normalize = True):
    np_data = pd.read_csv(file_path).values
    np.random.shuffle(np_data)
    
    classes = np.unique(np_data[:,-1])
    class_dict = {}
    for index, class_name in enumerate(classes):
        class_dict[index] = class_name
        class_dict[class_name] = index
        
    train_src = np_data[:int(len(np_data)*0.8)]
    test_src = np_data[int(len(np_data)*0.8):]
    train_data = train_src[:,:-1]
    train_labels = train_src[:, -1].reshape(-1,1)
    test_data = test_src[:, :-1]
    test_labels = test_src[:, -1].reshape(-1,1)
    if (normalize):
        mean = np.mean(train_data)
        std = np.std(train_data)
        train_data = (train_data - mean) / std
        mean = np.mean(test_data)
        std = np.std(test_data)
        test_data = (test_data - mean) / std
    if (only_test):
        return test_data, test_labels, class_dict
    return train_data, train_labels, test_data, test_labels, class_dict


class Linear_classify(th.nn.Module):
    def __init__(self, *args, **kwargs) -> None:
        super(Linear_classify, self).__init__()
        self.linear = th.nn.Linear(args[0], args[1])
        
    def forward(self, x):
        y_pred = self.linear(x)
        return y_pred



def main():
    file_path = "J:\\MachineLearning\\数据集\\Iris\\iris.data"
    train_data, train_labels, test_data, test_labels, label_dict = read_data(file_path)
    print(train_data.shape)
    print(train_labels.shape)
    print(label_dict)
    
    int_labels = np.vectorize(lambda x: int(label_dict[x]))(train_labels).flatten()
    print(int_labels[:10])
    
    tensor_labels = th.from_numpy(int_labels).type(th.long) 
    num_classes = int(len(label_dict)/2)
    train_data = th.from_numpy(train_data.astype("float32"))

    print (train_data.shape)
    print (train_data[:2])
    linear_classifier = Linear_classify(int(train_data.shape[1]), int(len(label_dict)/2))
    loss_function = th.nn.CrossEntropyLoss()
    optimizer = th.optim.SGD(linear_classifier.parameters(), lr = 0.001)
    epochs = 10000
    best_loss = 100
    turn_to_bad_loss_count = 0
    loss_history = []
    for epoch in range(epochs):
        y_pred = linear_classifier(train_data)
        #print(y_pred)
        #print(y_pred.shape)
        loss = loss_function(y_pred, tensor_labels)
        if (float(loss.item()) > best_loss):
            turn_to_bad_loss_count += 1
        else:
            best_loss = float(loss.item())
        if (turn_to_bad_loss_count > 1000):
            break
        if (epoch % 10 == 0):
            print("epoch {} loss is {}".format(epoch, loss))
            loss_history.append(float(loss.item()))
        loss.backward()
        optimizer.step()
    plt.plot(loss_history)
    plt.show()
    plt.show()
    
    accuracy = []
    for _ in range(10):
        test_data, test_labels, label_dict = read_data(file_path, only_test = True)
        test_result = linear_classifier(th.from_numpy(test_data.astype("float32")))
        print(test_result[:10])
        
        result_index = test_result.argmax(dim=1)
        iris_name_result = np.vectorize(lambda x: str(label_dict[x]))(result_index).reshape(-1,1)
        accuracy.append(len(iris_name_result[iris_name_result == test_labels]) / len(test_labels))
        
    print("Accuracy is {}".format(np.mean(accuracy)))
    
if (__name__ == "__main__"):
    main()

分类CIFAR-10数据集

import torch as th
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt


def unpickle(file):
    import pickle
    with open(file, 'rb') as fo:
        dict = pickle.load(fo, encoding='bytes')
    return dict



def read_data(file_path, gray = False, percent = 0, normalize = True):
    data_src = unpickle(file_path)
    np_data = np.array(data_src["data".encode()]).astype("float32")
    np_labels = np.array(data_src["labels".encode()]).astype("float32").reshape(-1,1)
    single_data_length = 32*32 
    image_ret = None
    if (gray):
        np_data = (np_data[:, :single_data_length] + np_data[:, single_data_length:(2*single_data_length)] + np_data[:, 2*single_data_length : 3*single_data_length])/3
        image_ret = np_data.reshape(len(np_data),32,32)
    else:
        image_ret = np_data.reshape(len(np_data),32,32,3)
    
    if(normalize):
        mean = np.mean(np_data)
        std = np.std(np_data)
        np_data = (np_data - mean) / std
    if (percent == 0):
        return np_data, np_labels, image_ret 
    else:
        return np_data[:int(len(np_data)*percent)], np_labels[:int(len(np_labels)*percent)], image_ret[:int(len(image_ret)*percent)]
    
        
        
    


class Linear_classify(th.nn.Module):
    def __init__(self, *args, **kwargs) -> None:
        super(Linear_classify, self).__init__()
        self.linear = th.nn.Linear(args[0], args[1])
        
        
    def forward(self, x):
        x = self.linear(x)
        return x



def main():
    file_path = "J:\\MachineLearning\\数据集\\cifar-10-batches-py\\data_batch_1"
    train_data, train_labels, image_data = read_data(file_path, percent=0.5)
    print(train_data.shape)
    print(train_labels.shape)
    print(image_data.shape)
    '''
    fig, axs = plt.subplots(3, 3)
    
    for i, ax in enumerate(axs.flat):
        image = image_data[i]
        ax.imshow(image_data[i],cmap="rgb")
        ax.axis('off') # 关闭坐标轴
    
    plt.show()
    '''
    
    int_labels = train_labels.flatten()
    print(int_labels[:10])
    
    tensor_labels = th.from_numpy(int_labels).type(th.long) 
    num_classes = int(len(np.unique(int_labels)))
    train_data = th.from_numpy(train_data)

    print (train_data.shape)
    print (train_data[:2])
    linear_classifier = Linear_classify(int(train_data.shape[1]), num_classes)
    loss_function = th.nn.CrossEntropyLoss()
    optimizer = th.optim.SGD(linear_classifier.parameters(), lr = 0.01)
    epochs = 7000
    best_loss = 100
    turn_to_bad_loss_count = 0
    loss_history = []
    for epoch in range(epochs):
        y_pred = linear_classifier(train_data)
        #print(y_pred)
        #print(y_pred.shape)
        loss = loss_function(y_pred, tensor_labels)
        if (float(loss.item()) > best_loss):
            turn_to_bad_loss_count += 1
        else:
            best_loss = float(loss.item())
        if (turn_to_bad_loss_count > 100):
            break
        if (epoch % 10 == 0):
            print("epoch {} loss is {}".format(epoch, loss))
            loss_history.append(float(loss.item()))
        loss.backward()
        optimizer.step()
    plt.plot(loss_history)
    plt.show()
    plt.show()
    
    test_result = linear_classifier(train_data)
    print(test_result[:10])
    result_index = test_result.argmax(dim=1).reshape(-1,1)
    accuracy = (len(result_index[result_index.detach().numpy() == train_labels]) / len(train_labels))
    print("train Accuracy is {}".format(accuracy))
    
    file_path = "J:\\MachineLearning\\数据集\\cifar-10-batches-py\\test_batch"
    test_data, test_labels, image_data = read_data(file_path)
    test_result = linear_classifier(th.from_numpy(test_data))
    print(test_result[:10])
    result_index = test_result.argmax(dim=1).reshape(-1,1)
    accuracy = (len(result_index[result_index.detach().numpy() == test_labels]) / len(test_labels))
        
    print("test Accuracy is {}".format(accuracy))
    
if (__name__ == "__main__"):
    main()

文章来源:https://blog.csdn.net/weixin_45568812/article/details/135639889
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！