机器学习---xgboost算法

1.?xgboost算法原理

XGBoost（Extreme Gradient Boosting）全名叫极端梯度提升树，XGBoost是集成学习方法的王

牌，在Kaggle数据挖掘比赛中，大部分获胜者用了XGBoost。 XGBoost在绝大多数的回归和分类

问题上表现的十分顶尖，本节将较详细的介绍XGBoost的算法原理。构建最优模型的?般方法是最

小化训练数据的损失函数。 我们用字母?L 表示损失，如下式：

其中，F是假设空间，假设空间是在已知属性和属性可能取值的情况下，对所有可能满足目标的情

况的?种毫无遗漏的假设集合。式（1.1）称为经验风险最小化，训练得到的模型复杂度较高。当

训练数据较小时，模型很容易出现过拟合问题。 因此，为了降低模型的复杂度，常采用下式：

。其中J(f)为模型的复杂度，式（2.1）称为结构风险

最小化，结构风险最小化的模型往往对训练数据以及未知的测试数据都有较好的预测。决策树的生

成和剪枝分别对应了经验风险最小化和结构风险最小化， XGBoost的决策树生成是结构风险最小

化的结果。

2. XGBoost的?标函数推导

目标函数，即损失函数，通过最小化损失函数来构建最优模型。 由前面可知， 损失函数应加上表

示模型复杂度的正则项，且XGBoost对应的模型包含了多个CART树，因此，模型的目标函数为：

，（3.1）式是正则化的损失函数； 其中 y 是模型的实际输

出结果， 是模型的输出结果； 等式右边第?部分是模型的训练误差，第?部分是正则化项，这里

的正则化项是K棵树的正则化项相加而来的。

上图为第K棵CART树，确定?棵CART树需要确定两部分， 第?部分就是树的结构，这个结构将

输?样本映射到?个确定的叶子节点上，记为f (x); 第?部分就是各个叶子节点的值，q(x)表示输出

的叶子节点序号，w (x)表示对应叶子节点序号的值。 由定义得：

XGBoost法对应的模型包含了多棵cart树，定义每棵树的复杂度：

其中T为叶子节点个数，||w||为叶子节点向量的模 。γ表示节点切分的难度，λ表示L2正则化系数。

2.1 目标函数推导

根据（3.1）式，共进行t次迭代的学习模型的目标函数为：

由前向分布算法可知，前t-1棵树的结构为常数：

我们知道，泰勒公式的?阶导近似表示：

令ft(xi)为Δx, 则（3.5）式的?阶近似展开：

因为为常数，所以

其中：gi 和hi 分别表示预测误差对当前模

型的?阶导和?阶导；表示前t-1棵树组成的学习模型的预测误差。 当前模型往预测误

差减小的方向进行迭代。 忽略（3.8）式常数项，并结合（3.4）式，得：

，通过（3.2）式简化（3.9）式：

（3.10）式第?部分是对所有

训练样本集进行累加， 此时，所有样本都是映射为树的叶子节点，所以，我们换种思维，从叶子

节点出发，对所有的叶子节点进行累加，得：

令，Gj 表示映射为叶子节点 j 的所有输?样本的?阶导之和，同理，H 表示

?阶导之和。 得：

对于第 t 棵CART树的某?个确定结构（可用q(x)表示），其叶子节点是相互独立的， G 和H 是确

定量，因此，（3.12）可以看成是关于叶子节点w的?元?次函数 。 最小化（3.12）式，得：

，把（3.13）带?到（3.12），得到最终的目标函数：

，（3.14）也称为打分函数(scoring function)，它是衡量树结构

好坏的标准， 值越小，代表结构越好 。 我们用打分函数选择最佳切分点，从而构建CART树。

3. XGBoost的回归树构建方法

在实际训练过程中，当建立第 t 棵树时，XGBoost采用贪心法进行树结点的分裂：从树深为0时开

始：对树中的每个叶子结点尝试进行分裂； 每次分裂后，原来的?个叶子结点继续分裂为左右两

个子叶子结点，原叶子结点中的样本集将根据该结点的判断规则分散到左右两个叶子结点中；新分

裂?个结点后，我们需要检测这次分裂是否会给损失函数带来增益，增益的定义如下：

，如果增益Gain>0，即分裂为两个叶子节点后，目标函

数下降了，那么我们会考虑此次分裂的结果。那么?直这样分裂，什么时候才会停止呢？

3.1?停止分裂条件判断

情况?：上节推导得到的打分函数是衡量树结构好坏的标准，因此，可用打分函数来选择最佳切分

点。首先确定样本特征的所有切分点，对每?个确定的切分点进行切分，切分好坏的标准如下：

Gain表示单节点obj与切分后的两个节点的树obj之差， 遍历所有特征的切分点，找到最大Gain的

切分点即是最佳分裂点，根据这种方法继续切分节点，得到CART树。 若 γ 值设置的过大，则

Gain为负，表示不切分该节点，因为切分后的树结构变差了。 γ 值越大，表示对切分后obj下降幅

度要求越严，这个值可以在XGBoost中设定。 情况?：当树达到最大深度时，停止建树，因为树

的深度太深容易出现过拟合，这?需要设置?个超参数max_depth。 情况三：当引入?次分裂

后，重新计算新生成的左、右两个叶子结点的样本权重和。如果任?个叶子结点的样本权重低于某

?个阈值，也会放弃此次分裂。这涉及到?个超参数：最小样本权重和，是指如果?个叶子节点包

含的样本数量太少也会放弃分裂，防止树分的太细，这也是过拟合的?种措施。?

XGBoost与GDBT的区别：①XGBoost?成CART树考虑了树的复杂度，GDBT未考虑，GDBT在树

的剪枝步骤中考虑了树的复杂度。 ②XGBoost是拟合上?轮损失函数的?阶导展开，GDBT是拟合

上?轮损失函数的?阶导展开，因此，XGBoost 的准确性更高，且满足相同的训练效果，需要的

迭代次数更少。 ③XGBoost与GDBT都是逐次迭代来提高模型性能，但是XGBoost在选取最佳切分

点时可以开启多线程进行，大大提高了运行速度。

4.?xgboost算法api介绍

官?链接：https://xgboost.readthedocs.io/en/latest/

pip3 install xgboost

xgboost中封装了很多参数，主要由三种类型构成：通用参数（general parameters），Booster 参

数（booster parameters）和学习目标参数（task parameters），通用参数：主要是宏观函数控

制； Booster参数：取决于选择的Booster类型，用于控制每?步的booster（tree, regressiong）；

学习目标参数：控制训练，目标的表现。

通用参数（general parameters）：

1. booster [缺省值=gbtree]

2. 决定使用哪个booster，可以是gbtree，gblinear或者dart。 gbtree和dart使用基于树的模型(dart

主要多了 Dropout)，而gblinear 使用线性函数。

3. silent [缺省值=0] 设置为0打印运行信息；设置为1静默模式，不打印

4. nthread [缺省值=设置为最大可能的线程数] 并行运行xgboost的线程数，输?的参数应该<=系统

的CPU核心数，若是没有设置算法会检测将其设置为CPU 的全部核心数

下面的两个参数不需要设置，使用默认的就好了：

1. num_pbuffer [xgboost自动设置，不需要用户设置] 预测结果缓存大小，通常设置为训练实例的

个数。该缓存用于保存最后boosting操作的预测结果。

2. num_feature [xgboost自动设置，不需要用户设置] 在boosting中使用特征的维度，设置为特征的

最大维度

Booster 参数（booster parameters）：

1. eta [缺省值=0.3，别名：learning_rate] 更新中减少的步长来防止过拟合。 在每次boosting之

后，可以直接获得新的特征权值，这样可以使得boosting更加鲁棒。 范围：[0,1]

2. gamma [缺省值=0，别名: min_split_loss]（分裂最小loss） 在节点分裂时，只有分裂后损失函

数的值下降了，才会分裂这个节点。 Gamma指定了节点分裂所需的最小损失函数下降值。 这个参

数的值越大，算法越保守。这个参数的值和损失函数息息相关，所以是需要调整的。 范围: [0,∞]

3. max_depth [缺省值=6] 这个值为树的最大深度。 这个值也是用来避免过拟合的。max_depth越

大，模型会学到更具体更局部的样本。 设置为0代表没有限制范围: [0,∞]

4. min_child_weight [缺省值=1] 决定最小叶子节点样本权重和。XGBoost的这个参数是最小样本权

重的和。当它的值较大时，可以避免模型学习到局部的特殊样本。 但是如果这个值过高，会导致

欠拟合。这个参数需要使用CV来调整。范围: [0,∞]

5. subsample [缺省值=1] 这个参数控制对于每棵树，随机采样的比例。 减小这个参数的值，算法

会更加保守，避免过拟合。但是，如果这个值设置得过小，它可能会导致欠拟合。典型值：0.5-

1，0.5代表平均采样，防止过拟合。范围: (0,1]

6. colsample_bytree [缺省值=1] 用来控制每棵随机采样的列数的占比(每?列是?个特征)。 典型

值：0.5-1 范围: (0,1]

7. colsample_bylevel [缺省值=1] 用来控制树的每?级的每?次分裂，对列数的采样的占比。 我个

??般不太用这个参数，因为subsample参数和colsample_bytree参数可以起到相同的作用。但是

如果感兴趣，可以挖掘这个参数更多的用处。 范围: (0,1]

8. lambda [缺省值=1，别名: reg_lambda] 权重的L2正则化项(和Ridge regression类似)。 这个参数

是用来控制XGBoost的正则化部分的。虽然大部分数据科学家很少用到这个参数，但是这个参数

在减少过拟合上还是可以挖掘出更多用处的。

9. alpha [缺省值=0，别名: reg_alpha] 权重的L1正则化项。(和Lasso regression类似)。 可以应用

在很高维度的情况下，使得算法的速度更快。

10. scale_pos_weight[缺省值=1] 在各类别样本十分不平衡时，把这个参数设定为?个正值，可以

使算法更快收敛。通常可以将其设置为负样本的数目与正样本数目的比值。

11. lambda [缺省值=0，别称: reg_lambda] L2正则化惩罚系数，增加该值会使得模型更加保守。

12. alpha [缺省值=0，别称: reg_alpha] L1正则化惩罚系数，增加该值会使得模型更加保守。

13. lambda_bias [缺省值=0，别称: reg_lambda_bias] 偏置上的L2正则化(没有在L1上加偏置，因

为并不重要)

学习目标参数（task parameters）：

1. objective [缺省值=reg:linear] i. “reg:linear” – 线性回归 ii. “reg:logistic” – 逻辑回归 iii.

“binary:logistic” – ?分类逻辑回归，输出为概率 iv. “multi:softmax” – 使?softmax的多分类器，返

回预测的类别(不是概率)。在这种情况下，你还需要多设?个参数：num_class(类别数目) v.

“multi:softprob” – 和multi:softmax参数?样，但是返回的是每个数据属于各个类别的概率。

2. eval_metric [缺省值=通过目标函数选择] 可供选择的如下所示： i. “rmse”: 均方根误差 ii. “mae”:

平均绝对值误差 iii. “logloss”: 负对数似然函数值 iv. “error”: ?分类错误率。 其值通过错误分类数目

与全部分类数目比值得到。对于预测，预测值大于0.5被认为是正类，其它归为负类。 v. “error@t”:

不同的划分阈值可以通过 ‘t’ 进行设置 vi. “merror”: 多分类错误率，计算公式为(wrong cases)/(all

cases) vii. “mlogloss”: 多分类log损失 viii. “auc”: 曲线下的面积

3. seed [缺省值=0] 随机数的种子，设置它可以复现随机数据的结果，也可以用于调整参数

5.?xgboost案例

案例：https://www.kaggle.com/c/titanic/overview

数据：http://biostat.mc.vanderbilt.edu/wiki/pub/Main/DataSets/titanic.txt

import pandas as pd
import numpy as np
from sklearn.feature_extraction import DictVectorizer
from sklearn.model_selection import train_test_split
# 1、获取数据
titan = pd.read_csv("http://biostat.mc.vanderbilt.edu/wiki/pub/Main/DataSets/titanic.txt")
x = titan[["pclass", "age", "sex"]]
y = titan["survived"]
# 缺失值需要处理，将特征当中有类别的这些特征进?字典特征抽取
x['age'].fillna(x['age'].mean(), inplace=True)
x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=22)
# 对于x转换成字典数据x.to_dict(orient="records")
# [{"pclass": "1st", "age": 29.00, "sex": "female"}, {}]
transfer = DictVectorizer(sparse=False)
x_train = transfer.fit_transform(x_train.to_dict(orient="records"))
x_test = transfer.fit_transform(x_test.to_dict(orient="records"))
# 模型初步训练
from xgboost import XGBClassifier
xg = XGBClassifier()
xg.fit(x_train, y_train)
xg.score(x_test, y_test)
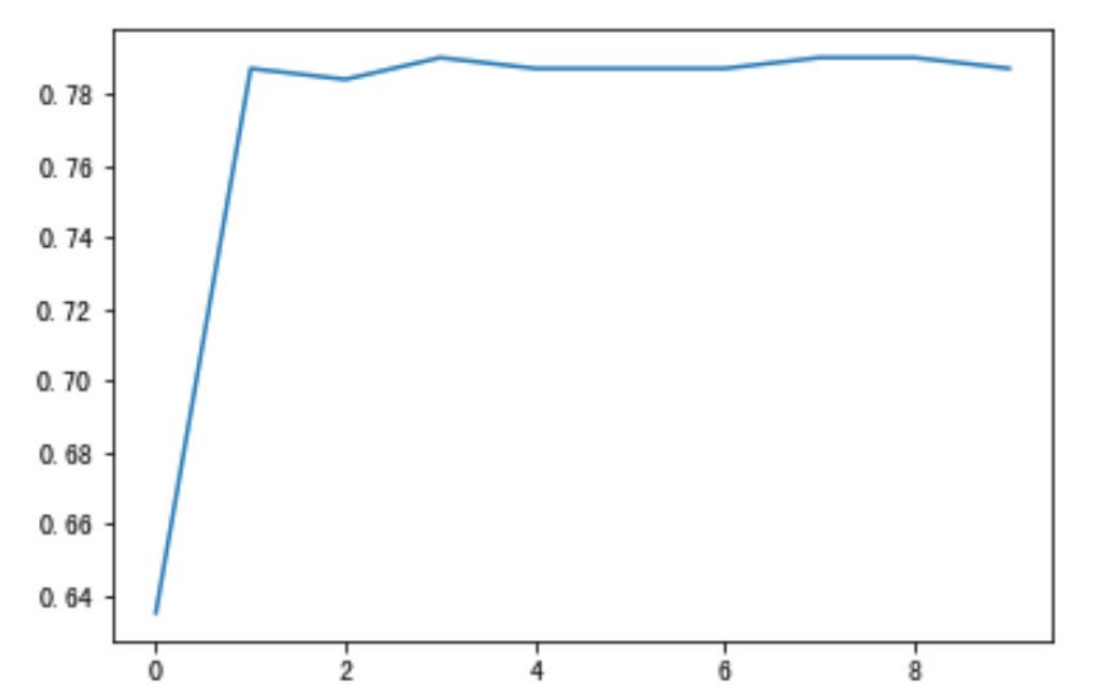
# 针对max_depth进?模型调优
depth_range = range(10)
score = []
for i in depth_range:
xg = XGBClassifier(eta=1, gamma=0, max_depth=i)
xg.fit(x_train, y_train)
s = xg.score(x_test, y_test)
print(s)
score.append(s)# 结果可视化
import matplotlib.pyplot as plt
plt.plot(depth_range, score)
plt.show()