代码随想录算法训练营第二十二天| 回溯 93.复原IP地址 78.子集 90.子集II

93. 复原 IP 地址

递归参数：index一定是需要的，记录下一层递归分割的起始位置。还需要一个变量pointNum，记录添加逗点的数量。

递归终止条件：明确要求只会分成4段，所以不能用切割线切到最后作为终止条件，而是分割的段数作为终止条件。pointNum表示逗点数量，pointNum为3说明字符串分成了4段了。然后验证一下第四段是否合法，如果合法就加入到结果集里

单层搜索的逻辑：在for (int i = startIndex; i < s.size(); i++)循环中 [startIndex, i] 这个区间就是截取的子串，需要判断这个子串是否合法。如果合法就在字符串后面加上符号.表示已经分割。如果不合法就结束本层循环，剪掉的分支。递归调用时，下一层递归的startIndex要从i+2开始（因为需要在字符串中加入了分隔符.），同时记录分割符的数量pointNum 要 +1。回溯的时候，就将刚刚加入的分隔符. 删掉就可以了，pointNum也要-1。

出现问题

1.直接进行简单的判断s[start]==0，并没有判断出现0时候的位置

2.区间定义出现问题，isBaild里面函数是左闭右闭区间，然而在调用函数时进去的是左闭右开区间

class Solution {
public:
    vector<string> res;
    bool isValid(string &s,int start,int end){
        if(start>end)return false;
        if(s[start]=='0'  && start != end)return false;
        int num=0;
        while(start<=end){
            if(s[start]<'0'||s[start]>'9')return false;
            num = num * 10 + (s[start] - '0');
            if(num>255)return false;
            start++;
        }
        return true;
    }

    void backtracing(string &s,int index,int pointnum){
       if(pointnum==3){
           if(isValid(s,index,s.size()-1)){
              res.push_back(s);
              return; 
           }  
       }
        for(int i=index;i<s.size();i++){
            if(isValid(s,index,i)){
                s.insert(s.begin() + i + 1 , '.');  // 在i的后面插入一个逗点
                pointnum++;
                backtracing(s, i + 2, pointnum);   // 插入逗点之后下一个子串的起始位置为i+2
                pointnum--;  
                s.erase(s.begin() + i + 1);                    
            }
        }


    }
    
    vector<string> restoreIpAddresses(string s) {
        res.clear();
        backtracing(s,0,0);
        return res;
    }
};

78. 子集

如果把 子集问题、组合问题、分割问题都抽象为一棵树的话，那么组合问题和分割问题都是收集树的叶子节点，而子集问题是找树的所有节点！

那么既然是无序，取过的元素不会重复取，写回溯算法的时候，for就要从index开始，而不是从0开始！

递归函数参数:全局变量数组path为子集收集元素，二维数组res存放子集组合。

递归终止条件:前面直接if(index<nums.size())，出现结果空集的情况，后面仔细一想，不用终止条件是不是也行

单层搜索逻辑：求取子集问题，不需要任何剪枝！因为子集就是要遍历整棵树。

class Solution {
public:
    vector<vector<int>> res;
    vector<int> path;

    void backtracking(vector<int> &nums, int index){
        res.push_back(path);
        for(int i=index;i<nums.size();i++){
            path.push_back(nums[i]);
           
            backtracking(nums,i+1);
            path.pop_back();
        }
    }


    vector<vector<int>> subsets(vector<int>& nums) {
        res.clear();
        path.clear();
        backtracking(nums,0);
        return res;
    }
};

90. 子集 II

?

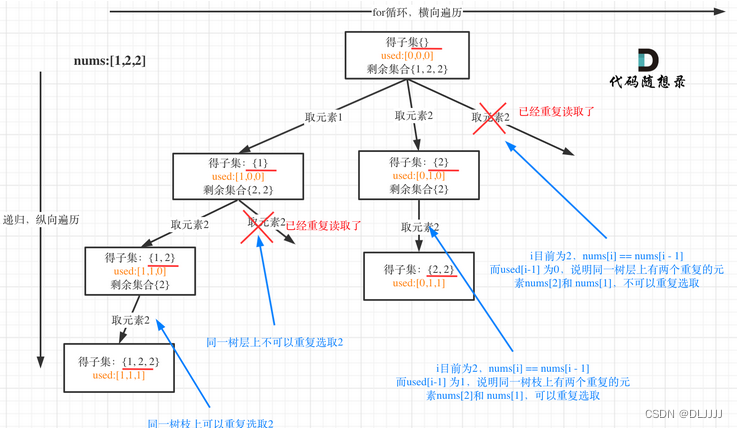
从图中可以看出，同一树层上重复取2 就要过滤掉，同一树枝上就可以重复取2，因为同一树枝上元素的集合才是唯一子集！?

递归函数参数:全局变量数组path为子集收集元素，二维数组res存放子集组合。需要一个used数组用于去重。

递归终止条件:子集问题可以不用写

单层搜索逻辑：求取子集问题，不需要任何剪枝！因为子集就是要遍历整棵树

class Solution {
public:
    vector<int> path;
    vector<vector<int>> res;
    void backtracking(vector<int>& nums, int index,vector<bool> used){
        res.push_back(path);
        for(int i=index;i<nums.size();i++){
            if(i>0&&nums[i]==nums[i-1]&&used[i-1]==false) continue;
            used[i]=true;
            path.push_back(nums[i]);
            backtracking(nums,i+1,used);
            used[i]=false;
            path.pop_back();
        }
    }

    vector<vector<int>> subsetsWithDup(vector<int>& nums) {
        vector<bool> used(nums.size(),false);
        path.clear();
        res.clear();
        sort(nums.begin(),nums.end());
        backtracking(nums,0,used);
        return res;
    }
};