OpenVINS学习3——初始化原理学习

一、OpenVINS初始化概述

VIO初始化的主要意义有：

（1）对齐相机的世界坐标系和惯性系，因此需要估计重力方向。

（2）为后续的VIO算法提供较为准确的初始参数和状态（尺度、IMU bias、初始速度）,使得算法可以快速稳定地进入正常运行阶段。

良好的初始化对VIO算法的整体精度和鲁棒性至关重要。

目前OpenVINS包含视觉惯性系统的 StaticInitializer 和 DynamicInitializer 初始化代码。它将等待平台静止，然后初始化其在重力框架中的方向。

一般VIO初始化分为两种，一种是静态初始化，一种是动态初始化，而OpenVins则利用加速度的方差差异将运动分为两种状态，一种是静止的，一种是刚开始运动的。

VIO初始化就要任务一般是估计重力方向，速度，位置，IMU的偏置，尺度。而在openvins中，只估计重力方向，IMU的偏置。

在代码里主要写了三个初始化模式：

1) GroundTruth初始化

2 )静止初始化

3 )动态初始化

关于静止初始化，可以参考不一样的静态初始化——OpenVins-CSDN博客

静止初始化 - 知乎

如果平台初始时不是静止的，那么我们利用动态初始化来尝试恢复初始状态。这是Estimator Initialization in Vision-aided Inertial Navigation with Unknown Camera-IMU Calibration的实现，它通过首先创建一个用于恢复速度、重力和特征位置的线性系统来解决初始化问题。初始恢复后，执行全面优化以允许协方差恢复。

Estimator Initialization in Vision-aided Inertial Navigation with Unknown Camera-IMU Calibration论文阅读博客：

论文阅读Estimator Initialization in Vision-aided Inertial Navigation with Unknown Camera-IMU Calibration-CSDN博客

二、静态初始化原理

静止初始化 - 知乎在VIO/VINS系统中，初始化是指在系统启动阶段，需要估计(设置) 重力方向(gravity direction)、初始速度(initial velocity)、初始位置(initial position)、加速度计以及陀螺仪biases (accelerometer and gyroscope …https://zhuanlan.zhihu.com/p/282875390

三、动态初始化原理

视觉惯性导航系统( VINS )的一个基本问题是其状态初始化。也就是说，恢复给定惯性和视觉方位测量的初始可观测状态。众所周知，VINS具有4个自由度的不可观测方向，对应于全局的偏航和位置[ 1 ]。这意味着其他参数是可观测的，因此，在给定惯性和视觉测量读数的情况下，它们是可恢复的。状态初始化的挑战是在没有任何先验知识的情况下，通过构造一个线性系统来恢复这些可观测参数。这并不简单，因为定向是非线性的，因此如果没有近似和技巧，很难定义这样的线性问题。接下来，在Dong - Si和穆里基斯工作的基础上，给出了问题的闭式解，并定义了一个二次约束最小二乘问题[ 2、3]。另外一个重点是，希望恢复初始状态协方差，以便用于基于滤波器的视觉惯性扩展卡尔曼滤波器OpenVINS [ 4 ]。

1、最小二乘方程构建

利用IMU模型和相机模型，从相机归一化平面的坐标等式出发，利用IMU提供的姿态信息，以特征点全局位置、IMU速度、重力加速度为因变量，列出形如Ax=b的方程。

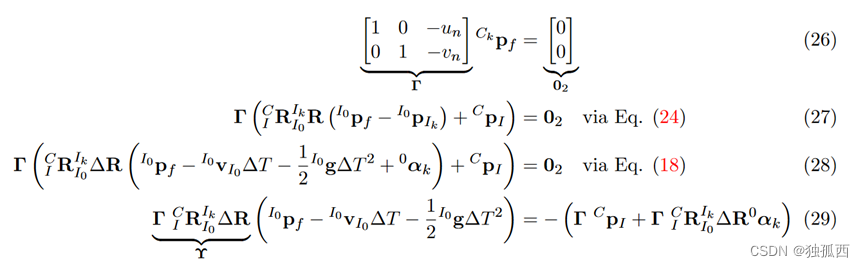
如果有五个以上的框架，就可以恢复上述的线性系统(即当N = 5时, 2N≥9 )。如果重力被限制在一个已知的量级，那么这就减少了自由度，因此只需要四个观测值(即当N = 4时,满足2N≥8)就可以恢复状态。这与[ 2、3]中的结果不同，因为没有尝试将相机外参恢复到IMU变换中。该系统可以对所有特征观测值进行叠加，同时增加了系统的鲁棒性。

加上重力加速度的约束，再利用拉格朗日乘子法，得到新的无约束问题，对该多项式的伴随矩阵进行特征分解，可以找到该多项式的根(从而解得)。

恰好满足约束的最小λ解将给出最优解：

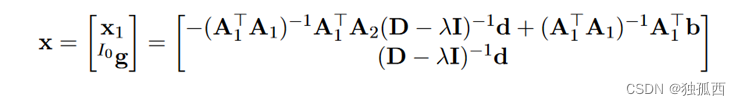
现在希望恢复每个相机时间步的惯性状态，这将作为下一部分非线性优化的初始猜测。利用惯性传播，可以恢复每个时刻的惯性状态：

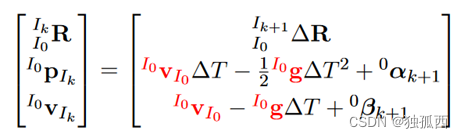
用红色突出了从约束最小二乘中恢复的分量和?T从t0时刻到tk时刻。现在希望将第一参照系与引力参照系对齐。这意味着将计算一个框架{ G }，使得重力为Gg = [ 0 0 ?9 . 81] ，其位置和偏航在{ I0 }原点。利用施密特正交方法把全局坐标系和惯性坐标系进行对齐。可以发现其z轴沿重力方向的旋转为：

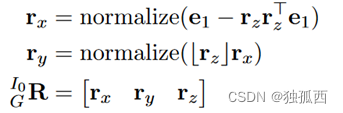
至此，初始化估计重力方向这个问题解决。

2、精细化

利用线性系统，我们恢复了状态的一个初始猜测。在此，希望对估计值进行精化，使其更接近真实值，并恢复初始状态的协方差。这个过程还将考虑到系统的噪声特性，使得每个测量相对于其传感器的精度是加权的。可以定义下面希望优化的状态

其中在每个成像时间步都有C个惯性状态，和N个环境特征。可以定义如下带有惯性，相机和先验因子的优化问题：

?

四、代码解析

OpenVINS的初始化代码在ov_init文件夹下，主要分为静态初始化和动态初始化两部分。下一个博客重点写一下初始化代码得到结构功能，写一个详尽的注释。