【数学建模】智能算法
智能算法,也称现代优化算法
模拟退火算法
简介
材料统计力学观点:材料中粒子的不同结构对应于粒子的不同能量水平
在高温条件下,粒子的能量较高,可以自由运动和重新排列。在低温条件下,粒子能量较低。如果从高温开始,非常缓慢地降温(这个过程被称为退火),粒子就可以在每个温度下达到热平衡,最终形成处于低能状态的晶体。
用粒子的能量定义材料的状态,假设材料在状态
i
i
i之下的能量为
E
(
i
)
E(i)
E(i),则在温度
T
T
T时,材料从状态
i
i
i转换为状态
j
j
j满足:
(1)如果
E
(
j
)
≤
E
(
i
)
E({j})\leq E({i})
E(j)≤E(i) ,接受该状态被转换。
(2)如果
E
(
j
)
>
E
(
i
)
E(j)>E(i)
E(j)>E(i) ,则状态转换以如下概率被接受
e
E
(
i
)
?
E
(
j
)
K
T
e^{{\frac{E\left(i\right)-E\left(j\right)}{K T}}}
eKTE(i)?E(j)?
说明:
K
\textstyle{K}
K 是物理学中的波尔兹曼常数,
T
{\textstyle{T}}
T是材料温度
数学基础
-
当处在一个特定的温度下时,材料进行了充分的转换达到了热平衡,这时材料处于状态 i i i的概率满足波尔兹曼分布
P T ( X = i ) = e ? E ( i ) K T ∑ j ∈ S e ? E ( j ) K T P_{T}(X=i)=\frac{e^{-\frac{E(i)}{K T}}}{\displaystyle\sum_{j\in S}e^{-\frac{E(j)}{K T}}} PT?(X=i)=j∈S∑?e?KTE(j)?e?KTE(i)??
说明: X \boldsymbol{X} X 表示材料当前状态的随机变量, S {\mathsf{S}} S 表示状态空间集合
lim ? T → ∞ e ? F ( i ) k T ∑ j ∈ S e ? F ( j ) k T = 1 ∣ S ∣ \lim_{T \to \infty} \frac{e^{-\frac{F(i)}{k T}}}{\sum_{j\in S} e^{-\frac{F(j)}{k T}}} = \frac{1}{|S|} T→∞lim?∑j∈S?e?kTF(j)?e?kTF(i)??=∣S∣1?
说明:这代表所有状态在高温下具有相同的概率 -
当温度开始下降时
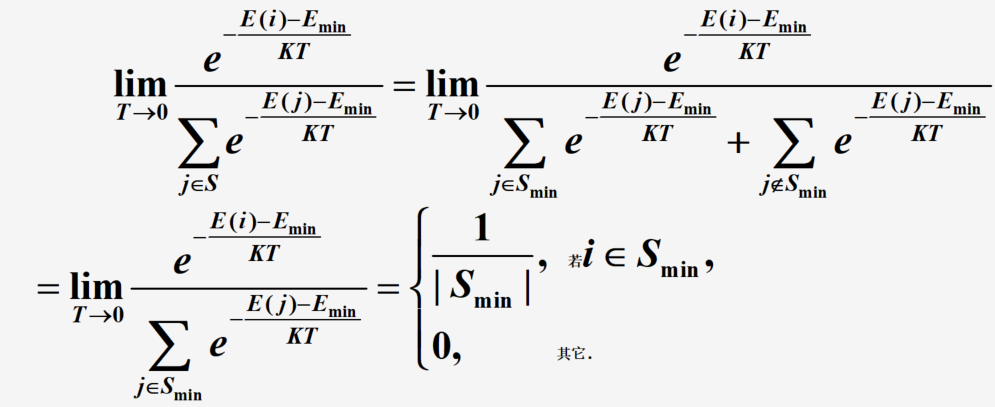
说明: E m i n = m i n j ∈ S E ( j ) E_{\mathrm {min}}=\mathrm{min_{j \in S}}E(j) Emin?=minj∈S?E(j)且 S m i n = { i ∣ E ( i ) = E m i n } S_{\mathrm{min}}=\left\{i\mid{E}(i)={E}_{\mathrm{min}}\right\} Smin?={i∣E(i)=Emin?}
如果温度下降十分缓慢,而在每个温度都有足够多次的状态转移,使之在每一个温度下达到热平衡,则全局最优解将以概率1被找到。模拟退火算法的正确性得以验证。
注意事项
- 降温速度的选取需要在解的性能和算法速度之间取一个tradeoff
- 需要确定在每个温度下状态转换的结束准则,比如设定为连续 m m m次的转换过程中没有使状态发生变化就结束该温度下的状态转换过程。
- 需要确定退火最终温度。比如提前设定一个较小的 T T T。比如连续几个温度下转换过程没有使状态发生变化就结束
- 选择合适的初始温度和某个可行解的邻域方法需要恰当
算法流程及应用
算法流程
模拟退火算法分为两个过程:Metropolis采样过程和退火实现过程
Metropolis采样过程
输入当前解s和温度
T
{\mathcal{T}}
T :
(1)令
k
=
0
k =0
k=0 时的当前解为
s
(
0
)
=
s
s(0)=s
s(0)=s ,而在温度
T
T
T 下进行以下步骤
(2)按某一规定方式根据当前解
s
(
k
)
s(k)
s(k)所处的状态
s
s
s,产生一个邻近子集
N
(
s
(
k
)
)
N(s(k))
N(s(k)) ,由
N
(
s
(
k
)
)
N(s(k))
N(s(k)) 随机产生一个新的状态
s
′
s'
s′作为一个候选解,取评价函数
C
(
?
)
{\mathbf{}}C(\cdot)
C(?) ,计算
Δ
C
′
=
C
(
s
′
)
?
C
(
s
(
k
)
)
.
\Delta C^{\prime}=C(s^{\prime})-C(s(k)).
ΔC′=C(s′)?C(s(k)).
(3)若
Δ
C
′
≤
0
\Delta C^{\prime}\leq 0
ΔC′≤0,则接受
s
′
s'
s′作为下一个当前解,若
Δ
C
′
>
0
\Delta C^{\prime}>0
ΔC′>0,则按概率
e
?
Δ
C
′
T
e^{-\frac{\Delta{C^{\prime}}}{T}}
e?TΔC′?接受
s
′
s'
s′作为下一个当前解
(4)若接受s’,则令
s
(
k
+
1
)
=
s
s(k+1)=s
s(k+1)=s ',否则令
s
(
k
+
1
)
=
s
(
k
)
s(k+1)=s(k)
s(k+1)=s(k)
(5)令
k
=
k
+
1
k=k+1
k=k+1 ,判断是否满足收敛准则,不满足则转移到(2);否则转步骤(6)
(6)返回当前解s(k)
退火实现过程
(1)任选一初始状态
s
0
s_{0}
s0? 作为初始解
s
(
0
)
=
s
0
s(0)=s_{0}
s(0)=s0? ,并设初值温度为
T
0
T_0
T0?,令
i
=
0
i=0
i=0
(2)以
T
i
\textstyle T_{i}
Ti? 和
s
i
s_{i}
si? 调用 Metropolis 采样算法,然后返回当前解
s
i
=
s
s_{i}=s
si?=s
(3)按一定方式将
T
T
T降温,令
i
=
i
+
1
{\mathit{i}}={\mathit{i}}+1
i=i+1 ,
T
i
=
T
i
+
Δ
T
(
Δ
T
<
0
)
T_{i}=T_{i}+\Delta T(\Delta T<0)
Ti?=Ti?+ΔT(ΔT<0) 。
(4)检查退火过程是否结束,若未结束则转移到(2);否则转(5)
(5)以当前解
s
i
s_{i}
si? 作为最优解输出
算法应用


问题说明
这是一个旅行商问题。
给我方基地编号为 0,目标依次编号为1,2,…, 100,最后我方基地再重复编号为 101。距离矩阵
D
=
(
d
i
j
)
102
×
102
D=(d_{i j})_{102\times102}
D=(dij?)102×102? ,其中
d
i
j
d_{ij}
dij?表示表示i,j两点的距离,i,j = 0,1,…,101,这里D为实对称矩阵
问题抽象为求从点0出发,走遍所有中间点,到达点 101的一个最短路径
- 距离求解
将题目中的经纬度坐标转化为两点之间的实际距离
设 A A A、 B B B两点的大地坐标为 ( x 1 , y 1 ) (x_1, y_1) (x1?,y1?), ( x 2 , y 2 ) (x_2, y_2) (x2?,y2?)(其中 x 1 , x 2 x_1, x_2 x1?,x2?为经度, y 1 , y 2 y_1, y_2 y1?,y2?为纬度),则两点之间的实际距离为过 A A A、 B B B两点的大圆的劣弧长
以地心为坐标原点 O O O,以以赤道平面为 X O Y XOY XOY 平面,以零度经线圈所在的平面为 X O Z XOZ XOZ平面建立三维直角坐标系,则 A A A、 B B B两点的直角坐标为
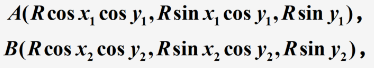
其中 R R R=6370km为地球半径
A , B A,B A,B 两点的实际距离:
d
=
R
arccos
?
(
O
A
?
?
O
B
?
∣
∣
O
A
?
∣
2
∣
∣
O
B
?
∣
)
d=R\arccos\left(\frac{\vec{OA}\cdot\vec{O B}}{\displaystyle|\displaystyle|\vec{OA}|^{2}\left|\displaystyle|\vec{OB}\right|}\right)
d=Rarccos
?∣∣OA∣2
?∣OB
?OA?OB?
?
化简得
d = R arccos ? [ cos ? ( x 1 ? x 2 ) cos ? y 1 cos ? y 2 + sin ? y 1 sin ? y 2 ] . d=R\operatorname{arccos}[\cos(x_{1}-x_{2})\cos y_{1}\cos y_{2}+\sin y_{1}\sin y_{2}]. d=Rarccos[cos(x1??x2?)cosy1?cosy2?+siny1?siny2?].
- 模型及算法
(1)解空间:
解空间S可表为{0,1,…,101}的所有固定起点和终点的循环排列集合, 即
S = { ( π 0 , π 1 , ? ? , π 101 ) ? ∣ ? π 0 = 1 , ( π 1 , π 2 , ? ? , π 100 ) 为 { 1 , 2 , ? ? , 100 } 的循环排列 , π 101 = 101 } S=\{(\pi_0,\pi_{1},\cdots,\pi_{101})\,|\,\pi_0=1,(\pi_{1},\pi_{2},\cdots,\pi_{100})为\{1,2,\cdots,100\}的循环排列,\pi_{101}=101\} S={(π0?,π1?,?,π101?)∣π0?=1,(π1?,π2?,?,π100?)为{1,2,?,100}的循环排列,π101?=101}
其中每一个循环排列表示侦察 100 个目标的一个回路, π i = j \pi_{i}=j πi?=j 表示在第i次侦察目标
初始解可选为(0,1,··,101),本文中我们先使用 Monte Carlo(蒙特卡洛)方法求得一个较好的初始解
(2)目标函数:侦察所有目标的路径长度
m i n ? f ( π o , π 1 , ? ? , π i n t ) = ∑ i = 0 100 d π i π i + 1 \mathrm{min}\,f(\pi_{\mathrm{o}},\pi_{1},\cdots,\pi_{\mathrm{int}})=\sum_{i=0}^{100}d_{\pi_{i}\pi_{i+1}} minf(πo?,π1?,?,πint?)=i=0∑100?dπi?πi+1??
(3)新解的产生

(4)接受准则
P = { 1 , Δ f < 0 , exp ? ( ? Δ f ? / T ) , Δ f ≥ 0. P=\left\{\begin{array}{l l}{{1,}}&{{\Delta f<0,}}\\ {{\exp(-\Delta f\ /T),}}&{{\Delta f\geq0.}}\end{array}\right. P={1,exp(?Δf?/T),?Δf<0,Δf≥0.?
说明:若 Δ f < 0 \Delta f<0 Δf<0,则接受新的路径;否则,以概率 exp ? ( ? Δ f ? / T ) \exp(-\Delta f\ /T) exp(?Δf?/T)接受新的路径,具体操作为产生一个一个 [ 0 , 1 ] [0,1] [0,1]区间上均匀分布的随机数 rand,若rand ≤ exp ? ( ? Δ f ? / T ) \leq\exp(-\Delta f\ /T) ≤exp(?Δf?/T) 则接受
(5)降温
利用选定的降温系数 α \alpha α进行降温,取新的温度 T T T为 α T \alpha T αT(这里 T T T为上一步迭代的温度),这里选定 α = 0.999 \alpha=0.999 α=0.999
(6)结束条件
用选定的终止温度 e = 1 0 ? 30 e=10^{-30} e=10?30,判断退火过程是否结束。若 T < e \textstyle T<e T<e ,算法结束,输出当前状态
模型求解
from numpy import loadtxt,radians,sin,cos,inf,exp
from numpy import array,r_,c_,arange,savetxt
from numpy.lib.scimath import arccos
from numpy.random import shuffle,randint,rand
from matplotlib.pyplot import plot, show, rc
a=loadtxt("Pdata17_1.txt")
x=a[:,::2]. flatten(); y=a[:,1::2]. flatten()
d1=array([[70,40]]); xy=c_[x,y]
xy=r_[d1,xy,d1]; N=xy.shape[0]
t=radians(xy) #转化为弧度
d=array([[6370*arccos(cos(t[i,0]-t[j,0])*cos(t[i,1])*cos(t[j,1])+
sin(t[i,1])*sin(t[j,1])) for i in range(N)]
for j in range(N)]).real
savetxt('Pdata17_2.txt',c_[xy,d]) #把数据保存到文本文件,供下面使用
path=arange(N); L=inf
for j in range(1000):
path0=arange(1,N-1); shuffle(path0)
path0=r_[0,path0,N-1]; L0=d[0,path0[1]] #初始化
for i in range(1,N-1):L0+=d[path0[i],path0[i+1]]
if L0<L: path=path0; L=L0
print(path,'\n',L)
e=0.1**30; M=20000; at=0.999; T=1
for k in range(M):
c=randint(1,101,2); c.sort()
c1=c[0]; c2=c[1]
df=d[path[c1-1],path[c2]]+d[path[c1],path[c2+1]]-\
d[path[c1-1],path[c1]]-d[path[c2],path[c2+1]] #续行
if df<0:
path=r_[path[0],path[1:c1],path[c2:c1-1:-1],path[c2+1:102]]; L=L+df
else:
if exp(-df/T)>=rand(1):
path=r_[path[0],path[1:c1],path[c2:c1-1:-1],path[c2+1:102]]
L=L+df
T=T*at
if T<e: break
print(path,'\n',L) #输出巡航路径及路径长度
xx=xy[path,0]; yy=xy[path,1]; rc('font',size=16)
plot(xx,yy,'-*'); show() #画巡航路径
遗传算法
Genetic Algorithem, GA,是模拟达尔文的遗传选择和自然淘汰的生物进化过程的计算模型
全局优化搜索算法
基本思想
基因代表问题的参数,问题的解代表染色体,从而得到一个由具有不同染色体的个体组成的群体。
拥有不同染色体的个体即为问题的一个不同的解。包含代表不同解的个体的群体在问题环境中生存竞争,好的解会有更好的机会生存繁殖,在整个过程中实现群体中的染色体都逐渐适应环境,不断进化,最后收敛到一族最适应环境的类似个体,即得到问题最优解。
遗传算法的原理
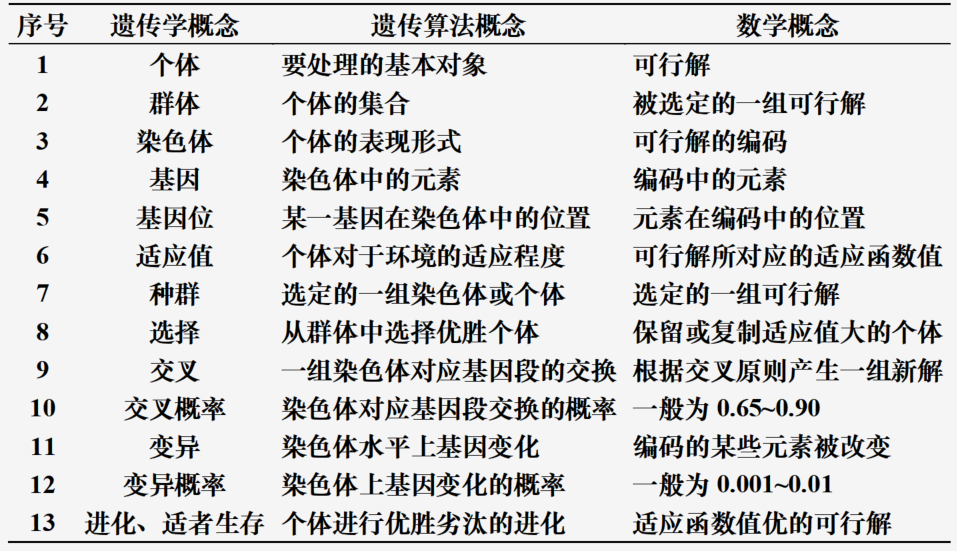
生物遗传学概念
遗传学概念、遗传算法概念和数学概念三者之间的对应关系如下图所示
遗传算法的步骤
三个基本操作(或称为算子):选择(Selection)、交叉(Crossover)、变异(Mutation)
(1)把问题的解表示成“染色体”,以二进制或十进制编码的串,在执行遗传算法之前,给出一群“染色体”,也就是假设的可行解
(2)把这些假设的可行解置于问题的“环境”中,并按适者生存的原则,选择出较适应环境的“染色体”进行复制,再通过交叉、变异过程产生更适应环境的新一代“染色体”群
(3)最后收敛到最适应环境的一个“染色体”上,它就是问题的最优解
具体步骤如下:
- 选择编码策略,把可行解集合转换为染色体结构空间
- 定义适应函数,便于计算适应值
- 确定遗传策略,包括选择群体大小、选择、交叉、变异方向以及确定交叉概率、变异概率等遗传参数
- 随机或用某种特殊方法产生初始化群体
- 按照遗传策略,运用选择、交叉和变异算子作用于群体,根据适应函数值,选择形成下一代群体
- 判断群体性能是否满足某一指标,或者是否已经完成预定的迭代次数,不满足则返回第五步
遗传算法应用
使用遗传算法解决前面的飞机巡航问题
模型及算法
参数设定:
种群大小
M
=
50
M=50
M=50 ;最大代数
G
=
10
G=10
G=10 ;交叉率
p
c
=
1
p_c=1
pc?=1,交叉概率为1能保证种群的充分进化;变异率
p
m
=
0.1
p_{m}=0.1
pm?=0.1 ,一般而言,变异发生的可能性较小
编码策略:
采用十进制编码,用随机序列
ω
0
,
ω
1
,
?
?
,
ω
101
\omega_{\mathrm{0}},\omega_{\mathrm{1}},\cdots,\omega_{\mathrm{101}}
ω0?,ω1?,?,ω101? 作为染色体,其中
0
<
ω
i
<
1
0<\omega_{i}<1
0<ωi?<1 (i = 1,2,… ,100 ),
ω
0
=
0
\scriptstyle\omega_{0}=0
ω0?=0 ,
ω
101
=
1
\omega_{\mathrm{101}}=1
ω101?=1
每一个随机序列都和种群中的一个个体相对应
编码位置i代表目标i,位置i的随机数表示目标i在巡回中的顺序
初始种群:

目标函数:
目标函数为侦察所有目标的路径长度,适应度函数就取为目标函数
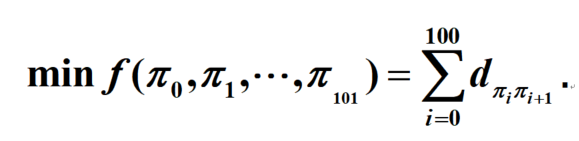
交叉操作:
使用单点交叉
设计如下,对于选定的两个父代个体
f
1
=
ω
o
ω
1
…
ω
101
?
,
??
f
2
=
ω
0
′
ω
1
′
…
ω
101
′
f_{1}=\omega_{\mathrm{o}}\omega_{\mathrm{1}}\ldots\omega_{\mathrm{101}}\,,~~f_{2}=\omega_{\mathrm{0}}^{\prime}\omega_{\mathrm{1}}^{\prime}\ldots\omega_{\mathrm{101}}^{\prime}
f1?=ωo?ω1?…ω101?,??f2?=ω0′?ω1′?…ω101′? ,随机地选取第t个基因处为交叉点, 则经过交叉运算后得到的子代个体为
s
1
s_1
s1?和
s
2
s_2
s2?,
s
1
s_1
s1?的基因由
f
1
f_1
f1?的前t个基因和
f
2
f_2
f2?的后102-t个基因构成,
s
2
s_2
s2?的基因由
f
2
f_2
f2?的前t个基因和
f
1
f_1
f1?的后102-t个基因构成
变异操作:
按照给定的变异率,对选定变异的个体,随机地取三个整数,满足
1
≤
u
<
ν
<
w
≤
100
1\leq u<\nu<w\leq100
1≤u<ν<w≤100 ,把u,v之间(包括u和v)的基因段插到w后面。
选择:
在父代种群和子代种群中选择目标函数值最小的
M
M
M个个体进化到下一代
模型求解
import numpy as np
from numpy.random import randint, rand, shuffle
from matplotlib.pyplot import plot, show, rc
a=np.loadtxt("Pdata17_2.txt")
xy,d=a[:,:2],a[:,2:]; N=len(xy)
w=50; g=10 #w为种群的个数,g为进化的代数
J=[];
for i in np.arange(w):
c=np.arange(1,N-1); shuffle(c)
c1=np.r_[0,c,101]; flag=1
while flag>0:
flag=0
for m in np.arange(1,N-3):
for n in np.arange(m+1,N-2):
if d[c1[m],c1[n]]+d[c1[m+1],c1[n+1]]<\
d[c1[m],c1[m+1]]+d[c1[n],c1[n+1]]:
c1[m+1:n+1]=c1[n:m:-1]; flag=1
c1[c1]=np.arange(N); J.append(c1)
J=np.array(J)/(N-1)
for k in np.arange(g):
A=J.copy()
c1=np.arange(w); shuffle(c1) #交叉操作的染色体配对组
c2=randint(2,100,w) #交叉点的数据
for i in np.arange(0,w,2):
temp=A[c1[i],c2[i]:N-1] #保存中间变量
A[c1[i],c2[i]:N-1]=A[c1[i+1],c2[i]:N-1]
A[c1[i+1],c2[i]:N-1]=temp
B=A.copy()
by=[] #初始化变异染色体的序号
while len(by)<1: by=np.where(rand(w)<0.1)
by=by[0]; B=B[by,:]
G=np.r_[J,A,B]
ind=np.argsort(G,axis=1) #把染色体翻译成0,1,…,101
NN=G.shape[0]; L=np.zeros(NN)
for j in np.arange(NN):
for i in np.arange(101):
L[j]=L[j]+d[ind[j,i],ind[j,i+1]]
ind2=np.argsort(L)
J=G[ind2,:]
path=ind[ind2[0],:]; zL=L[ind2[0]]
xx=xy[path,0]; yy=xy[path,1]; rc('font',size=16)
plot(xx,yy,'-*'); show() #画巡航路径
print("所求的巡航路径长度为:",zL)
人工神经网络
概述
artificial neural network, ANN
人工神经元
图示:
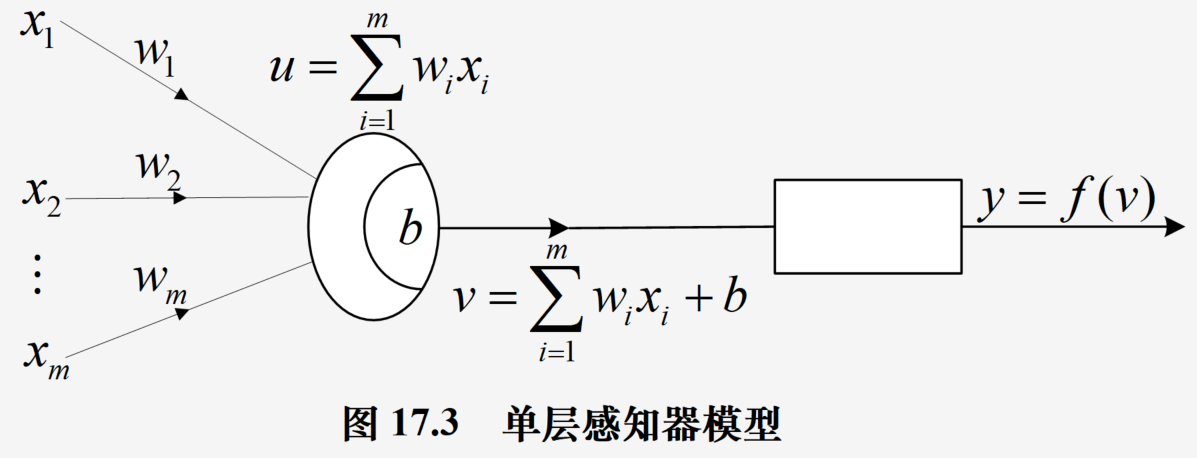
X
=
[
x
1
,
x
2
,
.
.
.
,
x
m
]
T
X=[x_1, x_2,..., x_m]^T
X=[x1?,x2?,...,xm?]T,
W
=
[
w
1
,
w
2
,
.
.
.
,
w
m
]
T
W=[w_1, w_2, ..., w_m]^T
W=[w1?,w2?,...,wm?]T为连接权
网络输入
u
=
∑
i
=
1
m
w
i
x
i
u=\sum^m_{i=1}w_ix_i
u=∑i=1m?wi?xi?,向量形式为
u
=
W
T
X
u=W^TX
u=WTX
激活函数
变换神经元获得的网络输入 u u u
- 线性函数: f ( u ) = k u + c f(u)=ku+c f(u)=ku+c
- 非线性斜面函数
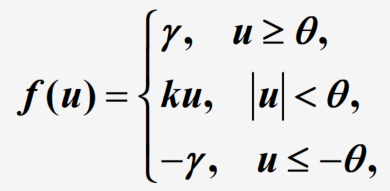
说明: θ , γ \theta,\gamma θ,γ>0为常数, γ \gamma γ称为饱和值为神经元的最大输出 - 阶跃函数
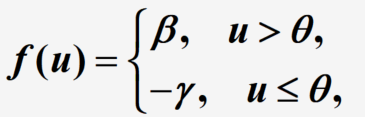
说明: θ , γ , β \theta, \gamma, \beta θ,γ,β均为非负常数, θ \theta θ为阈值
阶跃函数的特殊形式
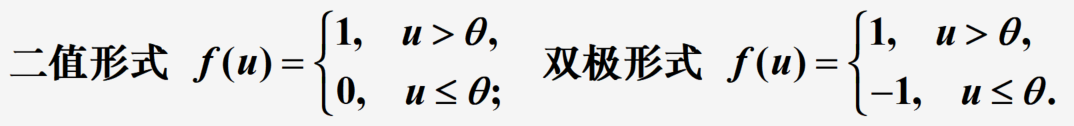
- S形函数
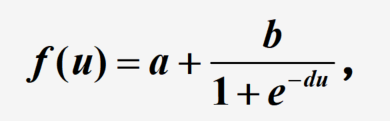
a , b , d a,b,d a,b,d为常数, f ( u ) f(u) f(u)的饱和值为 a a a和 a + b a+b a+b
基本模型
感知器
单层感知器是一个具有一层神经元、采用阈值激活函数的前向网络
通过对网络权值的训练,可以使感知器对一组输入矢量的响应达到0或1的目标输出,从而实现对输入矢量的分类
说明:有监督的权值训练,使用梯度下降法进行训练
示例说明

问题解析:记输入矢量的两个指标变量为
x
1
x_1
x1?和
x
2
x_2
x2?
代码
from sklearn.linear_model import Perceptron
import numpy as np
x0=np.array([[-0.5,-0.5,0.3,0.0],[-0.5,0.5,-0.5,1.0]]).T
y0=np.array([1,1,0,0])
md = Perceptron(tol=1e-3) #构造模型
md.fit(x0, y0) #拟合模型
print(md.coef_,md.intercept_) #输出系数和常数项
print(md.score(x0,y0)) #模型检验
print("预测值为:",md.predict(np.array([[-0.5,0.2]])))
BP神经网络
一种神经网络学习算法,由输入层、中间层和输出层组成,中间层可扩展为多层。相邻层之间各神经元进行全连接,而每层各神经元之间无连接,网络按有监督方式进行学习,权重更新使用梯度下降法和反向传播法实现
图示:
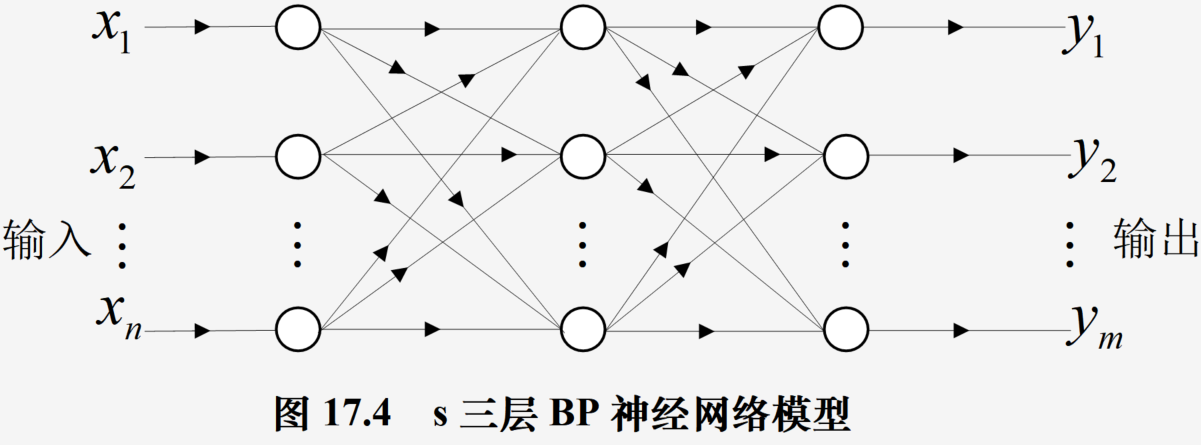
主要应用场景:
函数逼近:用输入向量和相应的输出向量训练一个网络以逼近某个函数
模式识别
预测
数据压缩:减少输出向量维数以便传输或存储
优化计算:解决非线性优化问题
理论上,对于一个三层或三层以上的BP网络,只要隐层神经元数目足够多,该网络就能以任意精度逼近一个非线性函数
RBF神经网络
由一个输入层、一个隐层和一个输出层组成
网络结构:
把网络看成对未知函数的逼近,任何函数都可以表示成一组基函数的加权和,这里的基函数即是隐藏层的传输函数。
设输入层的输入为
X
=
[
x
1
,
x
2
,
.
.
.
,
x
n
]
X=[x_1,x_2,...,x_n]
X=[x1?,x2?,...,xn?],实际输出为
Y
=
[
y
1
,
y
2
,
.
.
.
,
y
p
]
Y=[y_1,y_2,..., y_p]
Y=[y1?,y2?,...,yp?]

X
X
X为
n
n
n维输入向量,
C
i
C_i
Ci?为第
i
i
i个基函数中心,
C
i
C_i
Ci?与
X
X
X具有相同维数,
σ
i
\sigma_i
σi?为第
i
i
i个基函数的宽度,
m
m
m为感知单元的个数,
∣
∣
X
?
C
i
∣
∣
||X-C_i||
∣∣X?Ci?∣∣为向量
X
?
C
i
X-C_i
X?Ci?的范数,表示
X
X
X与
C
i
C_i
Ci?之间的距离,
R
i
(
X
)
R_i(X)
Ri?(X)在
C
i
C_i
Ci?处有一个唯一的最大值,随着
∣
∣
X
?
C
i
∣
∣
||X-C_i||
∣∣X?Ci?∣∣的增大,
R
i
(
X
)
R_i(X)
Ri?(X)迅速衰减到0
因而,当确定了RBF网络的聚类中心
C
i
C_i
Ci?、权值
w
i
k
w_{ik}
wik?及
σ
i
\sigma_i
σi?之后,就可求出给定某一输入,网络对应的输出值
RBF学习算法:
- 确定基函数的中心 C i C_i Ci?,利用一组输入计算 m m m个 C i C_i Ci?,并使 C i C_i Ci?尽可能均匀地对数据进行抽样,一般使用 k ? m e a n s k-means k?means聚类
- 确定基函数的宽度 σ i \sigma_i σi?,表示与每个中心相联系的子样本集种样本散布的一个测度。比如令 σ i \sigma_i σi?为 C i C_i Ci?与子样本集种样本点之间的平均距离
- 确定连接权值 w i k w_{ik} wik?
应用
数据预处理
归一化处理,将数据映射到
[
0
,
1
]
[0,1]
[0,1]或
[
?
1
,
1
]
[-1,1]
[?1,1]区间
第一种归一化处理方法,适用于激活函数为S形函数的情况
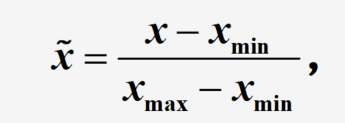
第二种归一化处理方法,适用于激活函数为双极S形函数的情况
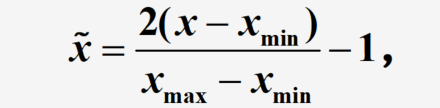
应用示例1

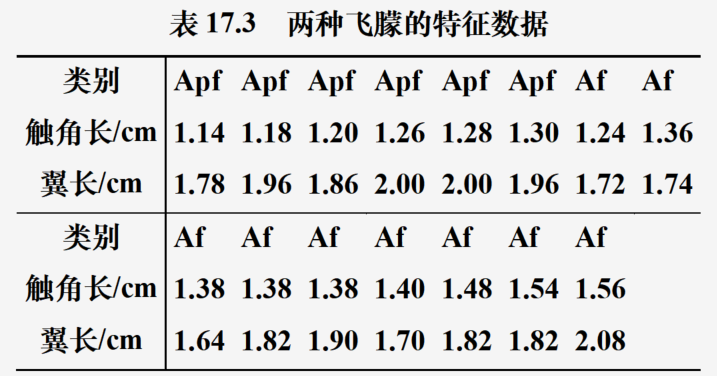
问题分析:根据飞朦的数据将其进行分类处理
代码:
from sklearn.neural_network import MLPClassifier
from numpy import array, r_, ones,zeros
x0=array([[1.14,1.18,1.20,1.26,1.28,1.30,1.24,1.36,1.38,1.38,1.38,1.40,1.48,1.54,1.56],
[1.78,1.96,1.86,2.00,2.00,1.96,1.72,1.74,1.64,1.82,1.90,1.70,1.82,1.82,2.08]]).T
y0=r_[ones(6),zeros(9)]
md = MLPClassifier(solver='lbfgs', alpha=1e-5,
hidden_layer_sizes=15)
md.fit(x0, y0); x=array([[1.24, 1.80], [1.28, 1.84], [1.40, 2.04]])
pred=md.predict(x); print(md.score(x0,y0)); print(md.coefs_)
print("属于各类的概率为:",md.predict_proba(x))
print("三个待判样本点的类别为:",pred);
应用示例2

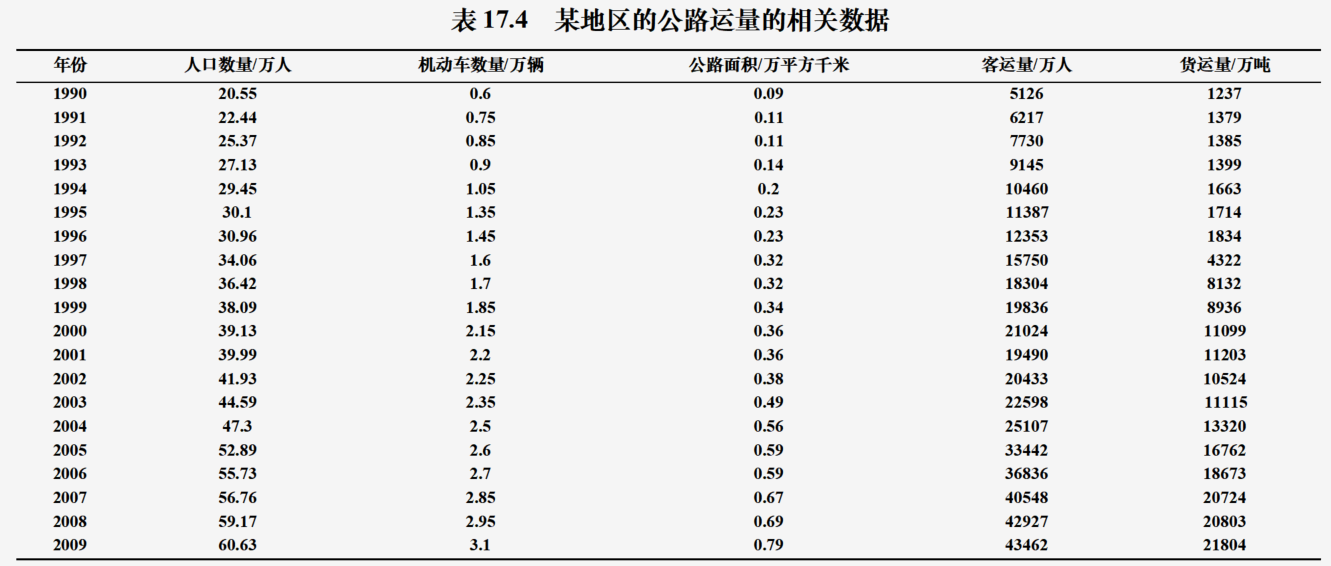
代码
from sklearn.neural_network import MLPRegressor
from numpy import array, loadtxt
from pylab import subplot, plot, show, xticks,rc,legend
rc('font',size=15); rc('font',family='SimHei')
a=loadtxt("Pdata17_5.txt"); x0=a[:,:3]; y1=a[:,3]; y2=a[:,4];
md1=MLPRegressor(solver='lbfgs', alpha=1e-5, hidden_layer_sizes=10)
md1.fit(x0, y1); x=array([[73.39,3.9635,0.988],[75.55,4.0975,1.0268]])
pred1=md1.predict(x); print(md1.score(x0,y1));
print("客运量的预测值为:",pred1,'\n----------------');
md2=MLPRegressor(solver='lbfgs', alpha=1e-5, hidden_layer_sizes=10)
md2.fit(x0, y2); pred2=md2.predict(x); print(md2.score(x0,y2));
print("货运量的预测值为:",pred2); yr=range(1990,2010)
subplot(121); plot(yr,y1,'o'); plot(yr,md1.predict(x0),'-*')
xticks(yr,rotation=55); legend(("原始数据","网络输出客运量"))
subplot(122); plot(yr,y2,'o'); plot(yr,md2.predict(x0),'-*')
xticks(yr,rotation=55)
legend(("原始数据","网络输出货运量"),loc='upper left'); show()
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!