2024华数杯国际赛AB题五小问完整思路+数据+四小问代码+后续高质量成品论文+运行结果高清图+参考文献

问题A：日本放射性废水 （AB题的完整资料放在文末了）

对于这次的华数杯A题，在我五月份完成的数维杯A题目中：

就已经完成过地下水污染物的公式推导：

因此，展示部分示例代码吧，我会在修改后，实际应用于我们这次的华数杯国际赛A题：

import numpy as np
import matplotlib.pyplot as plt

# 参数设定
L = 100.0  # 空间长度
T = 10.0   # 总模拟时间
Nx = 100   # 空间步数
Nt = 200   # 时间步数
D = 2.0    # 扩散系数
u = 1.0    # 对流速度

dx = L / Nx  # 空间步长
dt = T / Nt  # 时间步长

# 稳定性条件 (Courant-Friedrichs-Lewy 条件)
if u * dt / dx > 1:
    raise ValueError("稳定性条件未满足，请调整步长")

# 初始条件（在中心放置污染源）
C = np.zeros(Nx)
C[int(Nx / 2)] = 1.0

# 对流-扩散方程的数值解
for n in range(1, Nt):
    C[1:-1] = C[1:-1] - u * dt / (2 * dx) * (C[2:] - C[:-2]) + D * dt / dx**2 * (C[2:] - 2 * C[1:-1] + C[:-2])

# 绘制结果
plt.plot(np.linspace(0, L, Nx), C, label=f"t = {T}")
plt.title("对流-扩散方程的数值解")
plt.xlabel("位置")
plt.ylabel("浓度")
plt.legend()
plt.show()

#### 3.3 模拟调查结果：

#### 3.3.1 调查数据处理：

- 利用调查数据（Table 1）中的信息，结合 Tritium 传递模型，计算不同 Tritium 浓度下的鱼类 Tritium 浓度。

#### 3.3.2 渔业经济影响分析：

- 结合 Tritium 浓度和渔业经济模型，分析 Tritium 对渔业经济的长期影响。可以考虑使用微分方程或数值方法来模拟长期动态过程。

#### 3.4 结论与建议：

#### 3.4.1 判定所有海域是否会被污染：

- 利用 Tritium 传递模型，预测废水排放后的 Tritium 浓度动态，判断是否会对全球海域产生长期污染影响。

#### 3.4.2 污染最严重的地区：

- 根据模型模拟结果，判断哪些地区受到 Tritium 污染最严重，可能**需要分析 Tritium 浓度的时空分布**。

#### 3.4.3 向联合国环境计划提出建议：

- 基于模拟结果，提出建议，可能包括改善废水处理方法、加强监测体系、制定相关政策等。

其中，涉及到的分析?Tritium 浓度的时空分布过程，涉及到放射性物质在海水中的传播、吸收和释放等多个因素。以下是一个基本的时空分布分析的框架：

问题B：光伏发电

注意：【1】收集数据需要在论文中说明，并在参考文献中标注；

【2】代码中不要出现中文，注释写为中文是方便理解，提交的时候删除或翻译为英文。

问题一：中国的电力供应和许多因素相互作用。请研究它们之间的关系，并预测2024-2060年中国电力供应的发展趋势。

• 根据背景，电能产业与经济状况、居民消费水平、城镇化率、市场化等因素密切相关。由于数据中包含的因素较多，可以考虑寻找相关数据进行分析，利用Pearson（数据服从正态分布）或Spearman相关系数分析因素之间的关系。

采用电力消费量代表电能产业发展情况，地区生产总值代表各省经济状况，居民消费水平，城镇化率，发电量代表电能产业市场化

（国家统计局https://data.stats.gov.cn/easyquery.htm?cn=E0103）

Spearman具体算法和评价依据如下：

?????????????????（1）

其中，

表示相关系数，

分别表示两个变量第

个值，

分别表示两个变量的平均值。

相关系数的取值范围为

，存在以下关系：

对于这道题目而言，思路我也已经在上一个文章中讲解，所以我先分享一下数据吧：

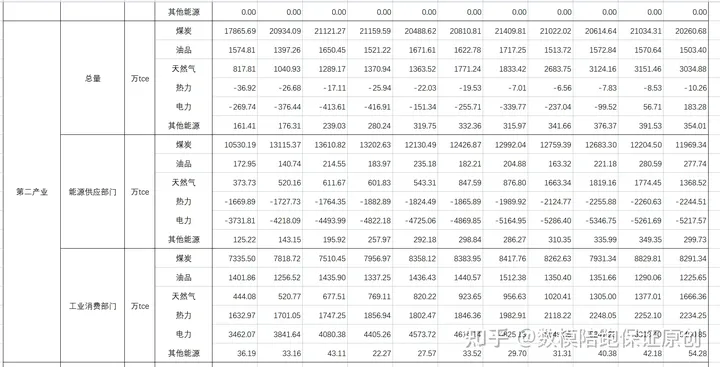
示例代码：
点击链接加入群聊【2024华数杯数学建模资料总群】：

import pandas as pd
from statsmodels.tsa.arima.model import ARIMA
import matplotlib.pyplot as plt

# 示例数据加载（您需要替换为实际的电力供应数据）
# 假设数据格式为两列：'Date' 和 'Electricity_Supply'
data = pd.read_csv('your_data.csv')
data['Date'] = pd.to_datetime(data['Date'])
data.set_index('Date', inplace=True)

# 数据可视化（初步了解数据走势）
data.plot()

# ARIMA模型建立
# 参数(p,d,q)需要根据您的数据调整
model = ARIMA(data, order=(5,1,0))
model_fit = model.fit()

# 预测
# 这里预测从2024年到2060年的数据
forecast = model_fit.forecast(steps=36)
forecast.plot()

# 显示图表
plt.show()