20240109-补 二叉树被感染的时间

题目要求

给你一棵具有唯一值的二叉树的根节点和一个整数起点。第 0 分钟时，感染从值为 start 的节点开始。

在下列情况下，每分钟都会感染一个节点：

• 节点当前未感染。
• 节点与已感染节点相邻。

返回整棵树被感染所需的分钟数。

Example 1:

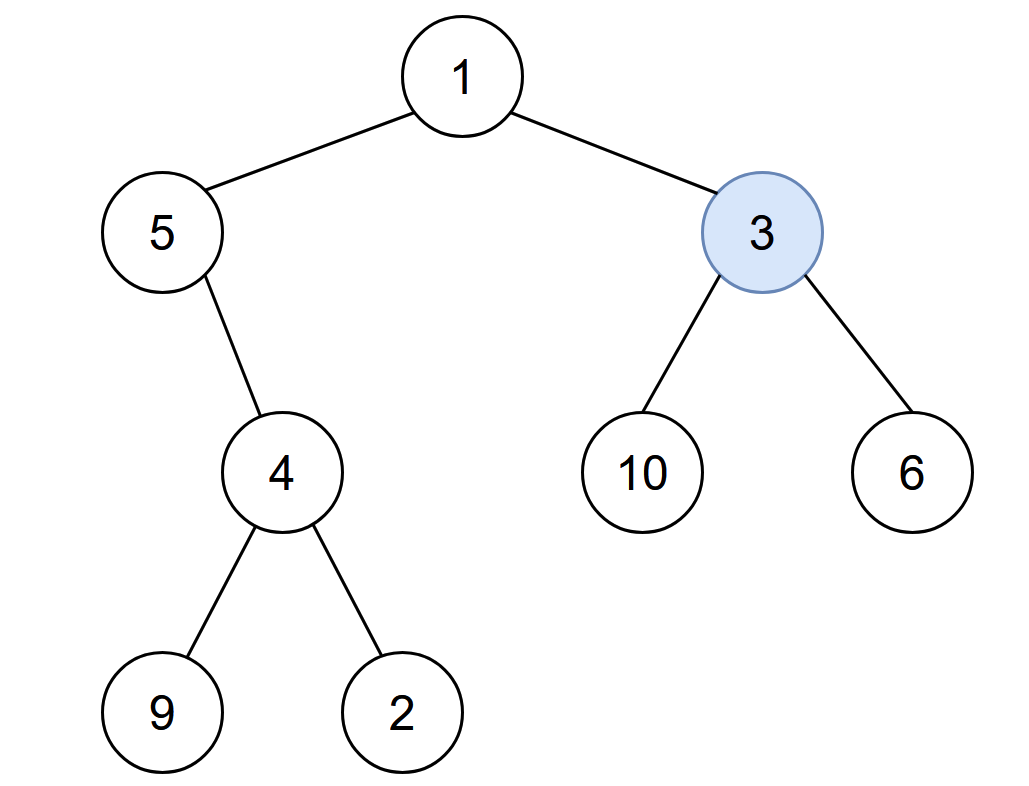
Input: root = [1,5,3,null,4,10,6,9,2], start = 3
Output: 4
Explanation: The following nodes are infected during:
- Minute 0: Node 3
- Minute 1: Nodes 1, 10 and 6
- Minute 2: Node 5
- Minute 3: Node 4
- Minute 4: Nodes 9 and 2
It takes 4 minutes for the whole tree to be infected so we return 4.

Example 2:

Input: root = [1], start = 1
Output: 0
Explanation: At minute 0, the only node in the tree is infected so we return 0.

思路?

树内的节点都是不重复的。因此我们只需要找到起始节点到根节点的最远距离就是结果。两条提示：

• 将树转换为无向图以使其更易于处理。
• 从起始节点开始使用BFS，求每个节点到起始节点的距离。答案是最大距离。

BFS简单，问题是如何从起始节点开始？如果具有初始值的节点刚好是根节点，那么题目就变成了与根节点的最大距离，也就是树的最大深度。

那么问题就转变成了，能否有一种方法，即使起始节点不是根节点，也能利用子树深度计算出起始节点的最大距离？

我们需要解决的第一个问题是：能否使用子树的深度来确定起始节点的最大距离？

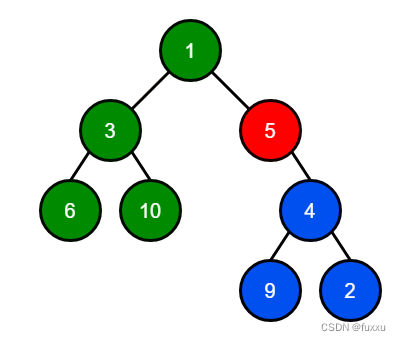
• 在上图中，起始节点是红色节点，即 5。
• subDepth = 2 // 红色子树的深度（起始节点下面的节点）
• depth = 1 // 红色节点的深度（起始节点）
• otherDepth = 2 // 绿色子树的深度（起始节点上方的节点）
• distance = depth + other_depth = 3 // 起始节点上方的任何节点到起始节点的距离
• maxDistance = max(distance, sub_depth) = 3

这项任务的一个难点是识别我们是否在遍历过程中遇到了起始节点。我们可以在遇到起始节点时返回负深度。这将标志着我们已经找到了起始节点，当我们遍历树时，只要遇到负深度，我们就知道子树包含起始节点。

此外，在遍历树的过程中，我们可能会在计算出树的每个部分的最大深度之前就找到起始节点。因此，我们需要保存最大距离，并在遍历树的其他部分时继续计算它。

核心思路

思路的核心在于如何处理起始节点。

1. 每次遍历节点时都新建一个深度depth，如果该节点是起始节点，则depth=-1，表示这是起始节点。
2. 如果是空节点则depth=0，返回。
3. 那么如果左右子树的depth都大于等于0，则表明起始节点不在左右子树中，那么这个结点的深度就可以写成depth=max(leftDepth, rightDepth) + 1;
4. 否则，如果左右子节点之一的深度返回-1，则表明当前节点下包含了起始节点：
   1. 此时开始处理起始节点，定义distance为abs(leftDepth)+abs(rightDepth)，即另一子树上最远节点的距离。
   2. 设置maxDistance=max(maxDistance, distance)，在距离变大时更新最远距离。
   3. 设置?depth = min(leftDepth, rightDepth) - 1来计算一个负数，表示子树包含起始节点，并代表起始节点与根节点的距离。最后一种情况是根节点不是起始节点，但其子树包含起始节点。在这种情况下，我们将设置 depth = min(leftDepth, rightDepth) - 1，这会得到一个负数，其绝对值代表起始节点到根节点的距离。为了计算起始节点到另一个子树中最远节点的距离，我们将把包含起始节点的子树的负深度绝对值和另一个子树的正深度绝对值相加，为了方便起见，我们可以直接取两个值的绝对值。然后，如果距离大于 maxDistance，我们就用距离更新 maxDistance。（这里的depth解决了上图中1->5结点的距离计算问题）

代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int maxDistance = 0;
    
    int traversal(TreeNode* root, int start) {
        int depth = 0;
        if (root == nullptr) {
            return depth;
        }

        int leftDepth = traversal(root->left, start);
        int rightDepth = traversal(root->right, start);

        if (root->val == start) {
            maxDistance = max(leftDepth, rightDepth);
            depth = -1;
        } else if (leftDepth >= 0 && rightDepth >= 0) {
            depth = max(leftDepth, rightDepth) + 1;
        } else {
            int distance = abs(leftDepth) + abs(rightDepth);
            maxDistance = max(maxDistance, distance);
            depth = min(leftDepth, rightDepth) - 1;
        }
        return depth;
    }
    int amountOfTime(TreeNode* root, int start) {
        traversal(root, start);
        return maxDistance;
    }
};

• Time complexity:?O(n)

  Traversing the tree with a DFS costs?O(n)O(n)O(n)?as we visit each node exactly once.

• Space complexity:?O(n)

lc的题解，我也没太理解，再想想。