大数据安全 | 期末复习（上）| 补档

📚概述??

🐇大数据的定义、来源、特点

1. 定义：无法在一定时间范围内用常规软件工具进行捕捉、管理和处理的数据集合，是需要新处理模式才能具有更强的决策力、洞察发现力和流程优化能力的海量、高增长率和多样化的信息资产。
2. 来源：从对象分为人、机、物等几大类，从领域分为互联网、物联网、生物医学。
3. 特点：规模大、变化快、种类多、价值密度低。

🐇大数据安全的含义

1. 保障大数据安全，是指保障大数据采集过程、计算过程、数据形态、应用价值的处理技术
2. 大数据用于安全，利用大数据技术提升信息系统安全效能和能力的方法，设计如何解决信息系统安全问题。

🐇大数据安全威胁

1. 大数据基础设施具有虚拟化和分布式特点，容易受到非授权访问、信息泄露或丢失、破坏数据完整性、拒绝服务攻击、网络病毒传播；
2. 大数据应用的生命周期中，数据存储是一个关键环节，尤其是非关系数据库带来如下安全挑战：模式成熟度不够、系统成熟度不够、服务器软件没有内置的足够的安全机制、数据冗余和分散性问题。
3. 网络安全是大数据安全防护的重要内容，安全问题随着网络节点数量的增加呈指数级上升；安全数据规模巨大，安全事件难以发现；安全的整体状况无法描述；安全态势难以感知等等。
4. 网络化社会使大数据易成为攻击目标：在网络化社会中，信息的价值要超过基础设施的价值；大数据蕴涵着人与人之间的关系和联系，使得黑客成功攻击一次就能获得更多数据。
5. 大数据滥用的风险：一方面，大数据本身的安全防护存在漏洞，安全控制力度不够。另一方面攻击者利用大数据技术进行攻击，最大限度地收集更多用户敏感信息。
6. 大数据误用风险：大数据的准确性和数据质量不高，对其进行分析和使用可能产生无效的结果，从而导致错误的决策。

🐇保障大数据安全

1. 围绕大数据全生命周期，即数据的产生、采集、传输、存储、处理、分析、发布、展示和应用、产生新数据等阶段进行安全防护。
2. 对大数据全生命周期阶段合并与精简，大数据应用过程可划分为4个环节：采集、存储、挖掘和发布。
3. 大数据保障技术可以从物理安全、系统安全、网络安全、存储安全、访问安全、审计安全、运营安全等角度进行考虑。
4. 保障大数据安全的目标：最大程度地保护具有流动性和开放性特征的大数据自身安全，防止数据泄露、越权访问、数据篡改、数据丢失、密钥泄露、侵犯用户隐私等问题的发生。

🐇采集、存储、挖掘环节的安全技术

1. 采集
   • 采集环节的安全威胁：数据损坏、丢失、泄露、窃取。
   • 采集环节的安全机制：身份认证、数据加密、完整性保护、抗重放攻击、端到端的数据安全传输（采用SSL VPN（安全套接层，虚拟专用网），有Web浏览器模式、客户端模式、Lan到Lan模式）。
2. 存储
   • 存储环节的安全威胁：数据被窃取、丢失、破坏、隐私或机密数据的泄露。
   • 存储环节的安全机制：隐私保护（数据脱敏、变换、匿名化），数据加密（静态数据是指不需要参与计算的数据，要先加密再存储；动态数据是指需要检索或参与计算的数据，要动态加密），备份与恢复（异地备份、RAID、数据镜像）
3. 挖掘
   • 挖掘环节的安全威胁：第三方在数据挖掘的过程中植入恶意程序、窃取系统数据。
   • 挖掘环节的安全机制：身份认证（基于秘密信息 / 信物 / 生物特征）、访问控制（自主访问控制DAC、强制访问控制MAC、基于角色的访问控制RBAC）。
4. 发布
   • 发布环节的安全威胁：泄密、泄露隐私、不合规范。
   • 发布环节的安全机制：安全审计（基于日志/网络监听/网关/代理的）、数据溯源（对应用周期的各个环节的操作进行标记和定位，溯源方法：标注法、反向查询法、数字水印）。

🐇大数据用于安全

1. 安全监测与大数据的融合技术，利用大数据技术实时监控海量、多样、快速和复杂的数据，有效提高安全监测的效果和能力。
2. 大数据技术将极大扩展安全分析的深度和广度，把传统的数据安全分析的被动的事后分析变成主动地事前防御，能够更好地感知网络安全态势。

🐇隐私的定义、属性、分类、保护、面临威胁

1. 定义：隐私是与个人相关的、具有不被他人搜集、保留和处分的权利的信息资料集合，并且它能够按照所有者的意愿在特定时间、以特定方式、在特定程度上被公开。
2. 基本属性：保密性、个人相关、能够被所有者处分
3. 分类：个人隐私（任何可以确定特定个人或与可确定的个人相关，但个人不愿意暴露的信息，譬如：就诊记录）、共同隐私（不仅包含个人隐私，还包含所有个人共同表现出但不愿意被暴露的信息，譬如：平均薪资）
4. 保护
   • 个人属性的隐私权：譬如姓名、身份、肖像、声音等，直接涉及个人领域的第一层次，是保护的首要对象。
   • 个人资料的隐私权：譬如消费习惯、病历、犯罪前科等记录，若其涉及的客体为一个人，则这种资料含有高度的个人特性而常能辨识该个人的本体，即“间接”的个人属性，也应以隐私权加以保护。
   • 通信内容的隐私权：通信内容包含个人的思想与情感，原本存于内心，别人不可能知道，因而应以隐私权保护，以保护个人人格的完整发展。
   • 匿名的隐私权：匿名权利的适度许可，可以鼓励个人的参与感，并保护其自由创造力空间，真知直谏推动社会的整体进步。
5. 面临大数据的威胁
   • 大数据时代带来信息存储和管理的集中化，一切皆可量化。
   • 大数据通常包含了大量的用户身份信息、属性信息、行为信息，极易造成用户隐私泄露。
   • 大数据的多源性使得来自各个渠道的数据可以用来进行交叉检验，导致隐私泄露。
   • 数据存储过程：大数据环境下，用户无法知道数据确切的存放位置，用户对其个人数据的采集、存储、使用、分享无法有效控制。
   • 数据传输过程：大数据环境下，数据传输将更为开放和多元化，传统物理区域隔离的方法无法有效保证远距离传输的安全性，电磁泄漏和窃听将成为更加突出的安全威胁。
   • 数据处理过程：大数据环境下，部署大量的虚拟技术，资源动态共享增加了访问控制和身份认证的管理难度，基础设施的脆弱性和加密措施的失效可能产生新的安全风险。

🐇安全基本概念

1. 脆弱性：系统在设计、实现、操作或管理中的缺陷或弱点，可被攻击者利用以至于给系统造成损失或危害。比如软硬件漏洞，访问权限设置缺陷等。
2. 威胁：存在于环境、能力、行动或事件中可能会破坏安全并造成伤害的安全隐患，也就是说，威胁可能利用脆弱性并造成损失。比如勒索软件、蠕虫等恶意程序为有意威胁，地震、洪涝灾害为自然威胁，误操作为无意威胁等。
3. 攻击：蓄意试图规避目标系统的安全服务并违反其安全策略的智能行为。以震网病毒事件为例，通过震网病毒利用PLC脆弱性的行为就是攻击。
4. 风险：一种损失预期，表示为某一特定威胁利用某一特定脆弱性产生特定有害结果的可能。以震网病毒事件为例，其中震网病毒为威胁，可编程控制单元（PLC）中的代码存在被篡改的脆弱性，此系统的风险是当震网病毒作用于PLC之后造成铀浓缩离心机受损的可能。

🐇安全需求及对应的安全事件

• 保密性
  • 保证信息 / 数据不会被泄露给未经授权的个体；
  • 防御方法：加密解密算法；
  • 例子（要知道安全事件对应的安全需求）：
    • 智能家居中，若智能电表的用电数据没有良好加密，则不法分子可利用这些用电数据推断用户的习惯，从而猜测用户当前是否在家。
    • 弱口令攻击。
• 完整性
  • 保证信息 / 数据不会被未经授权的个体修改；
  • 防御方法：Hash 函数，纠错码，消息认证码；
  • 例子：
    • 智能安防系统的系统完整性是指它能在发生非法入侵等情况时及时报警，这是它的预期功能。 若安防系统功能出现问题，其后果可能是金钱损失，甚至威胁用户人身安全。
    • 2016年5月7日，一辆启用半自动驾驶（Autopilot）功能的特斯拉电动汽车与一辆大型卡车相撞，司机在事故中丧生。这是与自动驾驶相关并造成人员伤亡的第一起交通事故。这次事件的原因是Autopilot没有检测到卡车的白色侧面。
    • 2019年，Carnegie Mellon University的研究人员通过在摄像机镜头上放置贴纸，使得分类器误分类，例如STOP标志识别成成限速标志。
• 可用性
  • 保证信息 / 数据能够被已授权的个体访问；
  • 破坏可用性的攻击：Denial of Service (Dos), Distributed Dos (DDoS)。
  • 例子：
    • 在智能家居的业务中，首要的是整个智能家居系统是可用的。若照明、安防、多媒体等系统不能工作，将给用户带来极大的困扰。
    • 2017年5月， WannaCry勒索病毒感染了西班牙电信等公司，其利用 “永恒之蓝”（EternalBlue）漏洞加密系统数据，从而勒索用户。该事件是典型的传统互联网数据可用性被破坏的例子。在该事件中，用户计算机的所有数据都被加密，无法获取。
    • 2016年10月，大半个美国遭遇了集体“断网” ，各大网站无法访问，包括Twitter、Spotify、Netflix、Github、Airbnb等。原因是美国最主要的DNS服务商Dyn遭遇了大规模DDoS攻击。DDoS攻击是通过大量的垃圾请求阻塞服务器，使正常用户的请求得不到响应。最终破坏互联网业务可用性。
    • Stuxnet蠕虫是第一个被发现专门用于定向攻击基础（能源）设施的蠕虫病毒，国家电网、核电站、水坝水利设施等都是该病毒的攻击目标。目前全球已有约4.5万个网络被感染，其中60%主机位于伊朗境内 。伊朗政府已经确认核电站遭到攻击，导致铀浓缩离心机受损。
    • 2015年12月23日，乌克兰电力部门遭受到恶意代码攻击，导致了八万用户数小时的停电事故。
• 真实性
  • 保证信息 / 数据确实来自其所生成的消息源，即可确定数据来源；
  • 防御工具：密码方案，数字签名，Hash函数，消息认证码，质询-响应协议。
• 不可抵赖性
  • 保证信息 / 数据交互的所有参与者均不能否认曾经发送过的消息和数据；
  • 防御方法：数字签名。

📚古典密码学

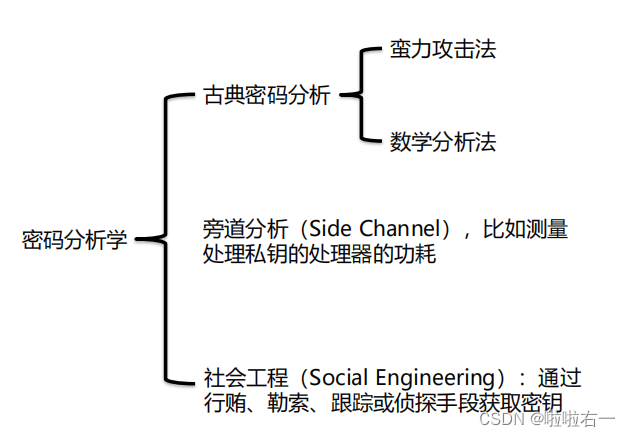
🐇里程碑事件

1. 1883年科克霍夫第一次提出密码编码原则。科克霍夫假设：密码分析者知道双方使用的密码系统，包括明文的统计特性、加密解密体质等，唯一不知道的是密钥。
   

2. 1949年香农发表The communication theory of serect systems

3. 1971-1973年，IBM Waston实验室的Horst Feistel等人发表了几篇对称加密的技术报告

4. 1974年，IBM提交了LUCIFER，后来成为DES

5. 1976年diffie和hellman的文章new directions in cryptography提出了公钥密码的概念

6. 1977年Rivest，Shmir&Adleman提出了RSA公钥算法

🐇扩散和混淆的概念

• 香农的贡献：定义了理论安全性，提出扩散和混淆原则，奠定了密码学的理论基础。
• 扩散：将每一位明文尽可能地散布到多个输出密文中去，以更隐蔽明文数字的统计特性。
• 混淆：使密文的统计特性与明文密钥之间的关系尽量复杂化，使攻击者无法获得密钥。

🐇攻击的分类

1. 唯密文攻击（Cipher-only attack）: 攻击者有一个或多个密文，攻击需要统计分析；
2. 已知明文攻击（Known-plaintext attack）: 攻击者有一份密文和对应的明文，进行算法和密钥推导；
3. 选择明文攻击（Chosen-plaintext attack）: 攻击者有机会使用加密机，因此可以选择任何明文并产生对应的密文，攻击概率更大；
4. 选择密文攻击（Chosen-cipher attack）: 攻击者有机会使用解密机，因此可以选择一些密文并产生对应的明文。
5. 攻击难度由下到上逐渐增加。

🐇模运算🍎

• 同余：若 a mod n = b mod n ，则 a 和 b 是模 n 的同余，即 a ≡ b (mod n)
• 同余性质：若n整除（|）a-b，则 a ≡ b (mod n)
• 模算术运算的性质：
  • [(a mod n) + (b mod n)]mod n = (a + b)mod n
  • [(a mod n) – (b mod n)]mod n = (a - b)mod n
  • [(a mod n) x (b mod n)]mod n = (a x b)mod n
    
    （132，图里的123错了）

🐇移位加密

• 加密过程：y = x + k (mod 26)
• 解密过程：x = y - k (mod 26)
• 其中，k就是加密密钥。

🐇仿射加密

• 加密过程：给定密钥(α,β)，𝑦 = 𝛼𝑥 + 𝛽 (mod 26)
• 解密过程：x=1/α(y?β) (mod 26)
• 1/α不是α的倒数，而是乘法逆元。若 a * x ≡ 1 (mod) b, a, b 互质，则称 x 为 a (模b)的逆元。

  #令b=13
  alpha = [1, 3, 5, 7, 9, 11, 15, 17, 19, 21, 23, 25]
  alpha_inverse = [1, 9, 21, 15, 3, 19, 7, 23, 11, 5, 17, 25]
  

  

🐇维吉尼亚密码

• 列出明文并按照密钥长度分组，用密钥对每个组内字母进行移位加密
  
  

📚DES

• 梳理流程，了解大体过程
• DES实验

🐇混淆与扩散

• 扩散：为了隐藏明文统计属性而将一个明文符号的影响扩散到多个密文符号的加密操作，直接影响是修改明文中的1位会导致平均一半的输出位发生变化，常用于DES，可通过位置换实现。
• 混淆：使密钥与密文之间的关系尽可能模糊的加密操作，在DES和AES中都有使用，可通过替换技术实现。

🐇Feistel加密

• 总共16轮，每轮做如下操作：
  
  
  
  
  

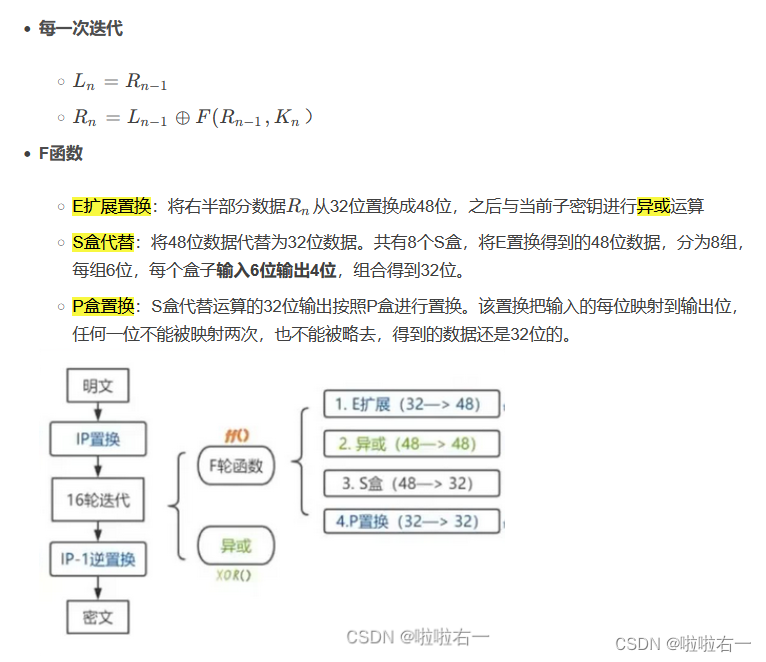
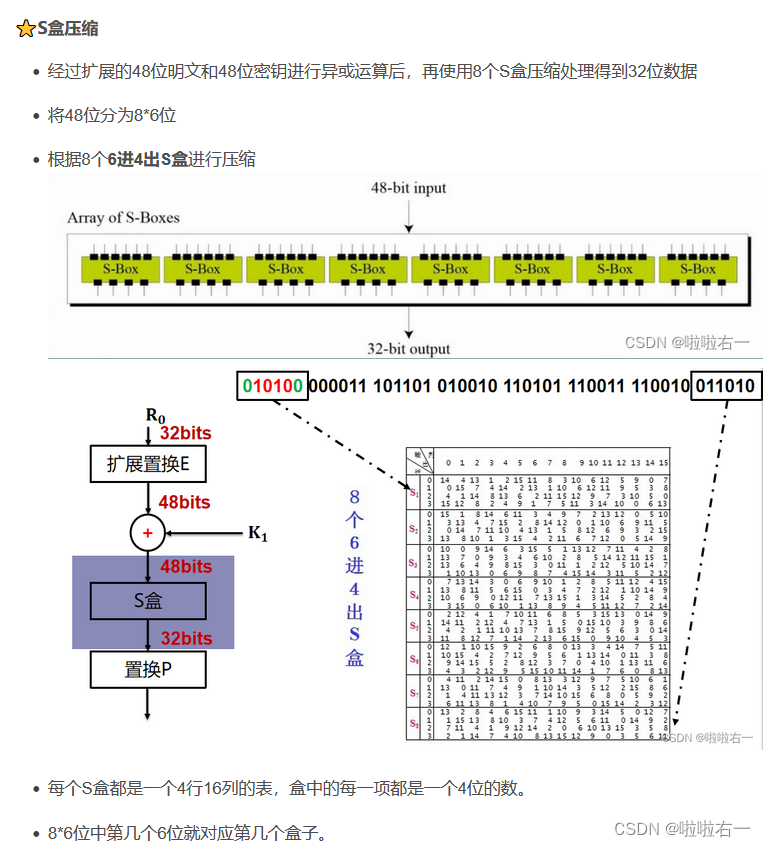
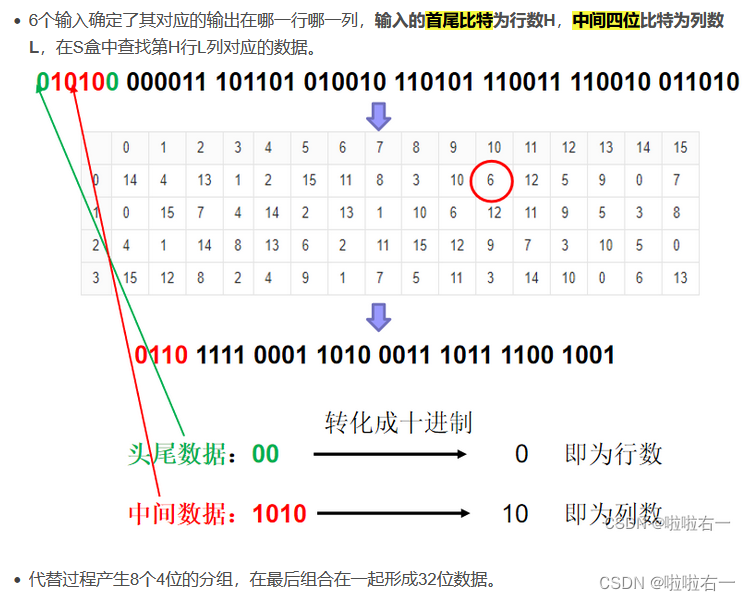
🐇DES密钥生成

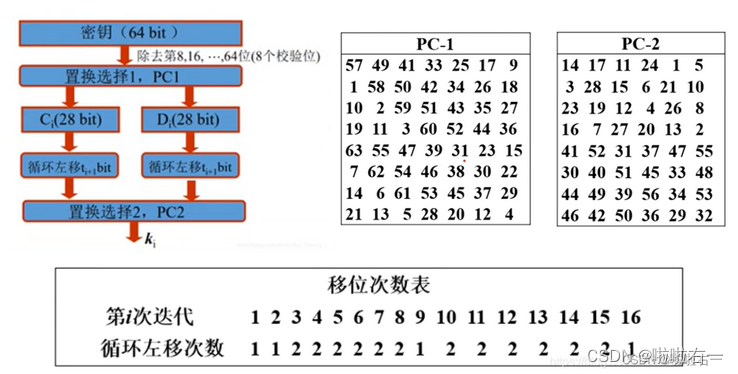
🐇DES流程

3DES：由三个连续的DES加密组成，也称之为三重DES。

📚数论🍎

🐇欧几里得算法

• 欧几里德算法又称辗转相除法：用于计算两个整数a，b的最大公约数。其计算原理依赖于下面的定理：gcd(a,b) = gcd(b,a mod b)
  
  

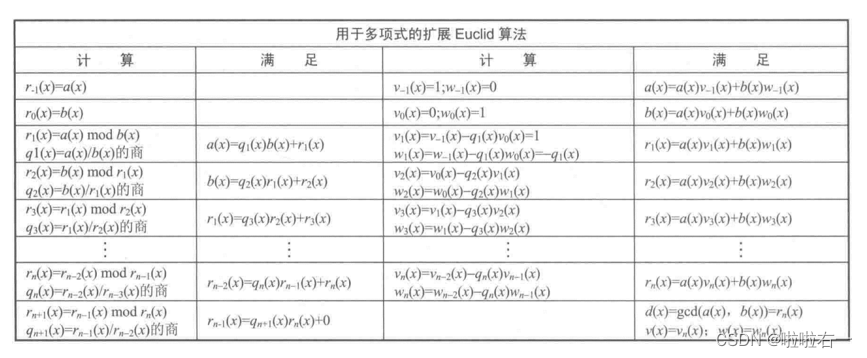
🐇拓展欧几里得算法

• 拓展欧几里得算法：对于给定整数a,b，拓展的欧几里得算法不仅可以计算出最大公因子d, 而且可以得到两个整数x,y，并满足：ax + by = d = gcd (a, b)。
• 如果a,b 互素，b 有模a的乘法逆元：1/b= y
  
  

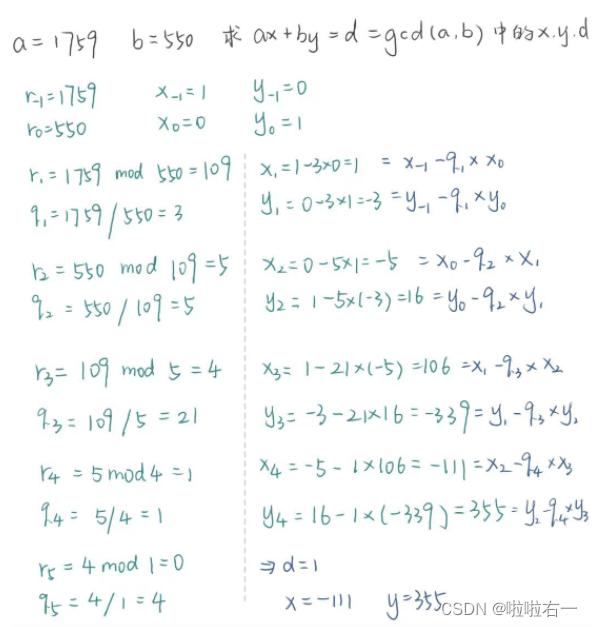
🐇欧拉函数

• 给定正整数m，所有整数按照模m是否同余分为两两不相干的集合，每一个集合称为模m的剩余类，在剩余类的所有整数中，通常用最小非负整数表示这个剩余类。
  
• 剩余类互素/互质定义：在模m的一个剩余类当中，如果有一个数与m互素，则该剩余类中所有的数均与m互素，这时称该剩余类与m互素。
• 欧拉函数定义：与m互素的剩余类的个数称为欧拉函数，记为φ(m)。𝜑(𝑚) 等于 Z_m当中与m互素 的数的个数。对于任意一个素数m，φ(m)=m-1。
  

---

🐇有限域运算

• 元素个数有限的域称为有限域，元素的个数是该有限域的阶。反之，称为无限域。
• 阶为$p^n$的有限域可记为GF($p^n$)；有p个元素的有限域记为GF§。
• 给定一个素数p，有限域GF§被定义为整数 {0, 1, …, p-1}的集合Z_p，其运算是模p的算术运算。
• 性质：GF§中任意元素w，存在其逆元$w^{?1}=z$，使得$w\times z\equiv 1modp$。

---

• 普通多项式运算
  

---

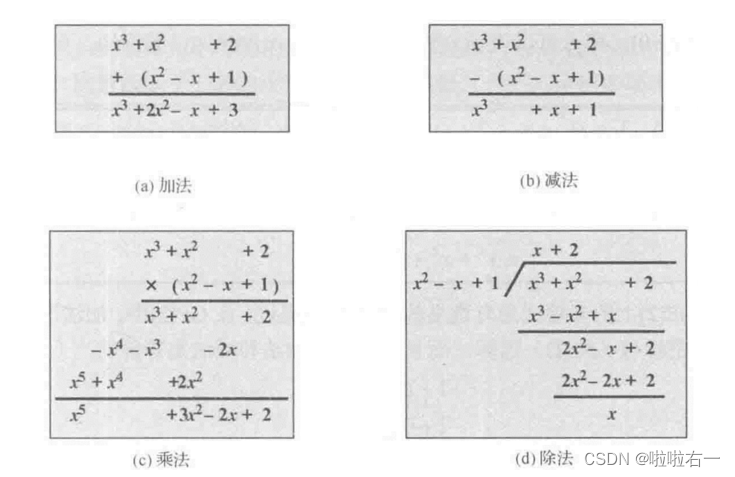
• 系数在$z_p$中的多项式运算：系数在$z_p$中的多项式运算要求在计算每个系数的值时需要做模计算。
  
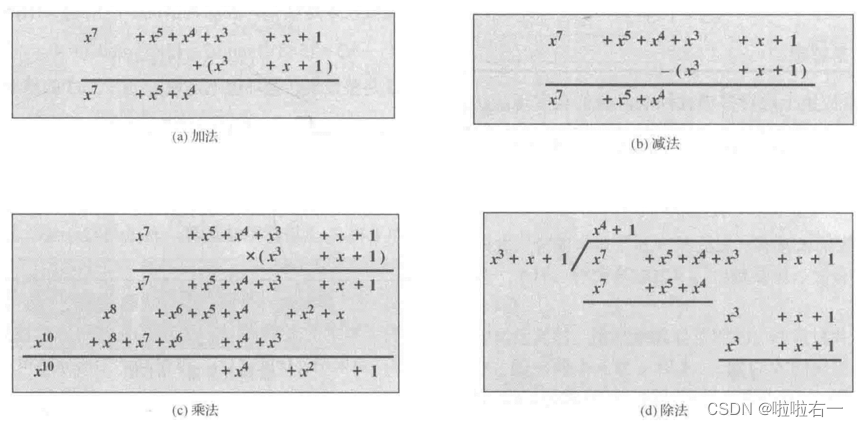
• 不可约多项式：在域F上，若一个多项式不能写成两个多项式的乘积，则被称为不可约多项式或素多项式。
• 最大公因式：
  • 最大公因式c(x)=gcd?(a(x), b(x))服从下列条件：多项式c(x)能同时整除a(x)和b(x)，a(x)和b(x)的任何公因式都是c(x)的因式。
  • 性质： gcd?(a(x), b(x))=gcd?(a(x) mod b(x), b(x))
    

---

• 在有限域GF($2^n$)上的多项式模运算：GF($p^n$) ：给定一个素数p，元素个数为$P^n$的有限域被定义为整数{0,1,…, $P^{n?1}$}的集合$Z_p$，即p是域，n是多项式的阶（最高n-1）
  
  

---

• 有限域GF($2^n$)中的逆元也使用扩展的欧几里得算法求得。
  
  
• 生成元
  

---

$GF(P)$	$GF(2^n)$
系数需要mod P	系数mod 2；指数上，如果乘法运算的结果是次数大于n?1的多项式，那么必须将其除以某个次数为n的既约多项式m(x)并取余

📚AES

• S-AES加密实验
• 2000年10月2日，NIST宣布Rijndael作为新的AES
  

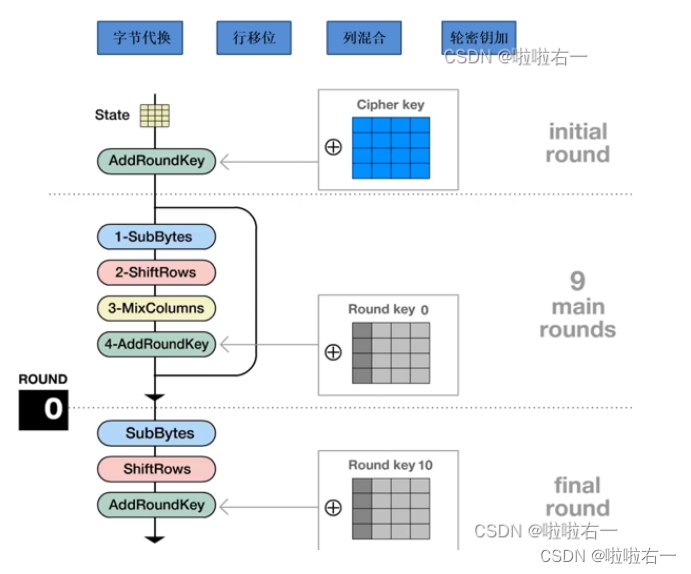
🐇密钥扩展算法

🐇字节替换

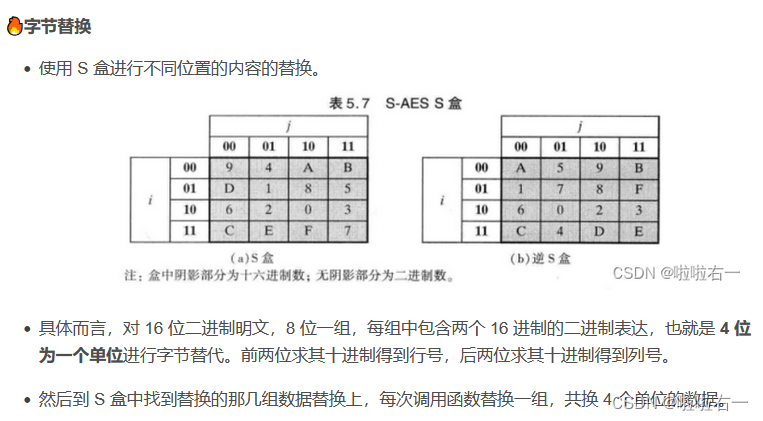
🐇轮密钥加

🐇行变换

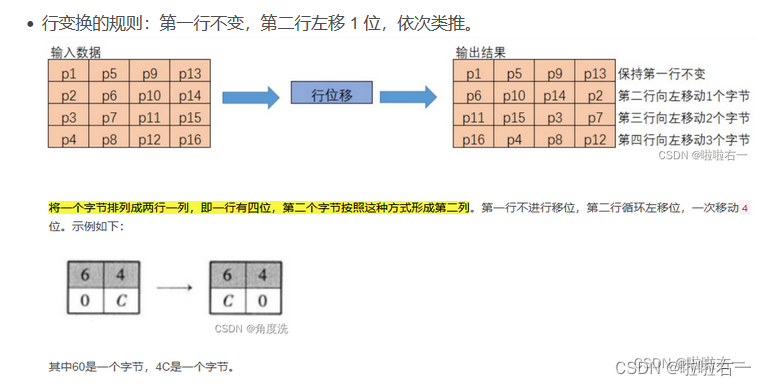
🐇列混淆

📚RSA

---

---

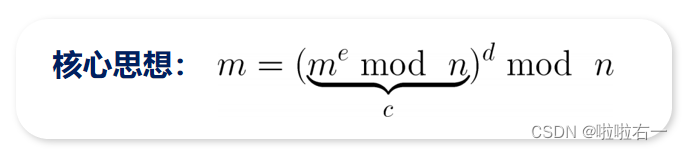
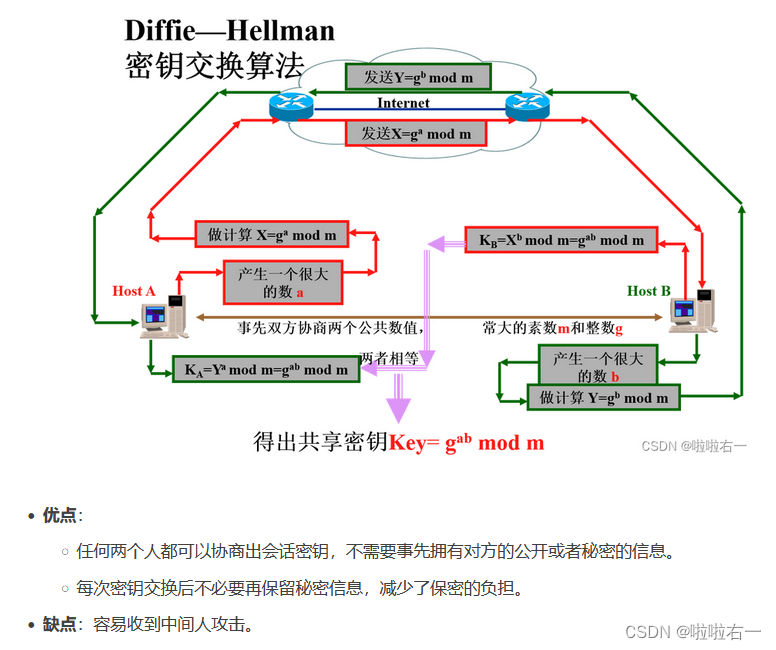
📚DH

• DH实验
• 安全性基于有限域上计算离散对数，只能用于两个用户之间交换密钥，不能进行加解密。
  

📚ElGamal公钥密码

• ElGamal公钥密码实验
• p的位数要在1024以上。
• 这是基于离散对数的数学困难问题。
  
  

---

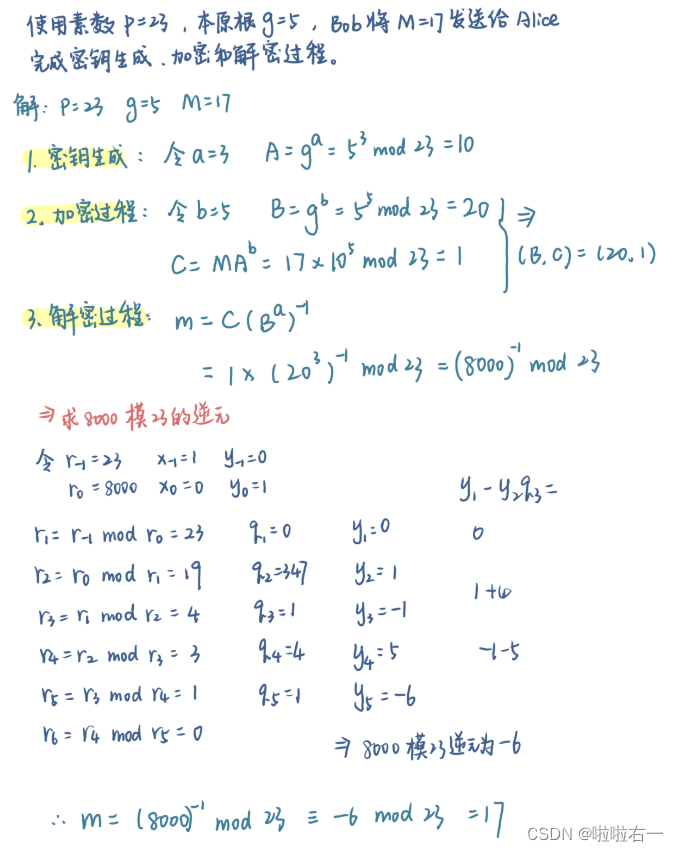
📚椭圆曲线公钥密码体制（ECC）

• 只关注有限域P阶（$2^n$先不管）
• 安全性基础：椭圆曲线群上的离散对数问题。目前，最好的解法仍然是指数时间。
• 在密码学中，可将椭圆曲线方程限制在如下形式：$y^2=x^3+ax+b,a,b\in F$

🐇Zp上的椭圆曲线🍎