opencv#28 图像卷积

图像卷积

图像卷积是图像处理中最为基础的操作之一，其常用在图像的边缘检测，图像的去噪声以及图像压缩等领域。

图像卷积主要步骤:

Step1:将卷积模板旋转180°。

Step2:卷积模板移动到对应位置。

Step3:模板内求和，保存求和结果。

Step4:滑动卷积模板，处理所有结果。

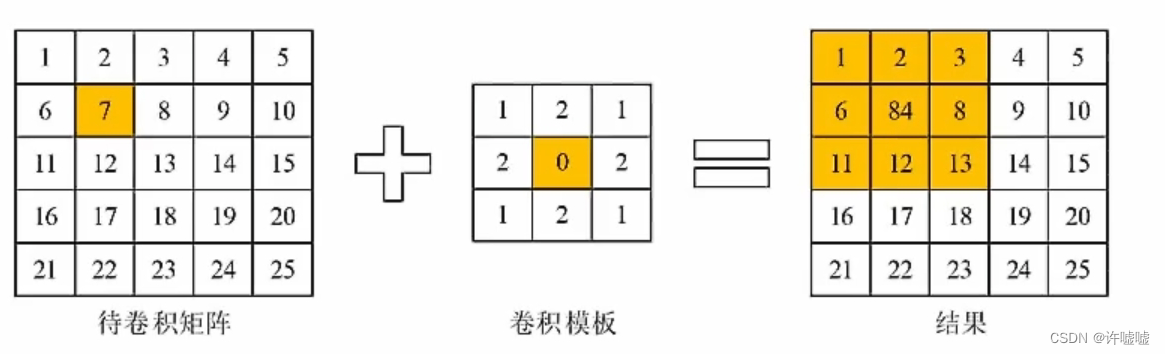
? 卷积函数在这里称卷积模板，卷积模板通常是一个方形的卷积，同时也是一个奇数的卷积，卷积模板通常使用的是一个中心对称的形式。

? 例如上图，在将模板旋转180°时，需要确定一个旋转中心，也就是我们卷积模板的中心，围绕这个中心旋转180°得到的结果便是我们需要进行卷积操作的结果。由于，我们常用的卷积模板是一个中心对称的模板，所以我们常看到在进行卷积时，无需进行180°的操作，?但是，我们要清楚，卷积首先重要的第一步是对模板进行旋转，否则，当我们使用非中心对称模板的时候，那么我们再对卷积模板进行旋转之后，得到的结果与原结果不一致，此时进行卷积旋转和不旋转的结果时不同的，之后将我们的模板移动到需要进行卷积图像或矩阵的对应位置，例如上图，我们将模板移动到像素值为7的中心区域上，我们将卷积模板完整覆盖在此区域上，第三步，将模板覆盖的区域与模板求和，首先是对应位置求乘积 ，也就是1*1+2*2+3*1....依次相乘再相加，得到的结果便是我们卷积之后的结果，将此结果替换掉原先待卷积矩阵中，这样得到的结果便是我们卷积之后的矩阵的结果。之后将卷积模板移动到下一位，也就是将中心位置覆盖在像素值为8的区域，继续对应位置相乘再相加得到的结果为96，这个96就替换掉原先图像中的8，依次运行下去，每一步都进行替换。? ?这里可以发现，在移动的时候，我们的中心像素只能覆盖我们原先像素的中心位置，其边缘位置是没有办法进行处理的，如上图，我们卷积后的结果只有中心3*3的像素进行了改变，而其他周围的像素是没有进行改变的，我们知道，对于图像来说，最边缘的一行和一列像素对图像整体的信息表达没有太多的作用，但是有的时候我们依然想得到一个边缘经过处理的结果，因此，我们将原图像边缘进行扩充一行一列像素，那么此时再进行卷积运算时，我们的卷积模板中心就可以覆盖在我们原图像中最边缘区域上，这样，我们可以在边缘上依次移动，得到结果，这里面对于边缘填充有很多种方法，例如，可以用全是0来填充，也可以复制最边缘的值进行填充。当我们的卷积模板为5*5的形式，那么我们对于边缘扩充就要两行两列，这样才能保证最边缘的图像能够被我的卷积模板中心所覆盖。

? 可以发现，进行卷积后，像素值变得很大，扩大了很多倍数，若像素值是0~255之间，当中心像素为25时，可能计算结果就会超过最大值，那么就会影响卷积结果，因此在卷积操作的时候，我们还需要进行归一化的操作，就是将卷积模板进行归一化，将模板中每一个数除以模板中所有系数之和得到归一化后的结果，这样得到的结果就可以保证不会经过卷积后数值不会越界。

图像卷积函数

filter2D()

void cv::filter2D(InputArray   src,
                  OutputArray  dst,
                  int          ddepth,
                  InputArray   kemel,
                  Point        anchor = Point(-1,-1),
                  double       deta = 0,
                  int          borderType = BORDER_DEFAULT
                 )

·src:输入图像。

·dst:输出图像，与输入图像具有相同的尺寸和通道数。（经过卷积后的图像，由于卷积运算可能会出现小数，因此输入和输出图像的数据类型可能会不同）

·ddepth:输出图像的数据类型(深度)，根据输入图像的数据类型不同拥有不同的取值范围。（例如输入图像是8U形式，那么输出图像就可包含8U，但是若输入的是一个32F的形式，那么输出图像中就不可能包含8U形式，因为经过处理后得到的结果精度一定比没有经过处理的精度高。）

·kernel:卷积核（卷积模板），CV_32FC1（浮点类型单通道矩阵）类型的矩阵（通常矩阵形式是一个奇数的正方形矩阵）。

·anchor:内核的基准点(锚点)，默认值(-1,-1)代表内核基准点位于kernel的中心位置。

·delta:偏值，在计算结果中加上偏值（默认情况下此值为0，也就是卷积后的结果是没有进行偏移的）。

·borderType:像素外推法选择标志（也就是对图像进行外围扩充的形式）。

在了解上函数后，发现并没有进行卷积模板的旋转，因此我们需要人在进行卷积函数时，人为旋转180°。

示例

#include <opencv2/opencv.hpp>
#include <iostream>

using namespace cv; //opencv的命名空间
using namespace std;

//主函数
int main()
{
	//待卷积矩阵
	uchar points[25] = { 1,2,3,4,5,
	6,7,8,9,10,
	11,12,13,14,15,
	16,17,18,19,20,
	21,22,23,24,25 };
	Mat img(5, 5, CV_8UC1, points);
	//卷积模板(需要32FC1形式，所以要设置为float)
	Mat kernel = (Mat_<float>(3, 3) << 1, 2, 1,
		2, 0, 2,
		1, 2, 1);
	Mat kernel_norm = kernel / 12;//卷积模板归一化
	Mat result, result_norm; //未归一化的卷积结果和归一化的卷积结果
	filter2D(img, result, CV_32F, kernel, Point(-1, -1), 2, BORDER_CONSTANT);
	filter2D(img, result_norm, CV_32F, kernel_norm, Point(-1, -1), 2, BORDER_CONSTANT);
	cout << "result" << endl << result << endl;

	//图像卷积
	Mat lena = imread("E:/opencv/opencv-4.6.0-vc14_vc15/opencv/lenac.png");
	if (lena.empty())
	{
		cout << "请确认图像文件名称是否正确" << endl;
		return -1;
	}
	Mat lena_filter;
	filter2D(lena, lena_filter, -1, kernel_norm, Point(-1, -1), 2, BORDER_CONSTANT);
	imshow("lena_filter", lena_filter);

	waitKey(0);//等待函数用于显示图像
	return 0;

}

运行程序后，发现图像卷积最大的作用是可以对图像进行模糊，模糊的作用可以减小噪声，同时也可以增加后续处理的精度，这里面虽然进行了边缘扩充，但是对于整个图像来说并没有影响我们观看图像所能获得的信息。