FPGA 查找表的用途和内部功能

翻译自

本文介绍了构成现场可编程门阵列 (FPGA) 的查找表 (LUT)。

FPGA 及其内部架构

现场可编程门阵列 (FPGA) 提供了可重新配置的设计平台，这使得它们在数字设计人员中很受欢迎。 FPGA 的典型内部结构（图 1）由三个主要元素组成：

• 可配置逻辑块 (CLB)（如图 1 中的蓝色框所示）是 FPGA 用来实现逻辑功能的资源。每个 CLB 由一组片组成，这些片可进一步分解为一定数量的查找表 (LUT)、触发器 (FF) 和多路复用器 (Mux)。
• FPGA 外围可用的输入/输出块 (IOB) 有助于外部连接。这些可编程模块将信号“传送至”FPGA 芯片或“传送自”FPGA 芯片。图 1 将 IOB 显示为封闭在 FPGA 边界内的一组矩形框（紫色外框）。
• 开关矩阵（如图 1 中的红色线所示）是 FPGA 内的互连线状布置。这些为 CLB 提供连接或提供专用的低阻抗、最小延迟路径（例如全局时钟线）。
  
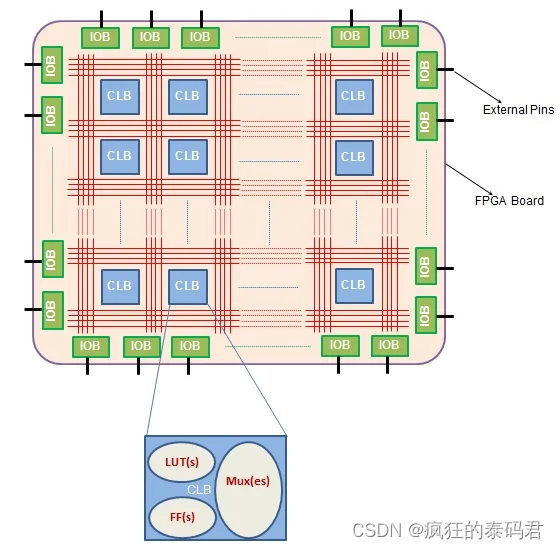
  图 1：典型 FPGA 的内部架构。

查找表 (LUT) 概述

FPGA 系列彼此不同的特征之一是它们的逻辑资源。例如，Spartan-II FPGA (PDF) 的每个 CLB 由两个片组成，每个片有两个 LUT。 Spartan 6 (PDF) 有两个切片（slices），每个切片有四个 LUT。在内部，LUT 由 1 位存储单元（可编程以保存“0”或“1”）和一组多路复用器组成。这些 SRAM 位中的一个值将在 LUT 的输出处可用，具体取决于馈送到多路复用器的控制线的值。

LUT 可用的输入数量决定了其大小。一般来说，具有 n 个输入的 LUT 由 $2^n$ 个单位存储单元组成，后跟一个 $2^n$:1 多路复用器或其等效设备（例如，两个 $2^n$-1:1 多路复用器后跟一个 2:1 多路复用器）。

由 4 个 SRAM 位和 4:1 多路复用器组成的 2 输入 LUT 的具体示例如图 2a 所示。接下来，图 2b 显示了其等效架构，但将 4:1 多路复用器表示为 2:1 多路复用器树。

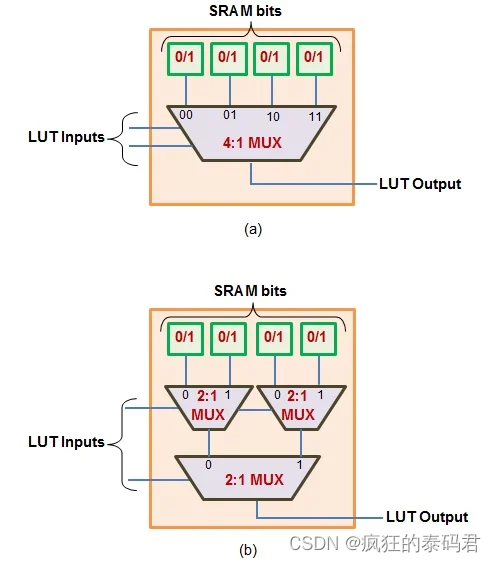图2(a)和2(b)：4位LUT的内部结构

使用LUT实现逻辑函数

FPGA 利用其 LUT 作为实现任何逻辑功能的初步资源。这实际上是一个两阶段的过程。
首先，构成布尔函数的输入变量的每个组合的输出值存储在LUT的SRAM单元中。此后，根据用户提供的输入变量的组合，适当的存储器位将出现在 LUT 的输出引脚上。这是因为用户提供的输入位充当 LUT 内部多路复用器的选择线。

情况 1：输入变量的数量等于 LUT 输入的数量

假设我们要使用 4 输入 LUT 实现四个输入变量 A、B、C 和 D 的布尔函数。这里，仅当两个输入变量中的任何一个为 1 时，让输出变高。与之对应的真值表如下所示。

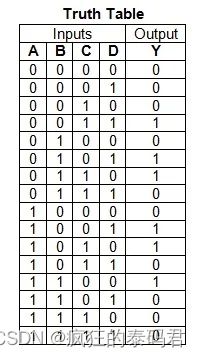
使用 FPGA 实现此功能时，A、B、C 和 D 将作为 LUT 的输入。接下来，每个组合的输出变量值（在真值表的最后一列中提供）将存储在 SRAM 单元中，如图 3 所示。
现在，如果 ABCD = 0101，则当第六个存储单元的内容到达输出引脚时，LUT 的输出 Y 将采用值 1（如图 3 中的红色不连续线所示）。

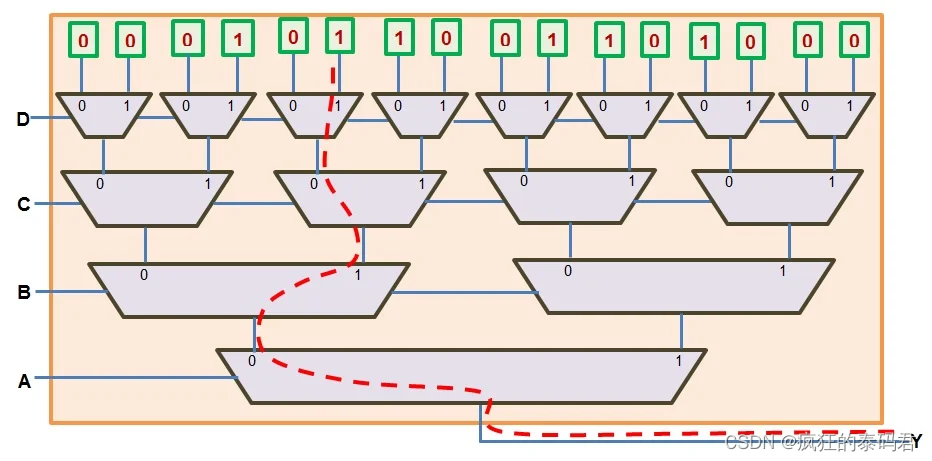
图 3：使用 4 输入 LUT 实现 4 输入布尔函数

情况 2：输入变量的数量大于 LUT 输入的数量

当我们的FPGA没有4输入LUT而只有3输入LUT时我们该怎么办？我们可以在里面实现我们的功能吗？我们可以。
图4展示了这种实现模式。此处，两个 3 输入 LUT 共享同一组三个较低有效输入（B、C 和 D）。这些 LUT 中任何一个的输出都使用 2:1 多路复用器路由到 Y 输出位（由红色不连续线显示），其选择线将是我们的第四个变量 A (MSB)。
在此图中，最后一个 2:1 多路复用器被认为是构成 CLB 的切片内存在的多路复用器。

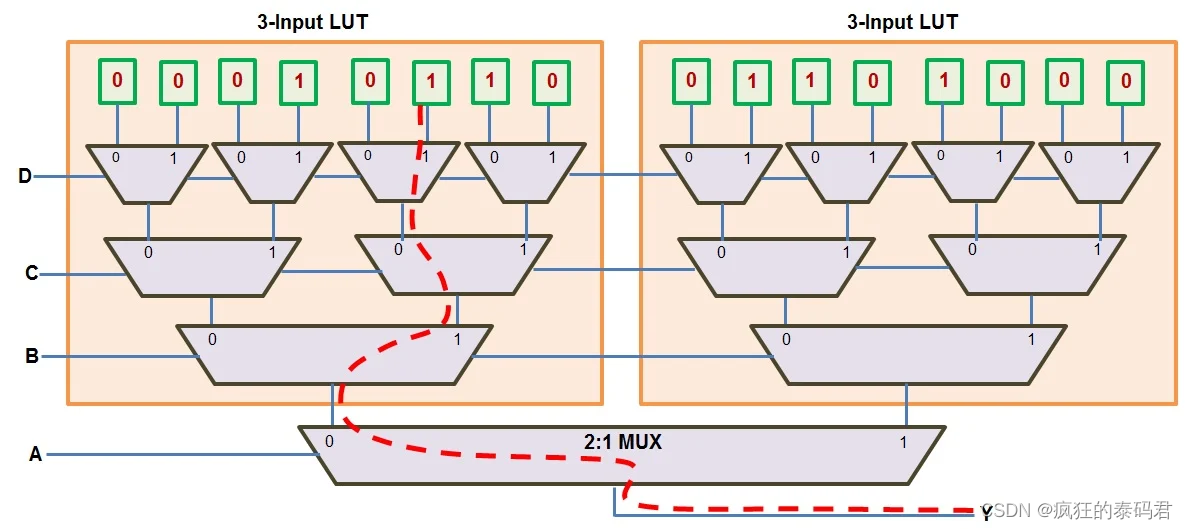
图 4：使用 3 输入 LUT 和 Mux 的组合实现 4 输入布尔函数

情况 3：输入变量的数量小于 LUT 输入的数量

现在，假设我们有一个由 4 输入 LUT 组成的 FPGA，我们需要在其中实现 3 输入逻辑功能。
在这种情况下，构成布尔表达式的三个输入变量驱动 LUT 的三个 (LSB) 输入，而其第四个输入 (MSB) 将被拉低。然后，8 个 SRAM 单元被配置为保存函数的输出值，而其他 8 个单元被设置为零。

例如，图 5 显示了使用 4 输入 LUT 实现全加器求和输出的可能方法。这里，所经过的路径（红色不连续线）显示了 ABC = 011 的情况，此时输出 Y 变为 0。
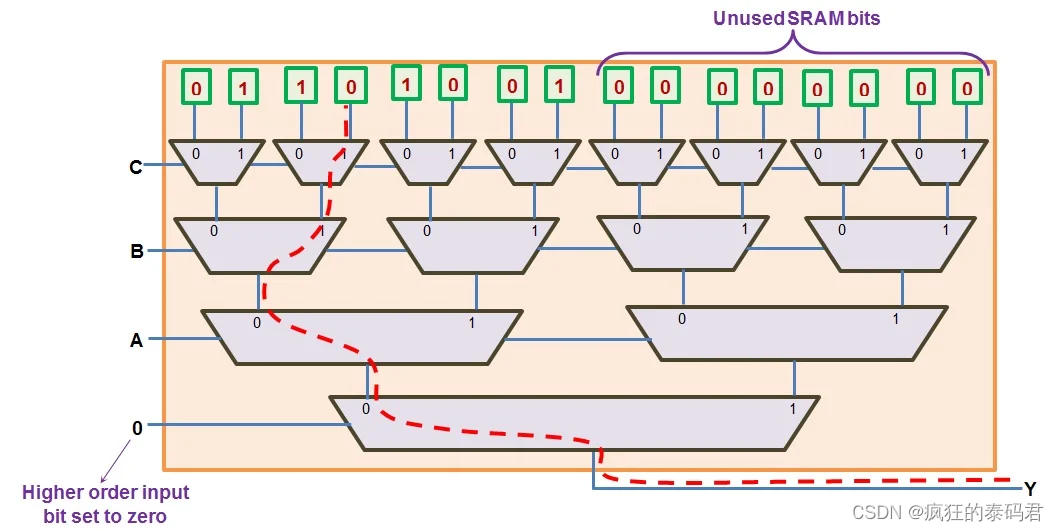图 5：使用 4 输入 LUT 实现 3 输入逻辑功能

对所提供案例的分析使我们得出这样的结论：只要需要，FPGA 就可以使用 FPGA 的 LUT 以及多路复用器等附加组件来有效地实现任何组合设计。
另一方面，如果我们需要实现时序电路，那么除了多路复用器之外，甚至切片中存在的触发器也需要考虑。事实上，这就是 FPGA 实现几乎所有布尔表达式的方式，无论其复杂程度如何。

LUT 的重要性

假设我们必须计算跨越一定范围的离散输入变量的三角函数，例如计算余弦。直接完成时，必须计算每个输入的余弦。这个过程的计算成本很高，因此效率低下，特别是在范围很大的情况下。

相反，我们可以预先计算范围内所有可能输入的余弦并??将它们存储在 LUT 中。此后，计算任何输入值的余弦将涉及从查找表中获取（而不是计算）相应值的操作。这将大大减少运行时间，从而提高效率。

此外，请注意，LUT 的 SRAM 单元是影响 FPGA 重新配置能力的重要因素之一。这是因为每次器件加电时，构成它们的配置位都可以更改，从而改变它们的功能。

例如，只需更改存储在其 SRAM 单元 (PDF) 中的值，即可使充当加法器的 LUT 充当减法器。然而，我们不应忘记，几乎所有基于 LUT 的操作都容易出现故障。