代码随想录算法训练营第三十天|332.重新安排行程、51. N皇后、37. 解数独

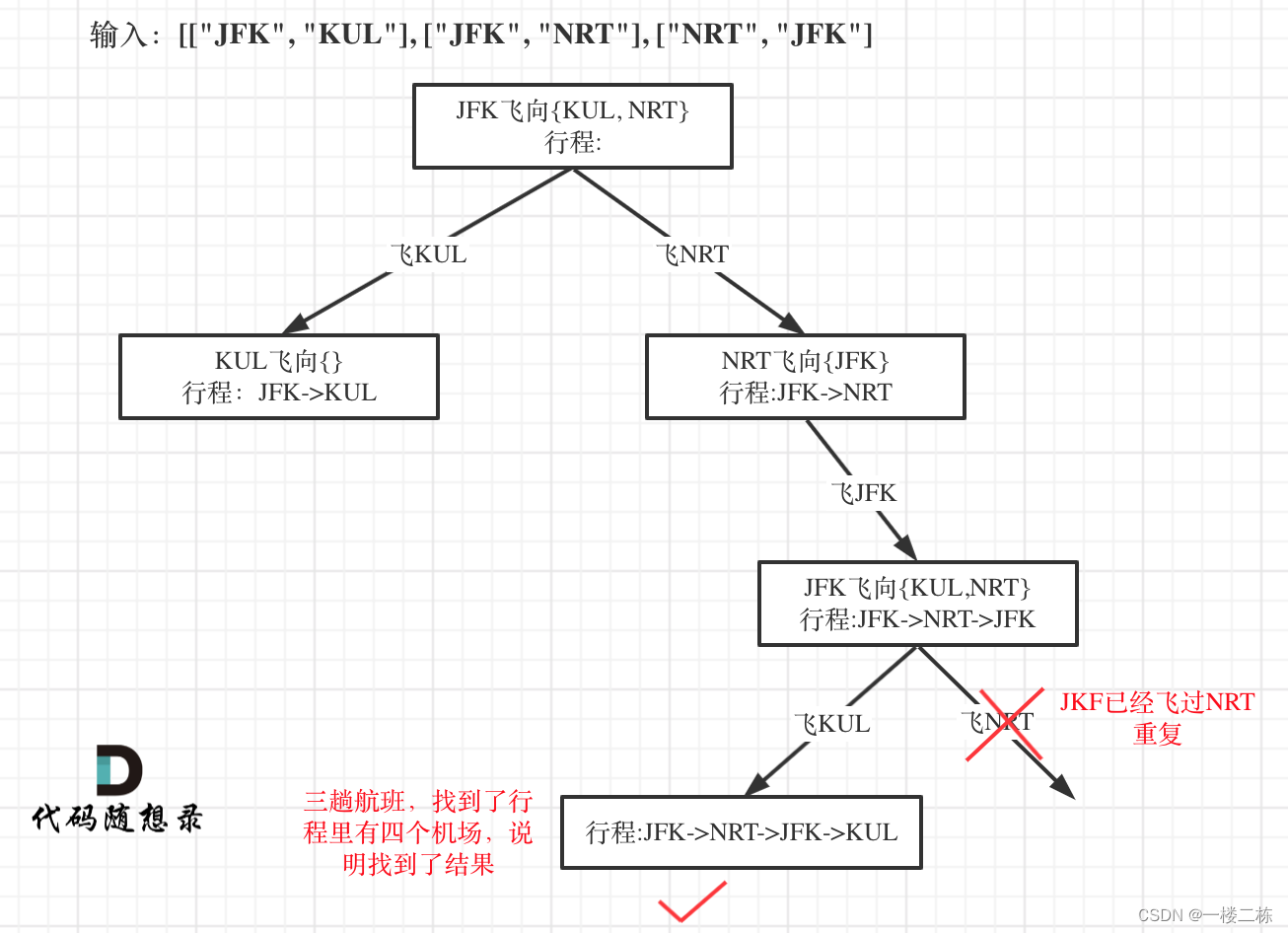
题目：332.重新安排行程

文章链接：代码随想录

题目链接：力扣题目链接

图释：

class Solution {
public:
    // unordered_map<出发机场, map<抵达机场, 航班次数>> targrts;
    unordered_map<string, map<string,int>> targrts;
 
    bool backtracking(int ticketNum, vector<string>& result){
        // 所有机票都要用一次 
        if(result.size() == ticketNum+1){ //航线次数+1
            return true;
        }
        // targrts[result[result.size()-1]] 从结果集里的最后一个目的地，作为出发地，找到以航班中的航线
        for(pair<const string, int>& targrt: targrts[result[result.size()-1]]){
            if(targrt.second > 0){ // 检测本航线是否飞过
               result.push_back(targrt.first);
               targrt.second--;
               if(backtracking(ticketNum, result)) return true; // 如果下层递归有返true则继续向上返回true
               // 没有返回找到航班则回溯
               result.pop_back();
               targrt.second++;
            }
        }
        // 遍历完，以该地点作为出发地的航线都不行，则返回
        return false; 
    }

    vector<string> findItinerary(vector<vector<string>>& tickets) {
        targrts.clear();
        vector<string> result;
        // vec = ["MUC","LHR"] 遍历赋值给vec
        for(const vector<string> vec : tickets){
            // <MUC <LHR, 1>>
            targrts[vec[0]][vec[1]]++;
        }
        result.push_back("JFK"); // 放入首发机场
        backtracking(tickets.size(), result); // 航线次数
        return result;
    }
};

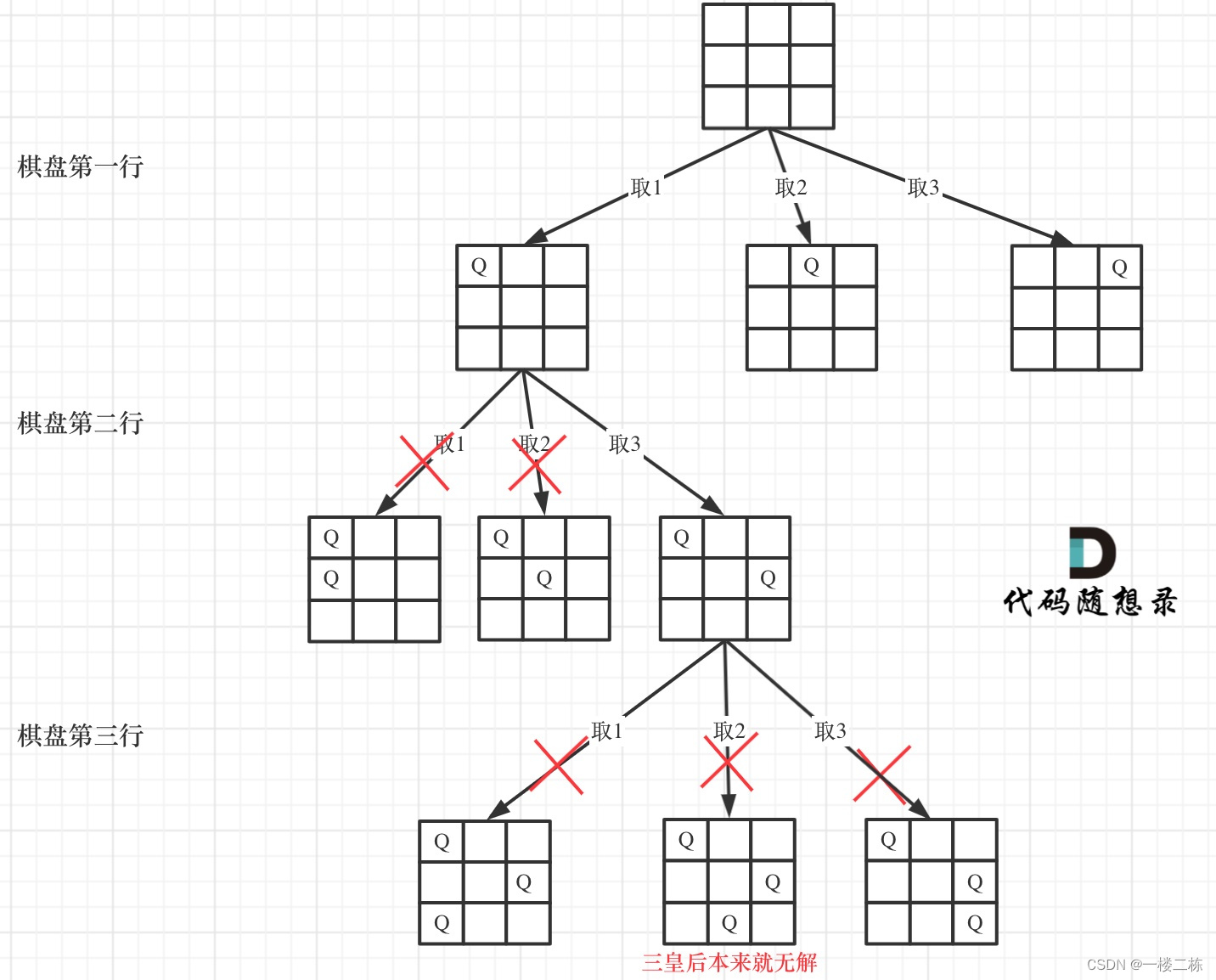
题目：51. N皇后

文章链接：代码随想录

视频链接：LeetCode:51.N皇后

题目链接：力扣题目链接

图释：

class Solution {
public:
    vector<vector<string>> result;
    bool isValid(int row, int col, vector<string> chessboard, int n){
       // 检测列
       for(int i=0; i<n; i++){
           if(chessboard[i][col] == 'Q') return false;
       }
       // 检测45度角(上一行的左上角) 因为还没遍历到下一行，所以不用判断
       for(int i=row-1, j=col-1; i>=0 && j>=0; i--,j--){
           // 当row==clo==0时，不会进入
           if(chessboard[i][j] == 'Q') return false; // 一直循环向↖找
       }
        for(int i=row-1, j=col+1; i>=0 && j<=n; i--,j++){
           if(chessboard[i][j] == 'Q') return false; // 一直循环向↗找
       }
       return true;
    }    
    // 传入棋盘
    void backtracking(vector<string> chessboard, int n, int row){
        if(row == n){
            // 在进入递归之前就判断该位置能否放入皇后了，所以当递归到最后一行，说明是合法的
            result.push_back(chessboard);
            return;
        }
        // 树层逻辑  遍历某行的每一列
        for(int col=0; col<n; col++){
            if(isValid(row, col, chessboard, n)){ // 判断该位置是否合法
               chessboard[row][col] = 'Q'; // 放置皇后
               backtracking(chessboard, n, row+1);
               chessboard[row][col] = '.'; // 回溯，撤销皇后
            }
        }
        // 可加可不加，不加的话就是当层遍历完，没有的话，自动退出
        return ;
    }
  
    vector<vector<string>> solveNQueens(int n) {
        result.clear();
        // 根据传入的n构建棋盘格
        std::vector<std::string> chessboard(n, std::string(n, '.'));
        backtracking(chessboard, n, 0);
        return result;
    }
};

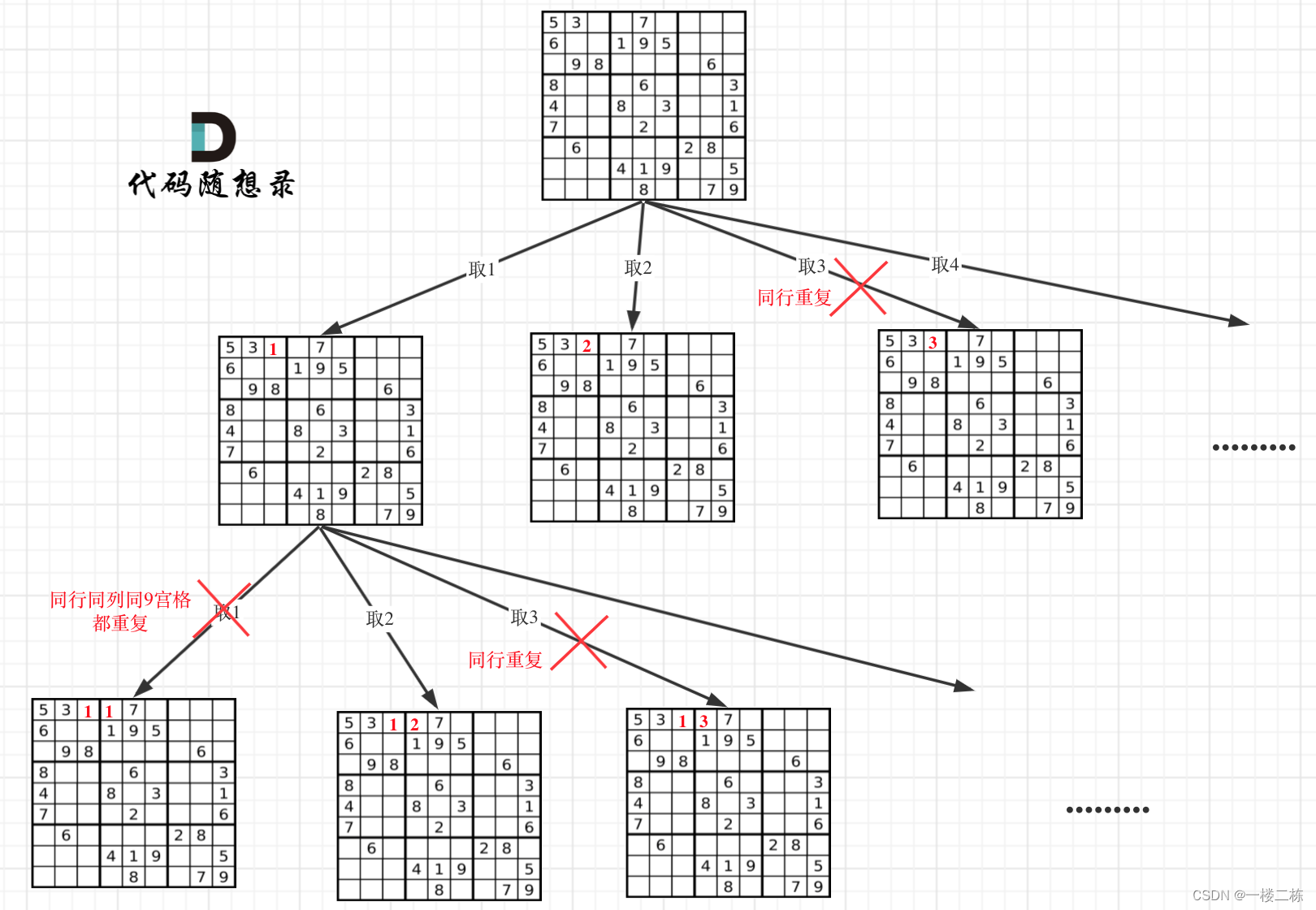
题目：37. 解数独

文章链接：代码随想录

视频链接：LeetCode:

题目链接：力扣题目链接

图释：

class Solution {
public:
    bool isValid(int row, int col, char k, vector<vector<char>>& board){
        for(int i=0; i<9; i++){// 判断行有无重复
           if(board[row][i]==k)return false;
        }
        for(int j=0; j<9; j++){// 判断列有无重复
           if(board[j][col]==k)return false;
        }
        // 判断格子中有无重复
        int startRow = (row/3)*3; 
        int startCol = (col/3)*3;
        for(int i=startRow; i<startRow+3; i++){ // 注意这里是小于，不用等号
            for(int j=startCol; j<startCol+3; j++){
                if(board[i][j]==k) return false;
            }
        }
        // 如果遍历完都没有不合法，则合法
        return true;
    }

    // 如果是需要遍历所有的路径，把结果放到result中就用void 不需要返回值，由终止条件终止
    // 如果只需要找到一条合法的路径，则用bool，当找到一条时，一层一层向上返回true，不需要再遍历
    bool backtracking(vector<vector<char>>& board){
        // 二维递归
        for(int i=0; i<board.size(); i++){  // 行
            for(int j=0; j<board[0].size(); j++){ // 列

                // 如果当前位置不为空，则向下继续
                if(board[i][j] !='.'){
                    continue;
                }
                // 循环放入1-9个数
                for(char k='1'; k<='9'; k++){

                    // 判断这个位置和否合法
                    if(isValid(i,j,k,board)){
                        board[i][j] = k; // k 是 char类型
                        if(backtracking(board)) {
                           return true; // 如果下层递归返回true,说明找到解法，继续向上进行返回
                        }
                        // 没有找到，则换另外一个数再进行尝试
                        board[i][j] = '.';
                    } 
                }
                // 如果9个数都尝试完了都不符合，则返回false
                return false;
                }
        }
        // 如果遍历完网格中所有的格子都没有false的话，则说明找到解法了
        return true;
    }

    void solveSudoku(vector<vector<char>>& board) {
        backtracking(board);
    }
};