DP专题9 理解01背包问题

本题链接：晴问算法

题目：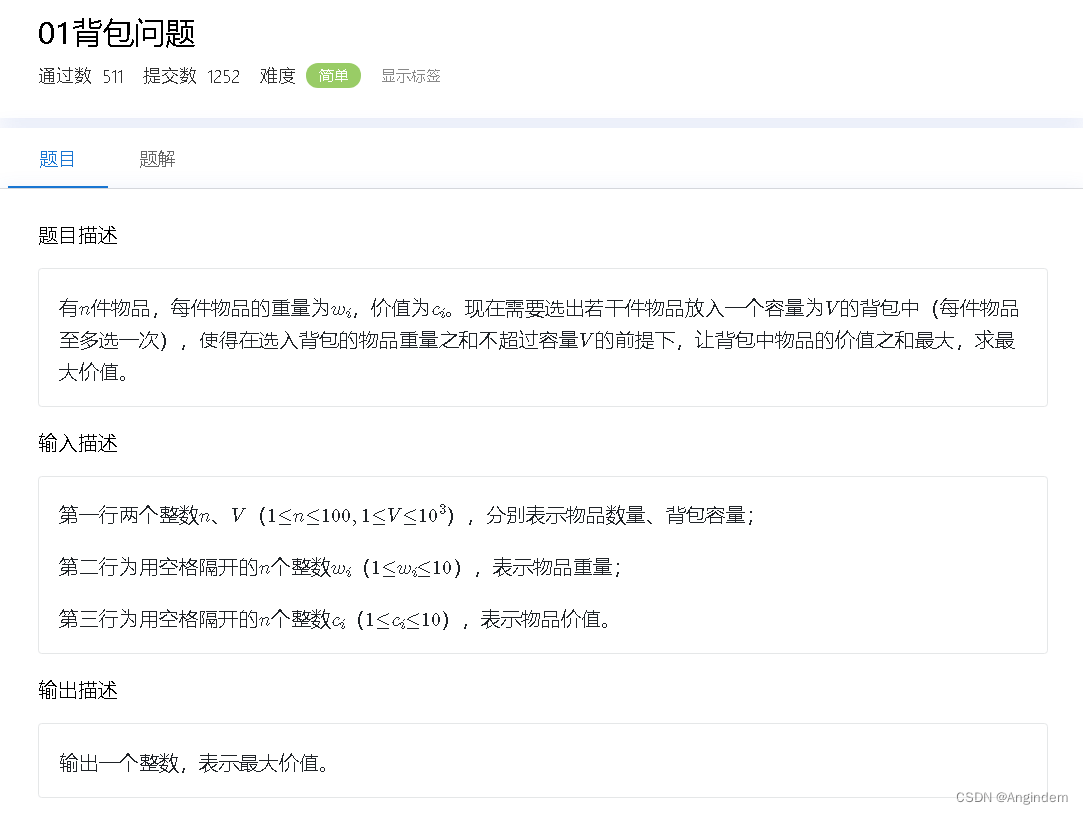

样例：

5 8
3 5 1 2 2
4 5 2 1 3

思路：

? ? ? ? 对于 01 背包问题，我们需要明确 DP 数组的含义，这里 经典的 01 背包问题可以用 二维DP进行表示。

? ? ? ? 即：? dp[ i ][ j ] ,? ?其中? i? ?表示的是 物品编号? j? ?表示背包容量? ?，? dp[ i ][ j ] 表示最大价值

01 背包的递推公式为 ：

dp[i][j] = max ( dp[ i - 1][ j ] , dp[?i - 1 ][ j - w[ i ] ] + c[ i ] );

递推公式的含义是

拿取 i 物品时，背包容量为 j 的时候  =  

max (上一个 物品状态(i - 1)容量为 j 的时候的价值  , 

上一个 物品状态(i - 1)容量为 j 的时候的价值 现在取  当前物品 i 所得到的价值 + c[i] ) 


/*  哪个最大价值 就是取哪个  */

AC代码如下：

#include <iostream>
#include <vector>
#include <queue>
#include <cstring>
#include <algorithm>
#include <unordered_map>
#define endl '\n'
#define int long long
#define YES puts("YES")
#define NO puts("NO")
#define umap unordered_map
#define All(x) x.begin(),x.end()
#pragma GCC optimize(3,"Ofast","inline")
#define IOS std::ios::sync_with_stdio(false),cin.tie(0), cout.tie(0)
using namespace std;
const int N = 2e6 + 10;


inline void solve()
{
	int n,m;
	cin >> n >> m;
	
	vector<int>w(n + 1,0),c(n + 1,0);
	vector<vector<int>>dp(n + 1,vector<int>(m + 1,0));
	
	
	for(int i = 1;i <= n;++i) cin >> w[i];
	for(int i = 1;i <= n;++i) cin >> c[i];
	
	for(int i = 1;i <= n;++i)
	{
		for(int j = m;j >= w[i];--j)
		{
			dp[i][j] = max(dp[i - 1][j],dp[i - 1][j - w[i]] + c[i]);
		}
	}
	cout << dp[n][m] << endl;
}

signed main()
{
//	freopen("a.txt", "r", stdin);
	IOS;
	int _t = 1;
//	cin >> _t;
	while (_t--)
	{
		solve();
	}

	return 0;
}

最后提交：