【卫星定位】GPS/BDS北斗卫星单点定位SPP详解（附Matlab源码）

Abstract

本文使用Matlab编写了支持RINEX 3.03的单点定位系统（Single Point Positioning，SPP)，目前支持GPS与北斗系统定位。具体工作如下：1）实现了RINEX格式的OBS与NAV数据解析程序，通过NAV文件得到观测卫星轨道位置与钟差，通过OBS文件得到卫星观测伪距；
2）实现了对伪距的观测与误差建模，采用最小二乘优化解算，并对HDOP值等估计参数进行了计算；
3）进行了定点基站定位与移动站定位的误差分析，最后解算结果以NMEA 0183格式输出。为贡献卫星学习社区，本文代码将开源于：https://github.com/Franky-X/SPP-Supporting-RENIX3.03-with-GPS-BDS。

Introduction

卫星单点定位系统（Single Point Positioning，SPP)是最常用且简单的定位手段之一。SPP利用接收机收到的广播星历数据解析出各卫星的轨道位置，结合卫星的伪距、钟差以及对流层、电离层误差模型，对接收机位置进行解算。本文针对RENIX
3.03格式接收机数据进行了解析，完成了支持GPS和北斗系统的定位，并分析了定位误差结果。本文的核心工作点如下：

• 实现了OBS与NAV数据解析程序，通过NAV文件得到观测卫星轨道位置与钟差，通过OBS文件得到卫星观测伪距；

• 实现了对伪距的观测与误差建模，采用最小二乘优化解算，并对HDOP值等估计参数进行了计算；

• 进行了定点基站定位与移动站定位的误差分析，并将代码开源至社区。

本文将就以下内容展开介绍。第2部分详细介绍了SPP的整体流程，RENIX文件的读取格式、卫星位置计算以及伪距观测与误差建模的原理。第3部分介绍了SPP算法在Matlab中的实现方式和细节。第4部分展示了GPS和BDS的定位结果与误差分析。第5部分总结了本文的工作内容。

Methods

在本小节，我们首先介绍了SPP定位的系统框架，然后对RENIX文件的NAV和OBS文件读取方法进行了分析，接着我们介绍了GPS和北斗卫星位置的解算方法。最后讨论了伪距观测与误差建模过程，介绍了最小二乘问题的构建与解算。

系统框架

如图所示，SPP定位的主要原理是利用已知的卫星位置，结合观测的伪距与对流层模型进行位置解算。

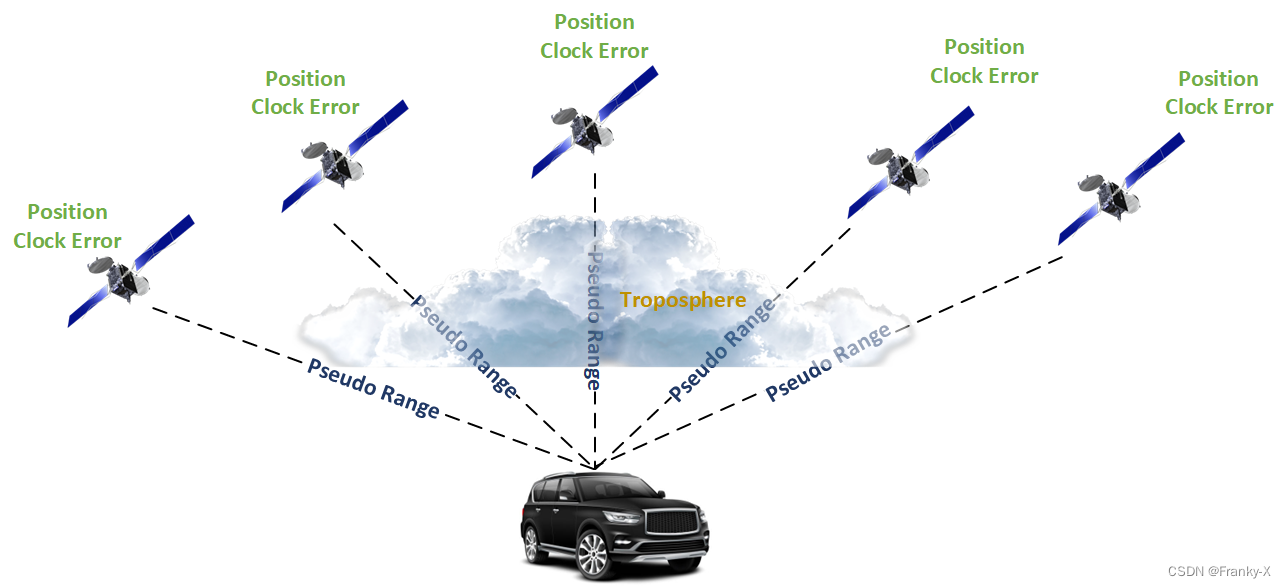
系统执行流程如图所示，首先卫星的位置及钟差由NAV文件读取获得，卫星的伪距观测由OBS文件获得。接着，将卫星的位置、钟差、观测伪距以及对流层误差模型结合，构建最小二乘问题解算，最后输出用户的位置以及相关估计参数。

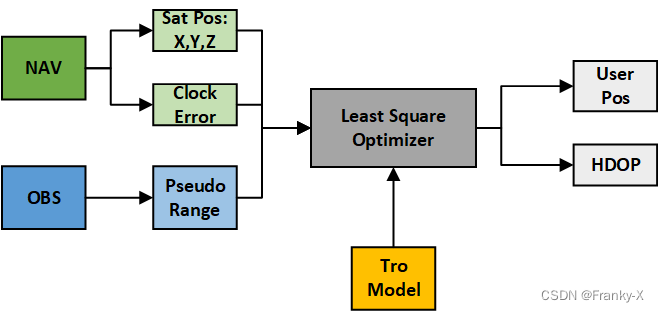
RENIX文件解析

RENIX文件包括了对卫星轨道位置参数的解算和接收机伪距观测的信息提取，接下来进行详细介绍。

NAV文件解析

NAV文件分为头部解释部分和数据部分，其中头部解释Header部分的信息量有限。主要通过数据部分，结合官方RINEX手册中的广播星历解释，获取计算卫星位置和钟差所需要的轨道参数。参数解析方式可参照我的NAV解析代码https://github.com/Franky-X/Computation-of-BD-Orbit，在此不再赘述。

在读取NAV文件时需要记录卫星编号，以便后续在得到伪距观测侯寻找到与之对应的卫星位置与钟差。

OBS文件解析

OBS文件分为头部解释部分和数据部分。其中头部解释Header部分主要描述了卫星系统、接收消息的种类、接收消息的间隔与接收消息的起止时间，对于数据解析非常重要，部分重要字段如表所示。

含义	字段
卫星系统/参数个数/观测种类	SYS / / OBS TYPES
信息时间间隔	INTERVAL
第一次观测时刻（GPS时间）	GPS TIME OF FIRST OBS
最后一次观测时刻（GPS时间）	GPS TIME OF LAST OBS

SPP利用的是伪距进行定位，因此在数据部分我们需要提取的是伪距观测量，在OBS TYPE字段中，伪距观测的首字母为C，因此在读取卫星伪距过程中，只需要读取首字母为C，具有相同波段n的数据即可。
此外，在读取OBS文件过程中，每一个时刻读入的数据记作一个Epoch，便于后续处理。

卫星位置解算

卫星位置和钟差的解算是SPP伪距定位的基础，GPS与北斗系统的卫星系统在真实定位情况中计算有所不同，下面详细介绍GPS和北斗系统的卫星位置与钟差解算过程。

GPS卫星位置解算

计算GPS卫星运动的平均角速度 首先根据广播星历给出的参数 $\sqrt{A}$
计算参考时刻 $t_{oe}$ 的平均角速度 ${\mathrm{n}}_0$ :
$${\mathrm{n}}_0=\frac{\sqrt{GM}}{(\sqrt{A}{)}^3}$$

$G$ 是万有引力常数， $M$ 是地球总质量，$GM=3.986005\times 10^{\wedge }14$ 。
再根据广播星历中给定的摄动参数n’计算观测时刻卫星的平均角速度:
$$n=n_0+n$$

计算观测瞬间的平近点角M $$M=M_0+n\left(t?t_{oe}\right)$$

$\mathrm{M}0$ 为参考时刻 $t_{oe}$ 的平近点角，由广播星历给出。
这里用参考时刻而不用近地点时刻的原因：广播星历每两小时更新一次，将参考时刻设置在中间时刻，则外推时间间隔均小于等于1小时，如果用近地点时刻，外推可能达到6小时。简单模型也可获得精度较高的结果。

计算偏近点角M： 弧度表示的开普勒方程: $$E=M+e\sin E$$

角度表示的开普勒方程:
$$E^{°}=M^{°}+\rho ?e\sin E^{°}$$

计算真近点角： $$\begin{array}{c}\cos f=\frac{\cos E?e}{1?e\cos E}\\ \sin f=\frac{\sqrt{1?e^2}\sin E}{1?e\cos E}\end{array}$$

e为卫星轨道的偏心率，由广播星历给出.
$$f=\arctan \frac{\sqrt{1?e^2}\sin E}{\cos E?e}$$

计算升交角距： $$u^{\prime }=\omega +f$$

$\omega$ 为近地点角距，由广播星历给出。

计算摄动改正项： 广播星历中给出了6个摄动参数:$C_{uc},C_{us},C_{rc},C_{rs},C_{rs},C_{is}$ 可以求出由$\mathrm{J}2$ 项而引起的升交角距u的改正项、卫星矢径 $\mathrm{r}$的改正项和卫星轨道倾角i的摄动改正项 $$\begin{array}{c}{\delta }_u=C_{uc}\cos 2u^{\prime }+C_{us}\sin 2u^{\prime }\\ {\delta }_r=C_{rc}\cos 2u^{\prime }+C_{rs}\sin 2u^{\prime }\\ {\delta }_i=C_{ic}\cos 2u^{\prime }+C_{is}\sin 2u^{\prime }\end{array}$$ 进行摄动改正 $$\begin{array}{c}u=u^{\prime }+{\delta }_u\\ r=u^{\prime }+{\delta }_r=a(1?e\cos E)+{\delta }_r\\ i=i_0+{\delta }_i+\frac{di}{dt}\left(t?t_{oe}\right)\end{array}$$

a为卫星轨道长半径， $\mathrm{i}0$ 为参考时刻 $t_{oe}$的轨道倾角，由广播星历中的开普勒六参数给出， $\mathrm{di}/\mathrm{dt}$
为i的变化率，由广播星历中的摄动九参数给出。

计算卫星在轨道面坐标系中的位置：
轨道平面直角坐标系中（坐标原点位于地心，X轴指向升交点）卫星的平面直角坐标系：
$$\begin{array}{rl}& \mathrm{x}=r\cos u\\ & y=r\sin u\end{array}$$

计算观测瞬间升交点的经度 $L$：若参考时刻 $t_{oe}$ 时升交点赤经为${\Omega }_{t_{oe}}$ ，升交点对时间的变化率为 $\dot{\Omega }$
（从广播星历的摄动参数中给出），则观测瞬间暏升交点赤经为:
$$\Omega ={\Omega }_{t_{oe}}+\dot{\Omega }\left(t?t_{oe}\right)$$

${\omega }_e=7.292115\times 10^{\wedge }?5\mathrm{rad}/\mathrm{s}$，为地球自转速度； $\mathrm{t}$ 为周内秒，假设地球自转为完全匀速，则
$$\begin{array}{c}L=\Omega ?GAST={\Omega }_{t_{oe}}?GAS{T}_{week}+\dot{\Omega }\left(t?t_{oe}\right)?w_{e}t\\ ={\Omega }_0+\left(\dot{\Omega }?w_e\right)t?\dot{\Omega }{t}_{oe}\end{array}$$

广播星历中给出的 ${\Omega }_0$ ， 即与本周开始时刻之差。

计算卫星在ECEF坐标系中的位置 通过两次旋转求解 $$\begin{array}{c}\left(\begin{array}{l}X\\ Y\\ Z\end{array}\right)=R_z(?L)R_X(?i)\left(\begin{array}{l}x\\ y\\ 0\end{array}\right)\\ =\left(\begin{array}{c}x\cos L?y\cos i\sin L\\ x\sin L+y\cos i\cos L\\ y\sin i\end{array}\right)\end{array}$$

最后，计算卫星钟差： $$\begin{array}{c}\Delta t=Tsv?toc\\ dtr=F?e?sqrtA?\sin E\\ \text{sat\_Clk\_error}=a{f}_2?\Delta t^2+a{f}_1?\Delta t+a{f}_0+dtr\end{array}$$

北斗卫星位置解算

对于北斗卫星的位置解算，流程与GPS大致相同。但是，值得注意的时，北斗卫星的时间要比GPS时间快14秒，由于在NAV文件中时间基准为GPS，所以这一个时间偏移在北斗卫星位置计算中非常重要。因此，需要在计算$t_k$时，额外减去14秒的偏移，即
$$tk=Tsv?toe?14$$
另外，与GPS不同的是，北斗卫星分为MEO/IGSO卫星和GEO卫星，其中MEO/IGSO卫星的计算与GPS卫星相同，但是GEO卫星的位置需要额外的变换[@b3]。GEO卫星的计算过程如下

首先进行所需参数计算 $$\begin{array}{rl}& f=\frac{?5}{180}\pi \\ & p=\dot{\Omega }?tk\end{array}$$

然后对MEO/IGSO卫星的计算结果进行旋转变换： $$\begin{array}{rl}& Rx=\left[\begin{array}{ccc}1& 0& 0\\ 0& \cos f& \sin f\\ 0& ?\sin f& \cos f\end{array}\right]\\ & Rz=\left[\begin{array}{ccc}\cos p& \sin p& 0\\ ?\sin p& \cos p& 0\\ 0& 0& 1\end{array}\right]\\ & \left[\begin{array}{l}\mathrm{GEOX}\\ \mathrm{GEOY}\\ \mathrm{GEOZ}\end{array}\right]=Rz?Rx?\left[\begin{array}{l}X\\ Y\\ Z\end{array}\right]\end{array}$$

伪距观测与误差建模

SPP算法核心就是伪距的观测方程与误差建模，接下来介绍SPP最小问题的构建和相关不确定值得计算。

最小二乘问题构建

首先，我们需要对伪距观测进行建模，单点伪距得观测如下：
$$\begin{array}{c}\tilde{\rho }=\sqrt{{\left(X^S?X\right)}^2+{\left(Y^S?Y\right)}^2+{\left(Y^S?Y\right)}^2}\\ +C?dt?C?dT+{\delta }_{atmos}\end{array}$$
其中，$\tilde{\rho }$为伪距观测值，$\left(X^S,Y^S,Z^S\right)$为卫星位置，$(X,Y,Z)$为需要估计得测站坐标，$dt$为接收机钟差，$dT$为卫星钟差，${\delta }_{\text{atmos?}}$
为大气引起的误差。

接下来使用泰勒公式对伪距观测进行线性化。首先我们定义：
$$R_0=\sqrt{{\left(X^S?X_0\right)}^2+{\left(Y^S?Y_0\right)}^2+{\left(Z^S?Z_0\right)}^2}$$
接着，若不计大气误差，我们在初始值点对伪距观测进行近似：
$$\begin{array}{c}\tilde{\rho }\approx \sqrt{{\left(X^S?X_0\right)}^2+{\left(Y^S?Y_0\right)}^2+{\left(Z^S?Z_0\right)}^2}+Cd{t}_0\\ +{\frac{?\tilde{\rho }}{?X}|}_{X_0}\Delta X+{\frac{?\tilde{\rho }}{?Y}|}_{Y_0}\Delta Y+{\frac{?\tilde{\rho }}{?Z}|}_{Z_0}\Delta Z+\frac{?\tilde{\rho }}{?(Cdt)}\Delta (Cdt)\end{array}$$ 对于每个变量的偏导数，我们记为：
$$l=?\frac{X^S?X_0}{R_0}m=?\frac{Y^S?Y_0}{R_0}n=?\frac{Z^S?Z_0}{R_0}$$
于是，伪距观测可以表示为：
$${\tilde{\rho }}^n\approx R_0^n+Cd{t}_0+l^n?\Delta X+m^n?\Delta Y+n^n?\Delta Z+\Delta (Cdt)$$
记伪距观测的误差为为
$$v_n=R_0{}^n+Cd{t}_0+l^n?\Delta X+m^n?\Delta Y+n^n?\Delta Z+\Delta (Cdt)?{\tilde{\rho }}^n$$
因此，我们可以构建如下的最小二乘问题： $$\begin{array}{c}\left[\begin{array}{c}{v}_1\\ v_2\\ ?\\ v_n\end{array}\right]=\left[\begin{array}{cccc}{l}^1& m^1& n^1& 1\\ l^2& m^2& n^2& 1\\ & ?& & \\ l^n& m^n& n^n& 1\end{array}\right]\left[\begin{array}{c}\Delta X\\ \Delta Y\\ \Delta Z\\ \Delta (Cdt)\end{array}\right]\\ +\left[\begin{array}{c}{R}_0{}^1+Cd{t}_0?{\tilde{\rho }}^1\\ R_0{}^1+Cd{t}_0?{\tilde{\rho }}^1\\ ?\\ R_0{}^n+Cd{t}_0?{\tilde{\rho }}^n\end{array}\right]\end{array}$$ 可记为 $$\mathbf{V}=\mathbf{HX}+\mathbf{B}$$
最后只需要使用非线性最小二乘法对该问题迭代求解即可。

HDOP值计算

在SPP中，为了评估解算不确定度，定义了精度因子指标。其中，水平精度因子HDOP反映了SPP在水平X,Y方向的估计定位精度。HDOP的计算与最小二乘的迭代方差有关，定义：
$$\mathbf{G}={\left({\mathbf{H}}^T\mathbf{H}\right)}^{?1}=\left[\begin{array}{lll}{G}_{xx}& G_{xy}& G_{xz}\\ G_{yx}& G_{yy}& G_{yz}\\ G_{zx}& G_{zy}& G_{zz}\end{array}\right]$$

$\mathbf{G}$实际上就表示了最小二乘迭代最后结果的方差，HDOP的定义为：
$$\mathrm{HDOP}=\sqrt{G_{xx}+G_{yy}}$$ HDOP值的范围在[0.5, 99]之间，HDOP值越小，代表定位估计精度越高。

Implementation Details

本小节介绍了SPP算法的Matlab实现，从RINEX文件读取，最小二乘问题构建以及求解结果输出介绍了SPP的实现细节。

RINEX文件读取

首先，对NAV文件读取需要跳过Header部分，并寻找所需卫星系统的广播星历，读取相应轨道参数，将卫星编号和摄动参数对应存储。读取NAV文件的核心代码如下：

    while ~feof(fileID)
        line = fgets(fileID);
        line_cnt = line_cnt + 1;
        if line_cnt > 5
            if contains(line, 'C')  % C for BDS and G for GPS
                readstate = 1;
                index_buf(end+1) = str2double(line(2:3));
                tmp_data = str2num(line(4:end));
            end
            if readstate == 1
               eph_cnt = eph_cnt + 1;
               tmp_data = [tmp_data str2num(line)];
               if eph_cnt == 8
                   eph_buf(:,end+1) = tmp_data;
                   readstate = 0;
                   eph_cnt = 0;
               end
            end
        end
    end

对应NAV文件读取星历参数的数据结构如图所示。

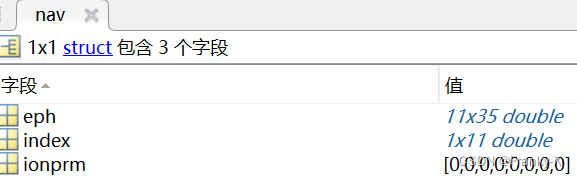
其中eph存储了卫星的广播星历参数，index存储了对应卫星的编号，由于所用NAV文件没有电离层参数信息，因此ionprm为空。
对于OBS文件的读取，流程更加复杂。首先，需要从Header部分读取时间、卫星系统以及观测系统的数据格式等信息。接着，需要在数据部分读取对应卫星系统的观测，并且记录卫星编号及其对应epoch。读取OBS文件的核心代码如下所示：

    while ~feof(fileID)
        line = fgets(fileID); 
        if contains(line, 'TIME OF FIRST OBS')
            dateStr = strtrim(line(1:end-35)); 

            date = str2num(dateStr);
        end
        if contains(line, 'APPROX POSITION XYZ')
            rcvpos = str2num(line(1:end-22));
        end
        if contains(line, 'SYS / # / OBS TYPES')
            sysStr = strtrim(line(1)); 
            numStr = strtrim(line(6));
            num = str2double(numStr);
            typeStr = strtrim(line(7:7+num*4)); 
            cellArray = strsplit(typeStr, ' ');
            if sysStr == 'C'  % C for BDS, G for GPS
                type = cellArray';
            end
        end
        if contains(line, '>')
            read_state = 1;
            if epoch_cnt == -1
                epoch_cnt = epoch_cnt + 1
            else
                epoch_cnt = epoch_cnt + 1; %v2 30
            end
        end
        if read_state == 1 && ~contains(line, '>')
            sysStr = strtrim(line(1));
            if sysStr == 'C' 
                epoch_buf(end+1) = epoch_cnt;
                index_buf(end+1) = str2double(line(2:3));
       
                tmp = nan(1,9);
                tmp_data = str2num(line(4:end));
                tmp(1:length(tmp_data)) = tmp_data;
                data_buf(end+1,:) = tmp;
            end
        end
    end
    epoch = epoch_buf';
    index = index_buf';
    data = data_buf;
    fclose(fileID); 
    return;

对应OBS文件的数据结构如图

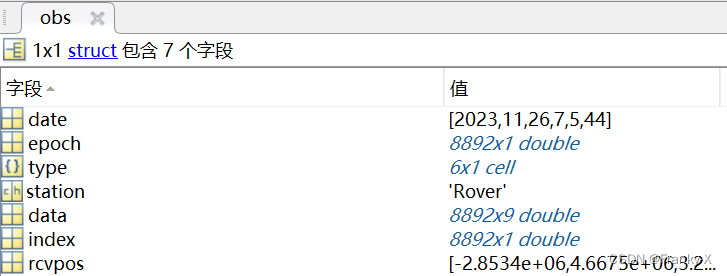
其中date中包含了观测的时间，epoch包含每个历元所在的观测时间，type中存储了观测种类，station为测站名称，data存储了观测数据，index存储了卫星编号，rcvpos为定位估计位置。

卫星位置与钟差解算

卫星位置与钟差解算与作业一中类似，但是针对北斗卫星，需要进行特殊处理。例如，对时钟对齐GPS的校正，卫星分类计算。为了简洁，在报告只展示了北斗卫星的位置与钟差解算，解算核心代码如下所示。

    A = roota*roota;
    half_week = 302400;
    tk = SOW-toc-14;
    if tk >  half_week, tk = t-604800; end
    if tk < -half_week, tk = t+604800; end
    tcorr = (af2*tk + af1)*tk + af0;
    n0 = sqrt(GM/A^3);
    n = n0+deltan;
    M = M0+n*tk;
    M = rem(M+2*pi,2*pi);
    E = M;
    for i = 1:10
       E_old = E;
       sinE=sin(E);
       E = M+ecc*sinE;
       dE = rem(E-E_old,2*pi);
       if abs(dE) < 1.e-12
          break;
       end
    end
    E = rem(E+2*pi,2*pi);
    cosE=cos(E);

    dtr = F * ecc * roota * sinE;
    v = atan2(sqrt(1-ecc^2)*sinE, cosE-ecc);
    phi = v+omega;
    phi = rem(phi,2*pi);

    cos2phi=cos(2*phi);
    sin2phi=sin(2*phi);

    u = phi		         + cuc*cos2phi+cus*sin2phi;
    r = A*(1-ecc*cosE) + crc*cos2phi+crs*sin2phi;
    i = i0+idot*tk	      + cic*cos2phi+cis*sin2phi;

    x1 = cos(u)*r;
    y1 = sin(u)*r;
    if svprn>5%IGSO/MEO
        Omega = Omega0+(Omegadot-Omegae_dot)*tk-Omegae_dot*toe;
        dOmega = Omegadot - Omegae_dot;
         Omega = rem(Omega+2*pi,2*pi);

        satpos(1,1) = x1*cos(Omega)-y1*cos(i)*sin(Omega);
        satpos(1,2) = x1*sin(Omega)+y1*cos(i)*cos(Omega);
        satpos(1,3) = y1*sin(i);
        
    else%GEO
        Omega = Omega0 + (Omegadot-0)*tk - Omegae_dot*toe;
        dOmega = Omegadot-0;
        %Reduce to between 0 and 360 deg
        Omega = rem(Omega+2*pi,2*pi);
        % Compute satellite coordinates
        x_gk = x1 * cos(Omega) - y1 * cos(i)*sin(Omega);
        y_gk = x1 * sin(Omega) + y1 * cos(i)*cos(Omega);
        z_gk = y1 * sin(i);
        ang0=-5/180*pi;

        Rx=[1 0 0; 0 cos(ang0) sin(ang0);0 -sin(ang0) cos(ang0)];
        Rz=[cos(Omegae_dot*tk) sin(Omegae_dot*tk) 0;-sin(Omegae_dot*tk) cos(Omegae_dot*tk) 0;0 0 1];
        satpos=Rz*Rx*[x_gk,y_gk,z_gk]';
        satpos=satpos';
            
    end
    satclock=tcorr+dtr-tgd;

首先，对于tk的计算，需要减去14秒以统一至GPS时钟基准，在最后的卫星位置解算时，需要对PRN小于5的IGSO/MEO卫星与PRN大于等于5的GEO卫星进行解算。GPS的计算相对简单，只是北斗卫星位置与钟差计算的一个部分，不需要额外的时间校正与分类计算，在此不再赘述。

最小二乘问题构建

最小二乘问题的构建需要结合伪距观测，卫星位置以及钟差进行迭代求解。首先，在一个历元中，需要匹配OBS中的卫星编号与NAV文件中的卫星编号，代码如下所示

        eph_t = find(obs.epoch == (i-1));     % Check time        
        PRN   = obs.index(eph_t);             % Check satellite number (PRN)

        if length(PRN)< 4; continue;end
            
        % Second Of Day
        SOD = obs.epoch(eph_t)+((obs.date(4)*60*60)+(obs.date(5)*60)+obs.date(6));

        %% 2. Read pseudorange from Observation file
        % Pseudorange
        C1 = obs.data(eph_t,ismember(obs.type,'C2I'));

        
        %% 3. Calculate satellite position and satellite clock bias (For loop#2)
        satpos        = nan(3,length(PRN));
        satclock      = nan(length(PRN),1);
        for ii = 1:length(PRN)
            [satpos(1:3,ii),satclock(ii)] = satpos_xyz_sbias(SOD(ii),...
            PRN(ii),nav.eph,nav.index,obs.date,C1(ii));
        end
            
        if length(satclock(~isnan(satclock))) < 4;continue;end % Check number of satellite

在匹配卫星后，还需要检查卫星数目是否足够，至少需要4颗卫星才能进行位置和接收机钟差解算，如果小于4颗卫星，那么直接跳过这个历元。

在得到相应观测与卫星位置与钟差后，需要构建设计矩阵，在构建过程中，首先进行仰角15度的卫星进行去除，然后对伪距进行卫星钟差修正。最后构建设计矩阵，迭代求解。核心代码如下所示。

    while norm(dx) > 10^-4 % Difference of positioning
        stop = stop+1; if stop==30;break;end % iterative divergent
        % Calculate elevation angle
        [elev,~] = calelevation(satpos,xyz0);
        userlla  = xyz2lla(xyz0(1),xyz0(2),xyz0(3));
                       
        % Troposheric delay (Tropo model)
        [d_hyd,d_wet] = EstimateTropDalay(userlla(1),userlla(3),str2double(doy));
        delay.tropo = (d_hyd + d_wet).*(1.001./sqrt(0.002001 + sind(elev).^2));
              
        % Ionospheric delay (Klobuchar model) (For loop#3)
        for ii = 1:length(PRN) 
             dIon_klob(ii) = klobuchar_model(userlla(1),userlla(2),elev(ii),SOD(ii),nav.ionprm); % nano sec  newklob nav.ionprm
        end
        delay.iono = c.*dIon_klob;  % delay from Klobuchar model

        % elevation angle cutoff 15 degree
       if stop > 1
            elev_m          = elevcut(elev',elev',elev_mask);
            C1_m            = elevcut(C1',elev',elev_mask);
            satpos_m        = elevcut(satpos,elev',elev_mask);
            sclockbias_m    = elevcut(satclock',elev',elev_mask);
            d_tropo         = elevcut(delay.tropo',elev',elev_mask);
            d_iono          = elevcut(delay.iono',elev',elev_mask);
            PRN_m           = elevcut(PRN',elev,elev_mask);
        else
            delay.tropo     = 0.*elev;
            delay.iono      = 0.*elev;
            elev_m          = elevcut(elev',elev',0);
            C1_m            = elevcut(C1',elev',0);
            satpos_m        = elevcut(satpos,elev',0);
            sclockbias_m    = elevcut(satclock',elev',0);
            d_tropo         = elevcut(delay.tropo',elev',0);
            d_iono          = elevcut(delay.iono',elev',0);
            PRN_m           = elevcut(PRN',elev,0);
        end
                
        cP1 =   nan(1,length(C1_m));     
        % Pseudorange correction
        if length(cP1)~=length(sclockbias_m);break;end % Check number of satellite
        if mode == 1 % No atmospheric delay correction
            cP1 =   C1_m + c.*sclockbias_m;
        end
        if mode == 2 % Ionospheric delay correction
            cP1 =   C1_m + c.*sclockbias_m - d_iono;
        end
        if mode == 3 % Tropospheric delay correction
            cP1 =   C1_m + c.*sclockbias_m - d_tropo;
        end
        if mode == 4 % Tropospheric+Ionospheric delay correction
            cP1 =   C1_m + c.*sclockbias_m - d_tropo - d_iono;
        end
        % remove outlier
        ctest = sqrt( sum((refpos(:)*ones(1,length(satpos_m),1) - satpos_m).^2)); %Ref distance
        cError = cP1-ctest;
        cP1(abs(cError)>1000) = [];
        satpos_m(:,abs(cError)>1000) = [];
        if length(satpos_m) < 4 || length(C1_m) < 4 || length(C1_m)~=length(satpos_m);break;end % Check number of satellite
                
        length(C1_m)
        % Satellite Flight Correction with bc and clock error (SACNAG)     
        satpos_cor = nan(3,length(satpos_m));
        
        for iii = 1:length(satpos_m)
            dtflight = (cP1(iii)-br)/c + sclockbias_m(iii); % + d_iono/c
            satpos_cor(:,iii) = FlightTimeCorr(satpos_m(:,iii),dtflight); % REF
        end   
       
        % Calculate line of sight vectors and ranges from satellite to xo
        v = xyz0(:)*ones(1,length(satpos_cor),1) - satpos_cor;
        range = sqrt( sum(v.^2) );
        v = v./(ones(3,1)*range); % line of sight unit vectors from sv to xo
            
        % Calculate the a-priori range residual
        prHat = range(:) + br;
        P = cP1' - prHat;                    % matrix P
        H = [v',ones(length(satpos_cor),1)]; % matrix H
        
        % LSE solution    
        dx = inv(H'*H)*H'*P;
        
        % update xyz0 and br
        xyz0 = xyz0(:)+dx(1:3);
        br   = br+dx(4);
        
    end

    G = inv(H'*H);
    HDOP = sqrt(G(1,1) + G(2,2));

在解算过程中，还加入了对流层延迟误差模型，电离层模型由于缺少参数不参与计算。在计算之前，还对明显的误差外点进行了剔除，对于距离估计大概位置过远的卫星进行了剔除。在迭代完成后，还对HDOP值进行了计算。

求解结果输出

求解结果以标准文件NMEA 0183格式输出，NMEA格式中的GPGGA语句包含了以下核心字段：

• 经纬度及半球标识符；

• 高程；

• HDOP；

• UTC时间；

• 定位质量（均为单点定位）；

• 使用的卫星数量；

• 校验和。

其中校验和即对语句数据进行1的补码和运算，累加的结果再取反码即生成了检验码。将检验码放入检验和字段中。实现代码如下：

    function checksum = calculateNMEAChecksum(sentence)
        checksum = 0;
        for i = 2:length(sentence) 
            checksum = bitxor(checksum, double(sentence(i)));
        end
        checksum = dec2hex(checksum, 2);
        if length(checksum) < 2
            checksum = ['0', checksum]; 
        end
    end

将最小二乘的结果与相应时间输出为GPGGA格式的字符串形式，并计算校验和，最后输出整段GPGGA语句。

Experimental Results and Discussions

本小节进行了SPP的固定站与移动站、GPS与北斗系统定位实验，并进行了误差分析与相关讨论。

实验系统构建

本实验采用的固定站为微电子楼楼顶天线位置，进行了24+小时观测，有利于误差分析。移动站绕电院草坪绕行，进行了15min的观测，有利于验证SPP算法的移动定位性能。固定站与移动站真值如图所示。

对于GPS系统，我们使用"C1C"伪距进行观测，对于BDS系统，我们使用"C2I"伪距进行观测。

定位结果分析

固定站分析

对于固定站分析我们分别对所实现的GPS和BDS的SPP定位进行了结果分析。

GPS：首先，我们对GPS系统对固定站的定位结果进行了分析，图[为经过对流层误差校正的定位结果，其50%的分布误差在2.282m，符合SPP的整体定位精度量级。

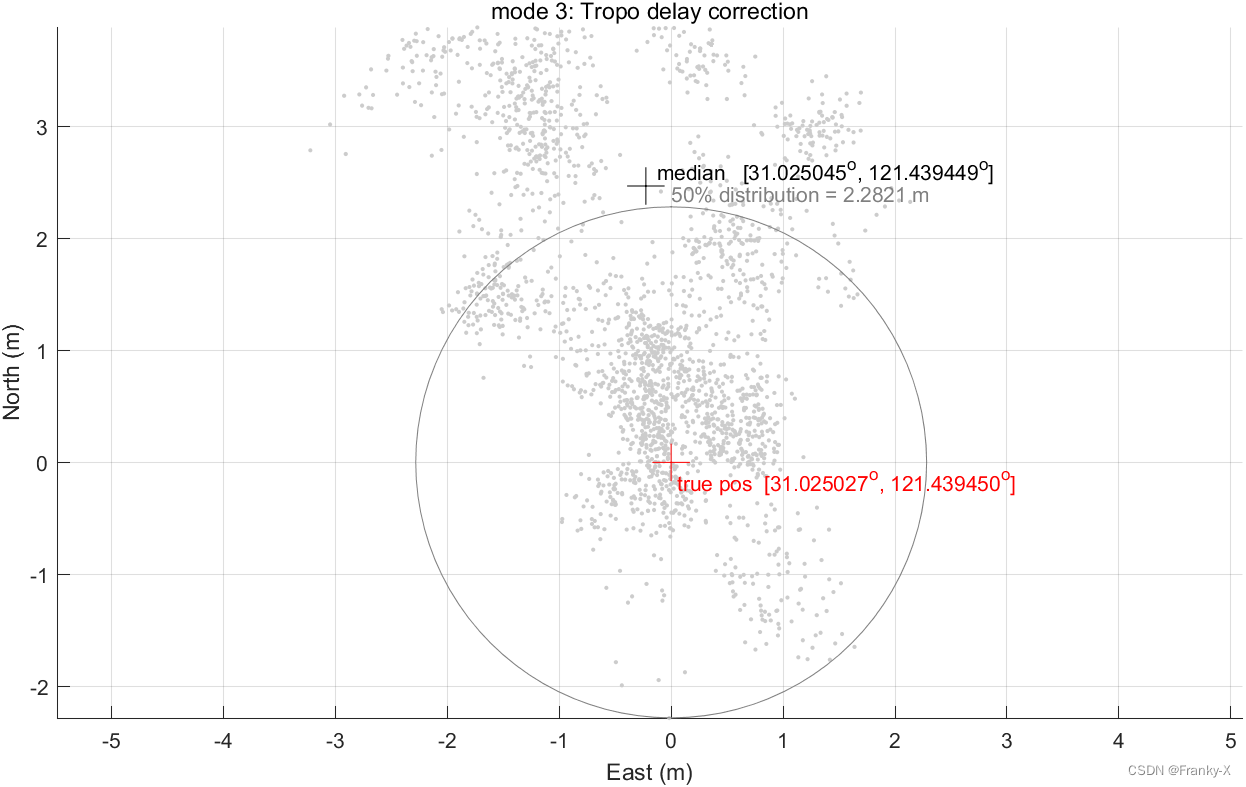
接着，我们对固定站定位的水平和垂直误差随时间的变化进行了分析，如图所示。总体来说水平误差比垂直误差低很多，这符合课程学习的知识。

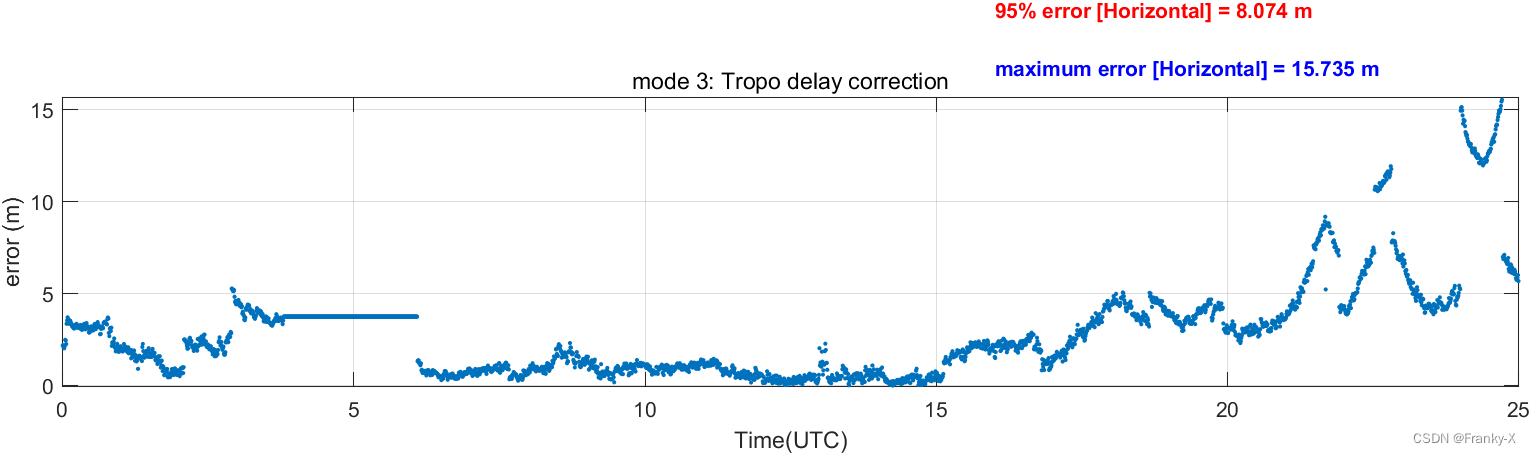
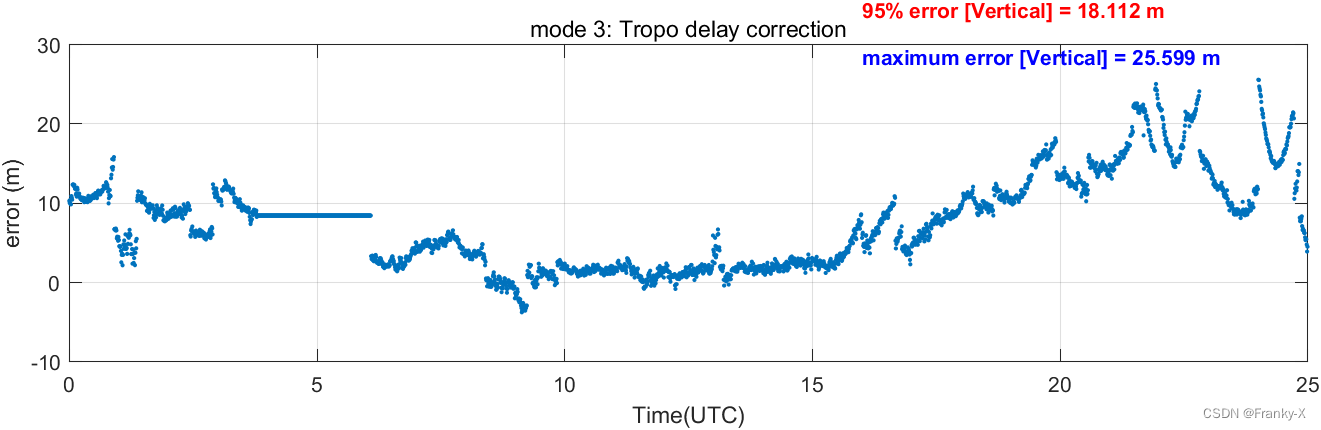
固定站的GPS天空图如图所示，GPS卫星数量丰富且观测条件较好。

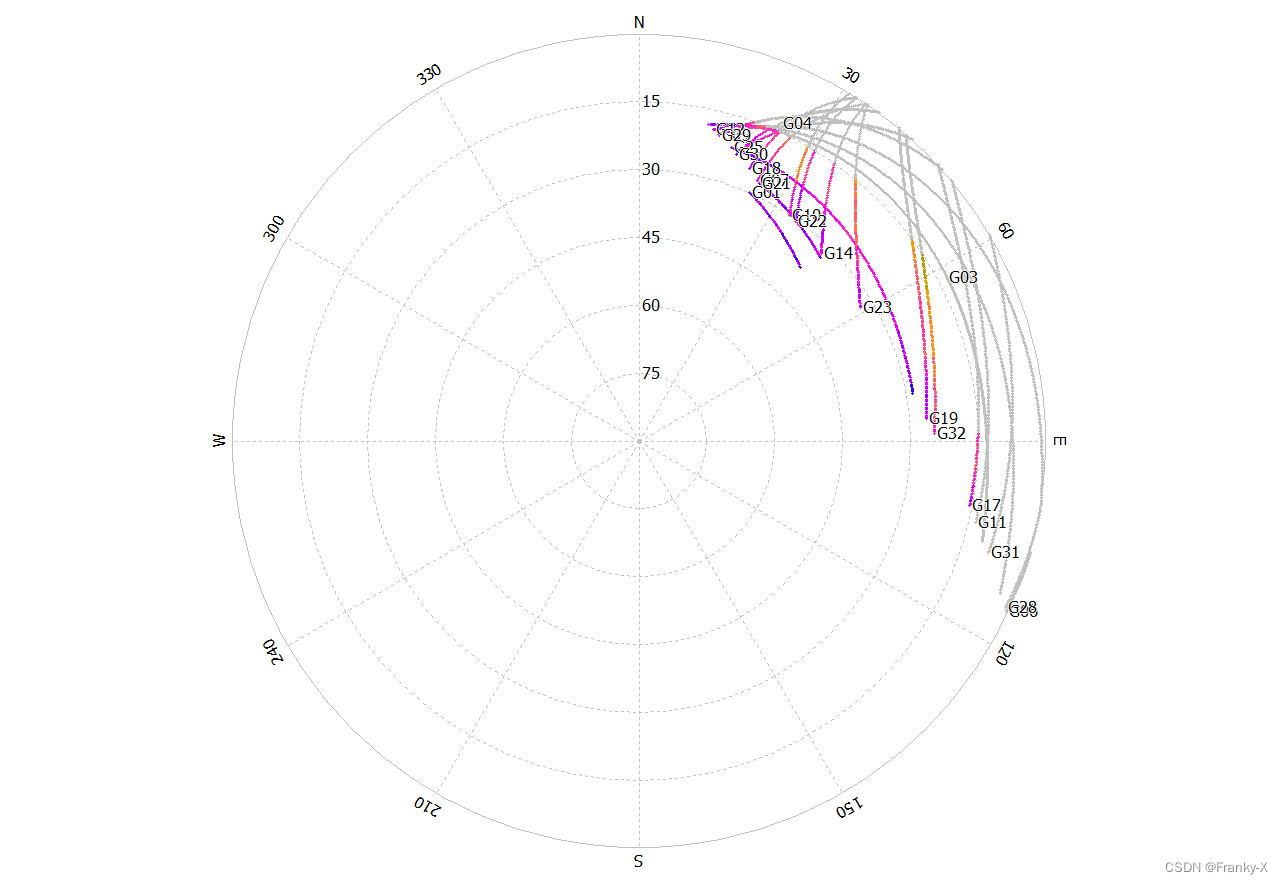
在6-15小时内，水平定位误差最小。进一步，我们分析了卫星在这总观测25h内的可见性。如图所示，在6-15小时内，可见的卫星数目最多，因此定位效果最好，在20个小时以后，可观测到的GPS卫星很好。因此当可见卫星越多时，GPS的定位效果越好。

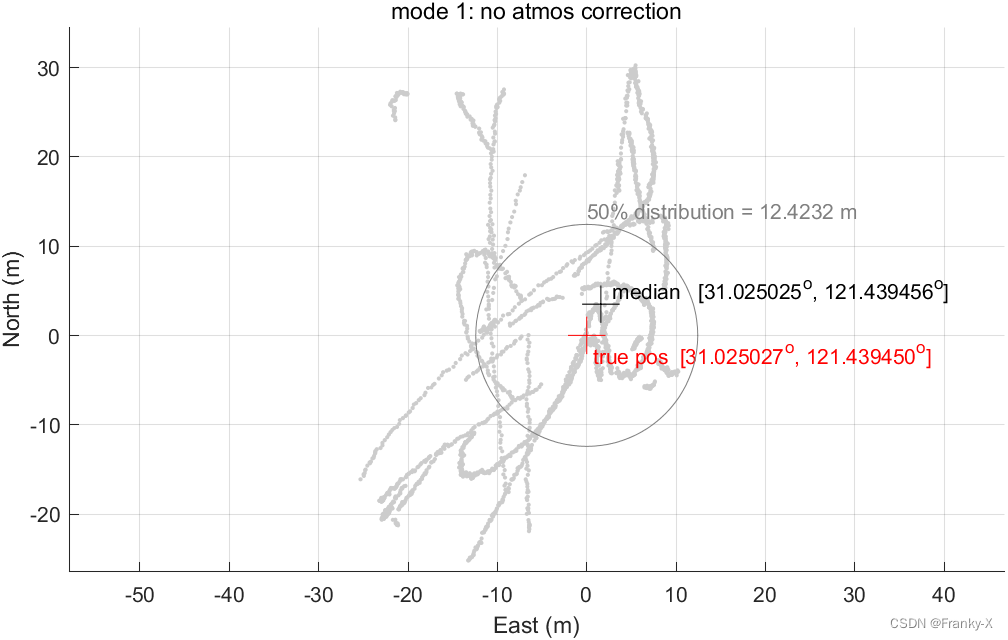
BDS：接着，我们对BDS系统对固定站的定位结果进行了分析，图为无大气误差定位结果，其50%的分布误差在12.423m，符合SPP的整体定位精度量级。相较于GPS，BDS定位精度较低，这是由于BDS的广播星历计算卫星位置不够准确且卫星观测条件较差。BDS的卫星种类与位置解算方法相比GPS非常复杂，并且在广播星历上，BDS确实没有GPS精准。本报告的算法也没有针对BDS特别进行筛星融合等处理，因此BDS卫星的定位精度较低。

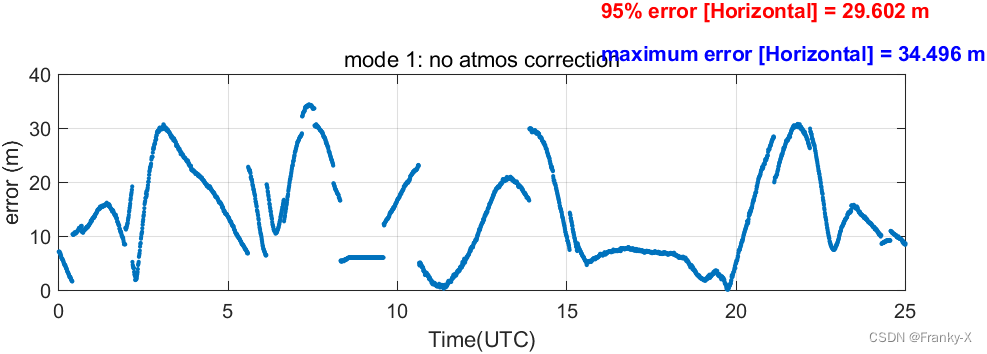
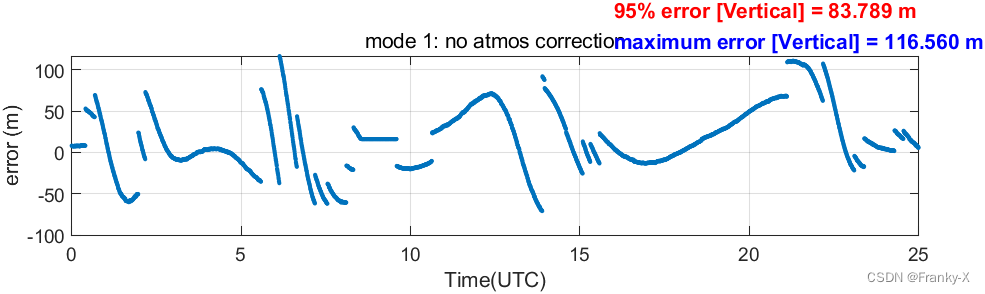
接着，我们对固定站BDS定位的水平和垂直误差随时间的变化进行了分析，如图所示。总体来说水平误差比垂直误差低很多，这符合课程学习的知识。

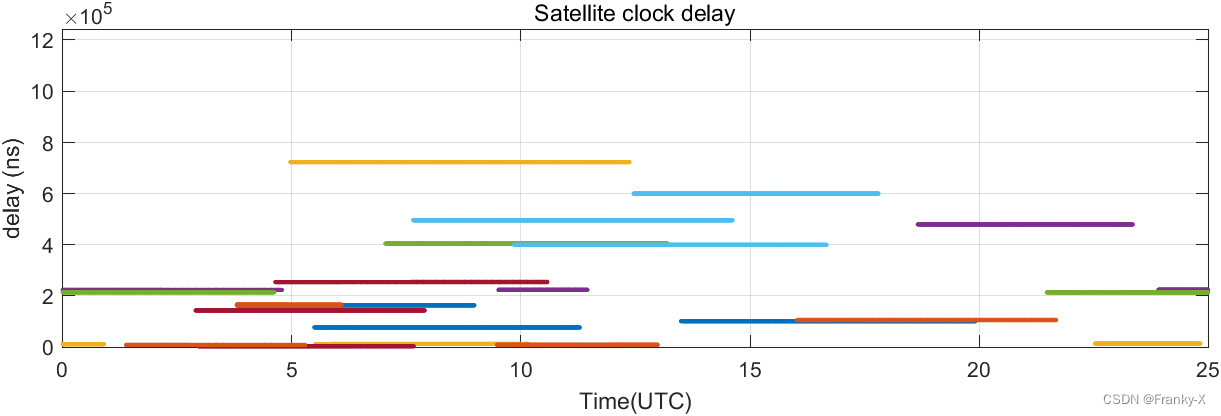
固定站的BDS天空图如图所示，BDS卫星的观测条件较差。

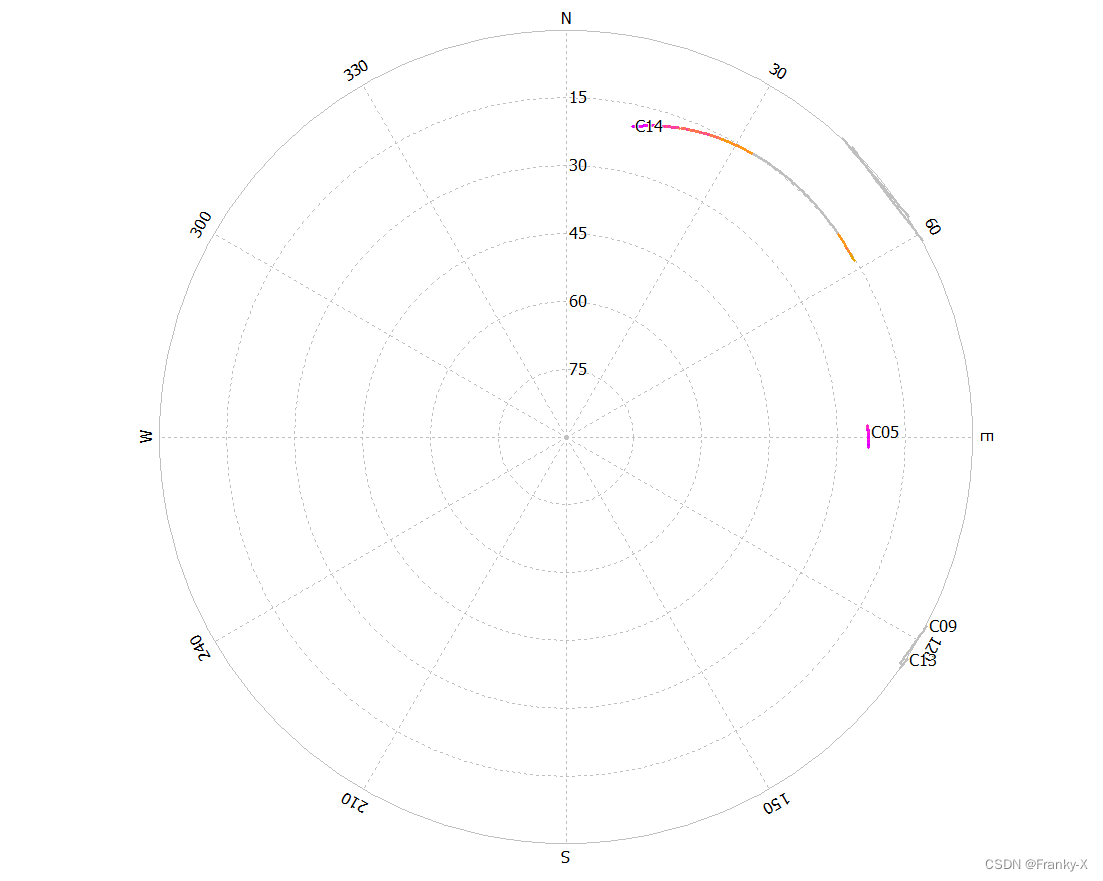
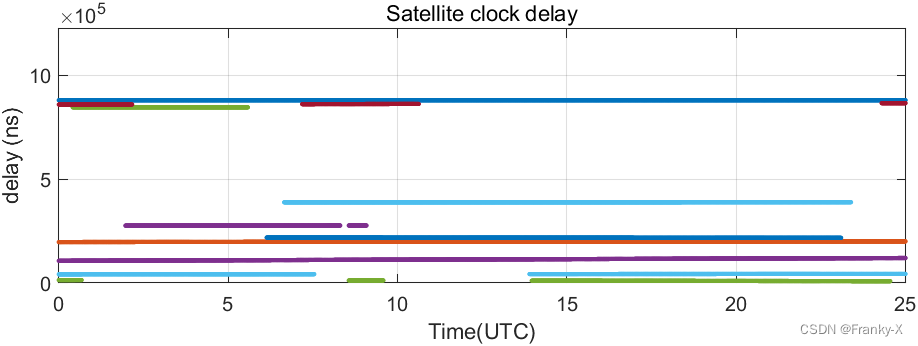
进一步，我们分析了卫星在这总观测25h内的可见性。如图所示，虽然BDS颗可见卫星比GPS多，但是卫星质量较差，因此定位精度较低。若想继续优化BDS定位结果，可以通过筛星等方法，提升参与定位的卫星质量。

移动站分析

对于移动站分析我们分别对所实现的GPS和BDS的SPP定位进行了轨迹对比及结果分析，根据要求，我们输出的轨迹为NMEA格式，本小节将NMEA格式的求解结果导入rtkplot中进行分析，而不是用rtklib求解。

GPS：首先，我们对GPS系统对移动站的定位结果进行了分析，图[为经过对流层误差校正的轨迹结果.

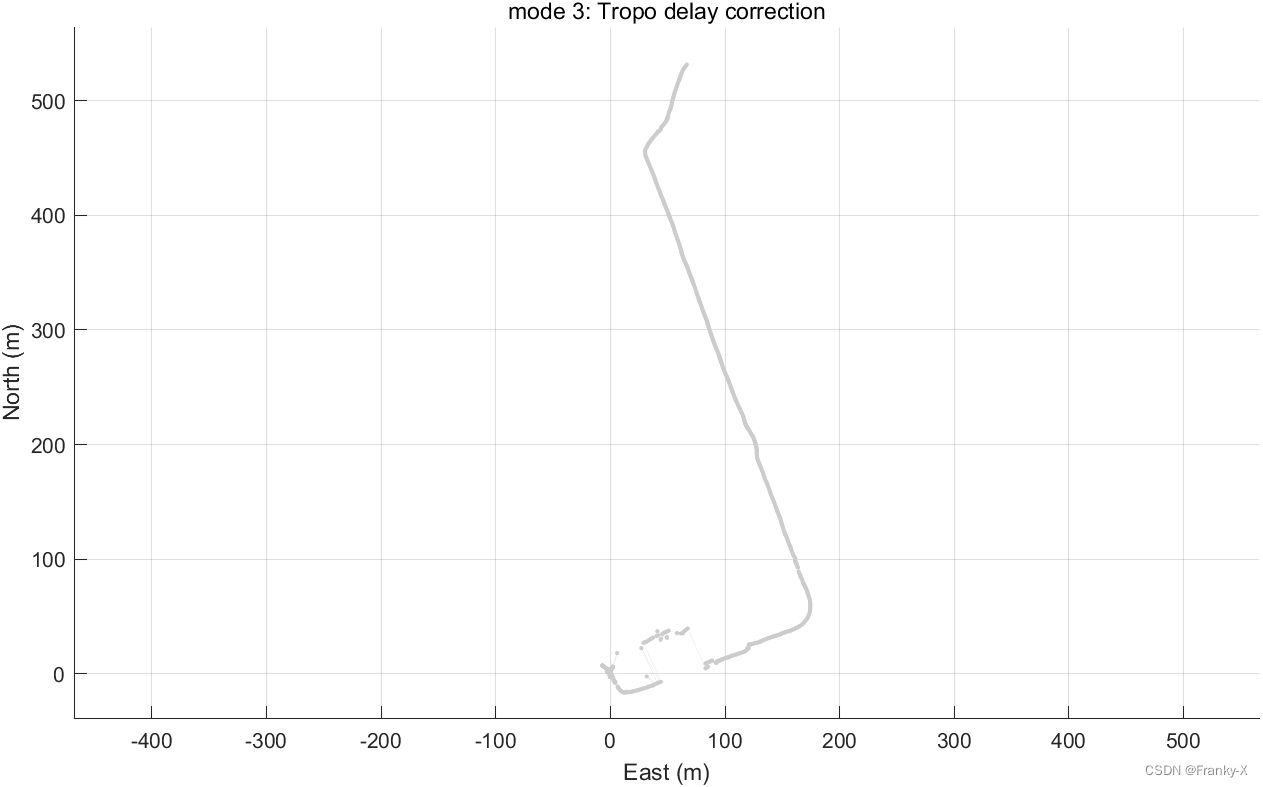
进一步，我们对GPS移动站的定位结果，NMEA格式文件导入RTKPLOT中，同时将参考真值的轨迹文件也导入RTKPLOT中进行比较。如图，GPS的移动站定位结果在水平方向上为15m左右，其中在7:10-7:13时间段，误差达到40m，在垂直方向上的定位误差在20m左右，与SPP定位精度量级一致。

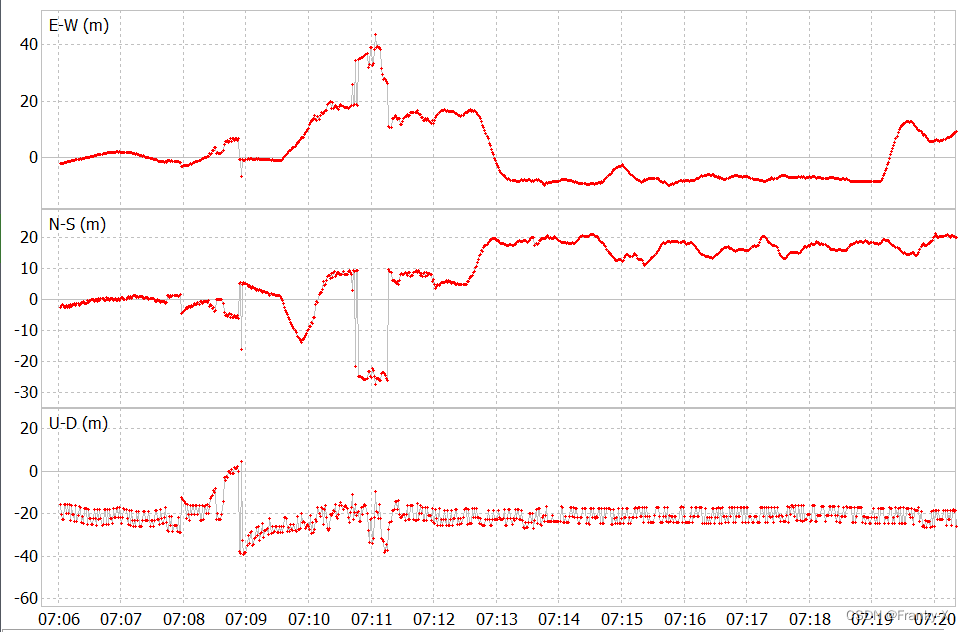
进而，我们分析了GPS的移动站可见性，如图14{reference-type=“ref”
reference=“fig:GPS_Rover_SV”}所示，移动站的GPS卫星可见性与固定站相比较差，卫星数目较少，特别在7:10-7:13时间段，卫星数目极少，导致定位漂移很大。

BDS：我们对北斗系统对移动站的定位结果进行了分析，图为经过对流层误差校正的轨迹结果。

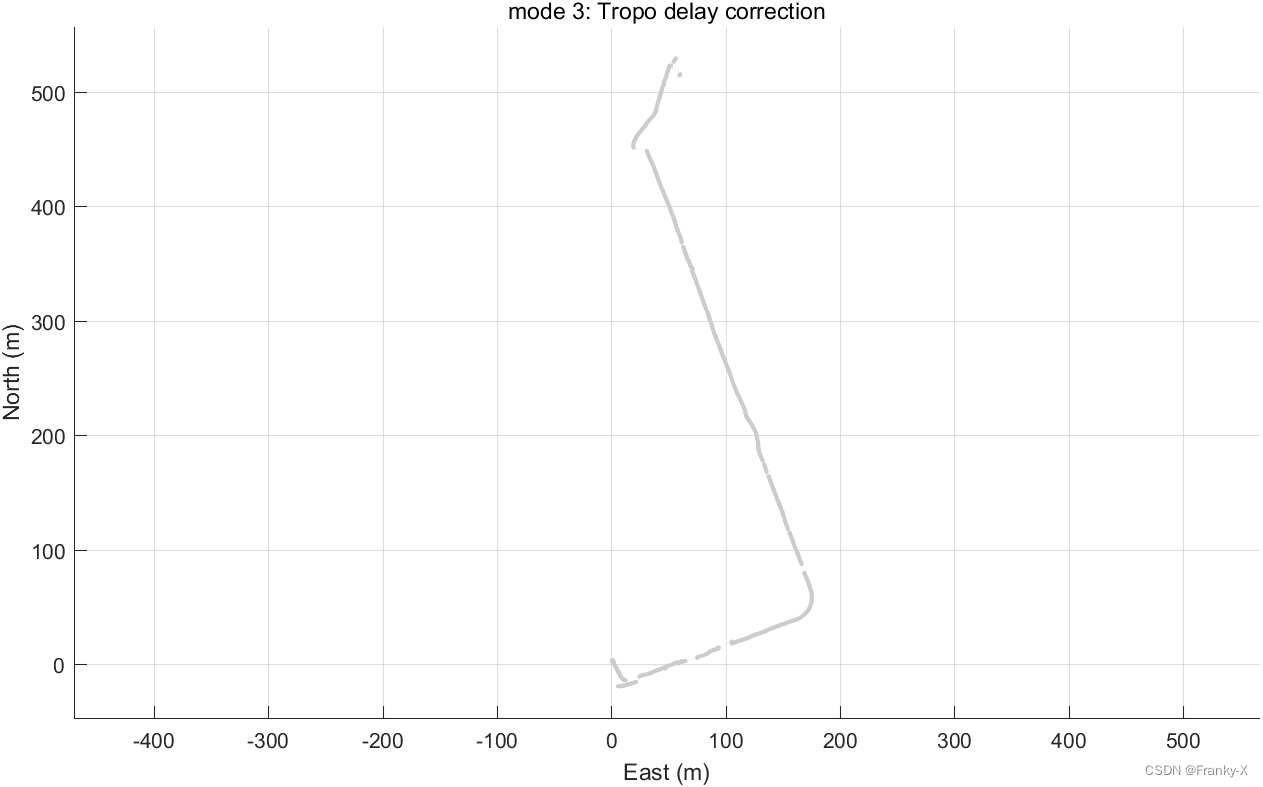
进一步，我们对BDS移动站的定位误差，NMEA格式文件导入RTKPLOT中，同时将参考真值的轨迹文件也导入RTKPLOT中进行比较。如图，BDS的移动站定位结果在水平方向上为10m左右，在垂直方向上的定位误差在20m左右，与SPP定位精度量级一致。

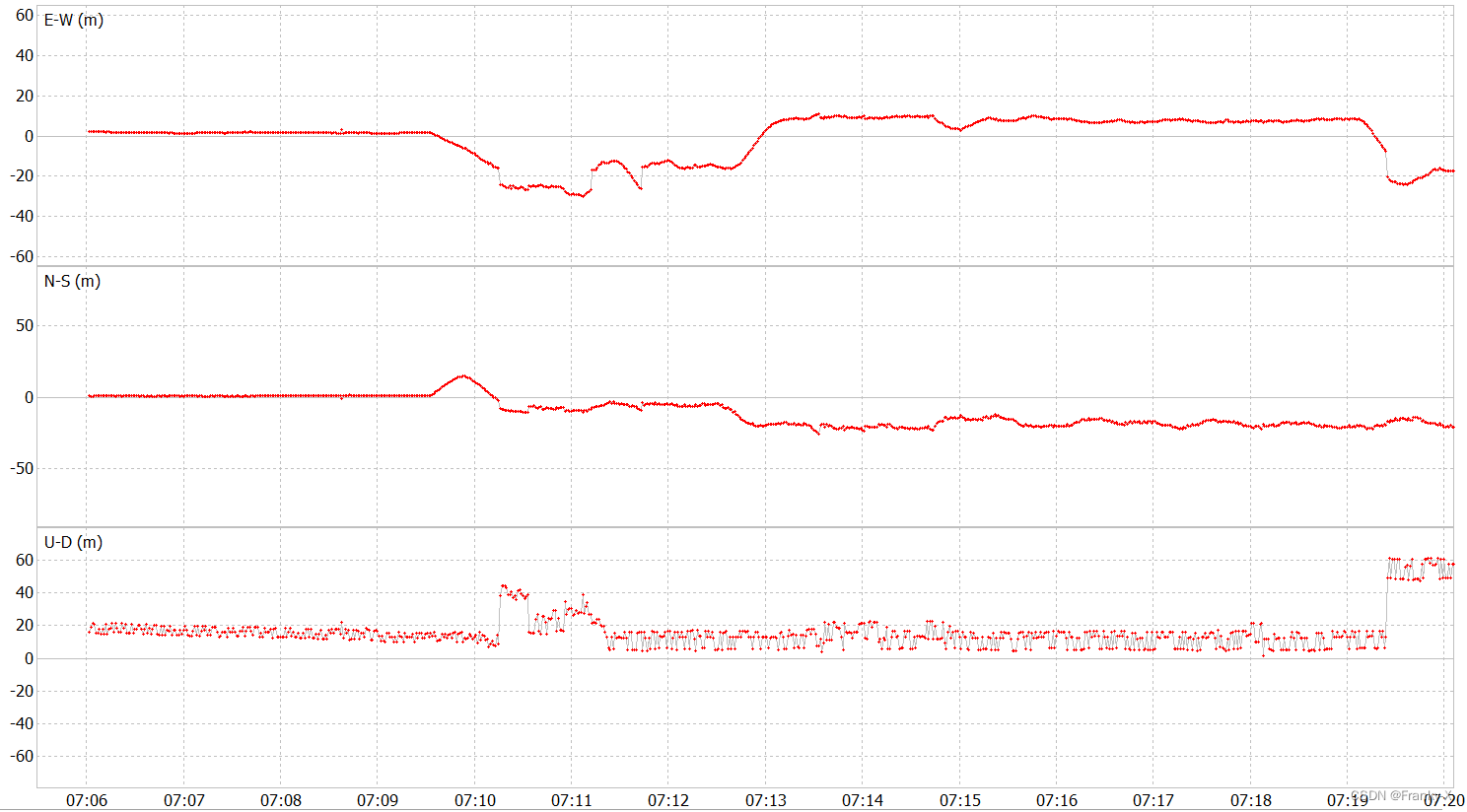
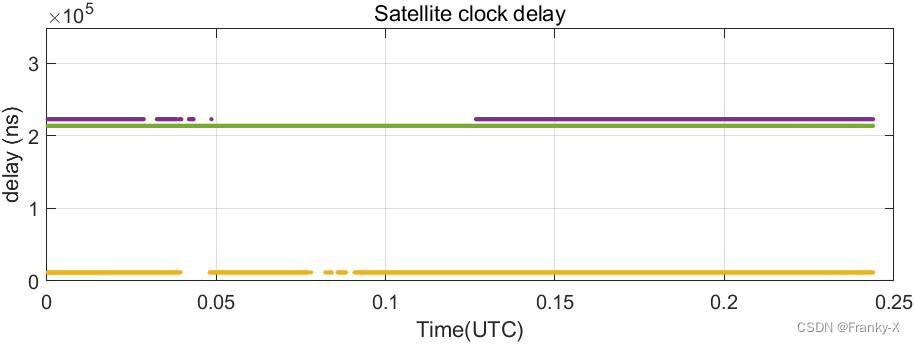
进而，我们分析了BDS的移动站可见性，如图所示，移动站的北斗卫星可见性相对较好，卫星数目较多，虽然北斗卫星的广播星历没有那么准确，但是可见卫星比GPS系统多，因此定位结果更加稳定。

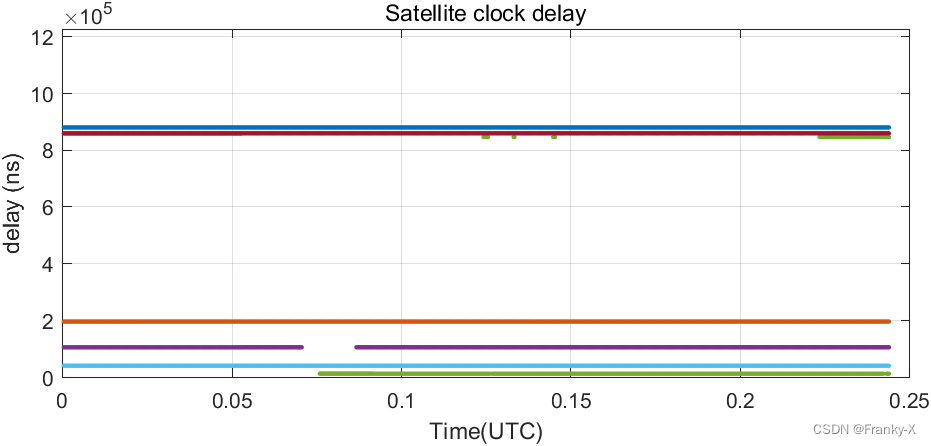
Conclusions

本报告用Matlab实现了SPP算法，支持RINEX 3.03格式，能进行GPS和BDS系统SPP定位。报告中先介绍了SPP算法的理论，包括RINEX文件格式、卫星位置与钟差解算以及最小二乘问题构建。接着，报告详细介绍了SPP算法的实现过程与工程技巧。最后，报告开展了SPP定位算法实验，分别使用GPS和BDS系统对固定站和移动站进行了定位，并对比其解算结果并分析了误差原因。本报告及其代码将开源于卫星社区，为卫星定位的学习者们提供参考。