每日一题蓝桥：幻方填空_719

1.题目

2.AC前所需的知识

这道需要用到数组全排列的知识以及用递归来完成数组的全排列

2.1简单理解一下全排列

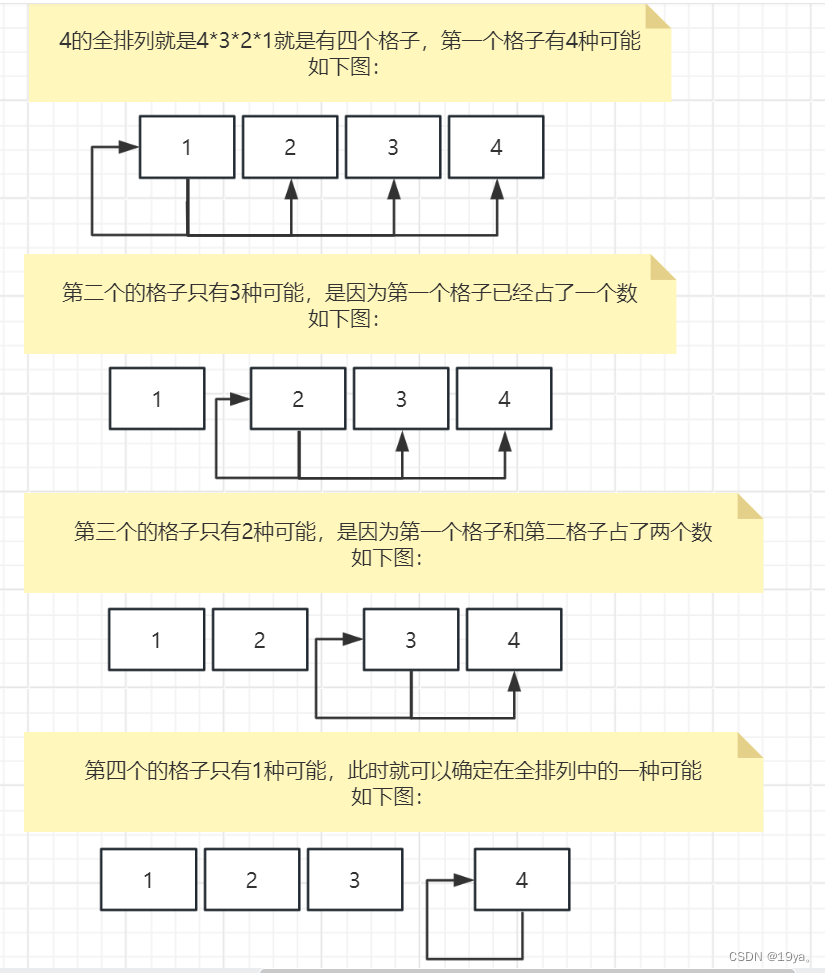
2.2用递归完成数组的全排列

2.2.1.给定一个长度为n的数组，可以通过递归实现全排列的过程，步骤如下：

1. 定义一个递归函数，接受当前数组、当前位置和数组长度作为参数；
2. 如果当前位置等于数组长度，表示已经完成了一种排列，可以输出结果；
3. 否则，从当前位置开始，依次与后面的元素进行交换，并递归调用函数，继续处理下一个位置；
4. 每次递归调用结束后，需要将交换的元素还原回原始状态，保证不影响其他排列的生成。
5. 在主函数中调用递归函数，初始时，将数组的起始位置和长度传入。

2.2.2. 以下是使用Java代码实现上述思路的例子：

public class Permutation {
    public static void main(String[] args) {
        int[] nums = {1, 2, 3, 4};
        permute(nums, 0, nums.length);
    }

    private static void permute(int[] nums, int start, int length) {
        if (start == length) {
            // 已经完成了一种排列，输出结果
            for (int num : nums) {
                System.out.print(num + " ");
            }
            System.out.println();
        } else {
            for (int i = start; i < length; i++) {
                swap(nums, start, i); // 将当前位置的元素与后面的元素逐个交换
                permute(nums, start + 1, length); // 继续处理下一个位置
                swap(nums, start, i); // 还原交换的元素
            }
        }
    }

    private static void swap(int[] nums, int i, int j) {
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }
}

以上代码会输出数组{1, 2, 3, 4}的全排列结果。你可以根据需要修改数组的内容和长度，并通过调用permute函数来获取全排列的结果。

2.3解疑惑

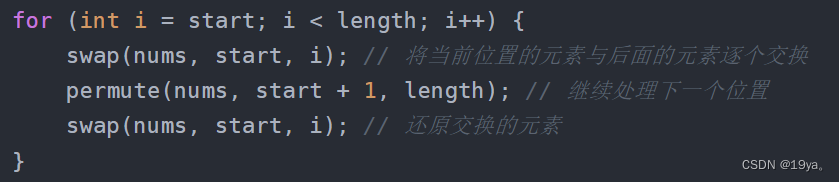
中的swap(nums, start, i)的作用或说是意义

3.题解

package 刷题记录;

public class 幻方填空_719 {
	public static void main(String[] args) {
		//幻方还缺失的数据
		int a[] = {2,3,4,5,6,7,8,10,12,14};
		f(a, 0, a.length);
	}
	static void f(int a[],int start,int end) {
		//1.递归结束条件
		if (start == end) {
			//符合要求输出*的值
			if (check(a)) {
				System.out.println(a[7]);
				return;
			}
		}
		//2.这是全排列的递归函数
		for (int k = start; k < end; k++) {
			//可以理解为：一次循环就遍历数组中[2,3,4,....,14]的一个值
			//start 相当于 源格子 ， k 相当于 要被替换的格子
			swap(a, start, k);
			//可以理解为：已确定一个格子的值，开始处理另一个格子了
			f(a, start + 1, end);
			//还原初始状态。可以理解为：前面借了，现在用完了，还回去。
			swap(a, start, k);
		}
	}
	//判断是否符合条件的函数
	static boolean check(int a[]) {
		//计算各行和
		int h1 = 16 + a[0] + a[1] + 13;
		int h2 = a[2] + a[3] + 11 + a[4];
		int h3 = 9 + a[5] + a[6] + a[7];
		int h4 = a[8] + 15 + a[9] + 1;
		//计算各列和
		int l1 = 16 + a[2] + 9 + a[8];
		int l2 = a[0] + a[3] + a[5] + 15;
		int l3 = a[1] + 11 + a[6] + a[9];
		int l4 = 13 + a[4] + a[7] + 1;
		//计算两条对角线
		int x1 = 16 + a[3] + a[6] + 1;
		int x2 = 13 + 11 + a[5] + a[8];
		if (h1==h2&&h2==h3&&h3==h4&&
			h4==l1&&l1==l2&&l2==l3&&l3==l4&&
			l4==x1&&x1==x2) {
			return true;
		}
		return false;
	}
	//置换数组位置的函数
	static void swap(int a[] , int i , int j) {
		int t = a[i] ;
		a[i] = a[j];
		a[j] = t ; 
	}
}

4.总结

这道题主要就是需要理解数组全排列的递归思想，理解了就可以轻松解决此题。

5.期望

这题可能有些复杂，我已尽力解释清楚。如果有任何错误或不清楚的地方，请随时指出。