助力工业生产“智造”,基于YOLOv8全系列模型【n/s/m/l/x】开发构建纺织生产场景下布匹瑕疵检测识别系统
纯粹的工业制造没有办法有长久的发展过程,转制造为全流程全场景的生产智造才是未来最具竞争力的生产场景,在前面的开发实践中我们已经涉足工业生产场景下进行了很多实地的项目开发,如:PCB电路板缺陷检测、焊接缺陷检测、螺母螺钉缺损检测等等,本文的主要目的就是想要基于最新的v8系列的模型来开发构建纺织生产场景下的布匹瑕疵检测识别系统。
布匹瑕疵检测在我们前面的文章中已经有了相关的实践,感兴趣的话可以自行移步阅读即可:
《布匹瑕疵检测实践大全,基于yolov5全系列模型[n/s/m/l/x]开发构建布匹瑕疵检测模型,对比分析各个模型性能差异》《集成注意力机制基于YOLOv5开发构建布匹瑕疵检测识别系统》
?本文主要是选择最新的YOLOv8来开发实现检测模型,我们开发了五款不同参数量级的模型用于整体对比分析,首先看下实例效果:
简单看下实例数据情况:


训练数据配置文件如下所示:
# Dataset
path: ./dataset
train:
- /data/dataset/images/train
val:
- /data/dataset/images/test
test:
- /data/dataset/images/test
# Classes
names:
0: chongzhan
1: cuohua
2: fengtou
3: fengtouyin
4: huamao
5: laban
6: louyin
7: podong
8: qita
9: secha
10: shuiyin
11: wangzhe
12: zhanwu
13: zhezi
14: zhici如果对YOLOv8开发构建自己的目标检测项目有疑问的可以看下面的文章,如下所示:
《基于YOLOv8开发构建目标检测模型超详细教程【以焊缝质量检测数据场景为例】》
非常详细的开发实践教程。本文这里就不再展开了,因为从YOLOv8开始变成了一个安装包的形式,整体跟v5和v7的使用差异还是比较大的。
YOLOv8核心特性和改动如下:
1、提供了一个全新的SOTA模型(state-of-the-art model),包括 P5 640 和 P6 1280 分辨率的目标检测网络和基于YOLACT的实例分割模型。和 YOLOv5 一样,基于缩放系数也提供了 N/S/M/L/X 尺度的不同大小模型,用于满足不同场景需求
2、骨干网络和 Neck 部分可能参考了 YOLOv7 ELAN 设计思想,将 YOLOv5 的 C3 结构换成了梯度流更丰富的 C2f 结构,并对不同尺度模型调整了不同的通道数,属于对模型结构精心微调,不再是一套参数应用所有模型,大幅提升了模型性能。
3、Head 部分相比 YOLOv5 改动较大,换成了目前主流的解耦头结构,将分类和检测头分离,同时也从Anchor-Based 换成了 Anchor-Free
4、Loss 计算方面采用了TaskAlignedAssigner正样本分配策略,并引入了Distribution Focal Loss
5、训练的数据增强部分引入了 YOLOX 中的最后 10 epoch 关闭 Mosiac 增强的操作,可以有效地提升精度
官方项目地址在这里,如下所示:


目前已经收获超过1.7w的star量了。官方提供的预训练模型如下所示:
| Model | size (pixels) | mAPval 50-95 | Speed CPU ONNX (ms) | Speed A100 TensorRT (ms) | params (M) | FLOPs (B) |
|---|---|---|---|---|---|---|
| YOLOv8n | 640 | 37.3 | 80.4 | 0.99 | 3.2 | 8.7 |
| YOLOv8s | 640 | 44.9 | 128.4 | 1.20 | 11.2 | 28.6 |
| YOLOv8m | 640 | 50.2 | 234.7 | 1.83 | 25.9 | 78.9 |
| YOLOv8l | 640 | 52.9 | 375.2 | 2.39 | 43.7 | 165.2 |
| YOLOv8x | 640 | 53.9 | 479.1 | 3.53 | 68.2 | 257.8 |
另外一套预训练模型如下:
| Model | size (pixels) | mAPval 50-95 | Speed CPU ONNX (ms) | Speed A100 TensorRT (ms) | params (M) | FLOPs (B) |
|---|---|---|---|---|---|---|
| YOLOv8n | 640 | 18.4 | 142.4 | 1.21 | 3.5 | 10.5 |
| YOLOv8s | 640 | 27.7 | 183.1 | 1.40 | 11.4 | 29.7 |
| YOLOv8m | 640 | 33.6 | 408.5 | 2.26 | 26.2 | 80.6 |
| YOLOv8l | 640 | 34.9 | 596.9 | 2.43 | 44.1 | 167.4 |
| YOLOv8x | 640 | 36.3 | 860.6 | 3.56 | 68.7 | 260.6 |
是基于Open Image V7数据集构建的,可以根据自己的需求进行选择使用即可。
YOLOv8的定位不仅仅是目标检测,而是性能强大全面的工具库,故而在任务类型上同时支持:姿态估计、检测、分类、分割、跟踪多种类型,可以根据自己的需要进行选择使用,这里就不再详细展开了。
简单的实例实现如下所示:
from ultralytics import YOLO
# yolov8n
model = YOLO('yolov8n.yaml').load('yolov8n.pt') # build from YAML and transfer weights
model.train(data='data/self.yaml', epochs=100, imgsz=640)
# yolov8s
model = YOLO('yolov8s.yaml').load('yolov8s.pt') # build from YAML and transfer weights
model.train(data='data/self.yaml', epochs=100, imgsz=640)
# yolov8m
model = YOLO('yolov8m.yaml').load('yolov8m.pt') # build from YAML and transfer weights
model.train(data='data/self.yaml', epochs=100, imgsz=640)
# yolov8l
model = YOLO('yolov8l.yaml').load('yolov8l.pt') # build from YAML and transfer weights
model.train(data='data/self.yaml', epochs=100, imgsz=640)
# yolov8x
model = YOLO('yolov8x.yaml').load('yolov8x.pt') # build from YAML and transfer weights
model.train(data='data/self.yaml', epochs=100, imgsz=640)这里我们依次选择n、s、m、l和x五款不同参数量级的模型来进行开发。
这里给出yolov8的模型文件如下:
# Parameters
nc: 15 # number of classes
scales: # model compound scaling constants, i.e. 'model=yolov8n.yaml' will call yolov8.yaml with scale 'n'
# [depth, width, max_channels]
n: [0.33, 0.25, 1024] # YOLOv8n summary: 225 layers, 3157200 parameters, 3157184 gradients, 8.9 GFLOPs
s: [0.33, 0.50, 1024] # YOLOv8s summary: 225 layers, 11166560 parameters, 11166544 gradients, 28.8 GFLOPs
m: [0.67, 0.75, 768] # YOLOv8m summary: 295 layers, 25902640 parameters, 25902624 gradients, 79.3 GFLOPs
l: [1.00, 1.00, 512] # YOLOv8l summary: 365 layers, 43691520 parameters, 43691504 gradients, 165.7 GFLOPs
x: [1.00, 1.25, 512] # YOLOv8x summary: 365 layers, 68229648 parameters, 68229632 gradients, 258.5 GFLOPs
# YOLOv8.0n backbone
backbone:
# [from, repeats, module, args]
- [-1, 1, Conv, [64, 3, 2]] # 0-P1/2
- [-1, 1, Conv, [128, 3, 2]] # 1-P2/4
- [-1, 3, C2f, [128, True]]
- [-1, 1, Conv, [256, 3, 2]] # 3-P3/8
- [-1, 6, C2f, [256, True]]
- [-1, 1, Conv, [512, 3, 2]] # 5-P4/16
- [-1, 6, C2f, [512, True]]
- [-1, 1, Conv, [1024, 3, 2]] # 7-P5/32
- [-1, 3, C2f, [1024, True]]
- [-1, 1, SPPF, [1024, 5]] # 9
# YOLOv8.0n head
head:
- [-1, 1, nn.Upsample, [None, 2, 'nearest']]
- [[-1, 6], 1, Concat, [1]] # cat backbone P4
- [-1, 3, C2f, [512]] # 12
- [-1, 1, nn.Upsample, [None, 2, 'nearest']]
- [[-1, 4], 1, Concat, [1]] # cat backbone P3
- [-1, 3, C2f, [256]] # 15 (P3/8-small)
- [-1, 1, Conv, [256, 3, 2]]
- [[-1, 12], 1, Concat, [1]] # cat head P4
- [-1, 3, C2f, [512]] # 18 (P4/16-medium)
- [-1, 1, Conv, [512, 3, 2]]
- [[-1, 9], 1, Concat, [1]] # cat head P5
- [-1, 3, C2f, [1024]] # 21 (P5/32-large)
- [[15, 18, 21], 1, Detect, [nc]] # Detect(P3, P4, P5)囊括了五款不同参数量级的模型。在训练结算保持相同的参数设置,等待训练完成后我们横向对比可视化来整体对比分析。
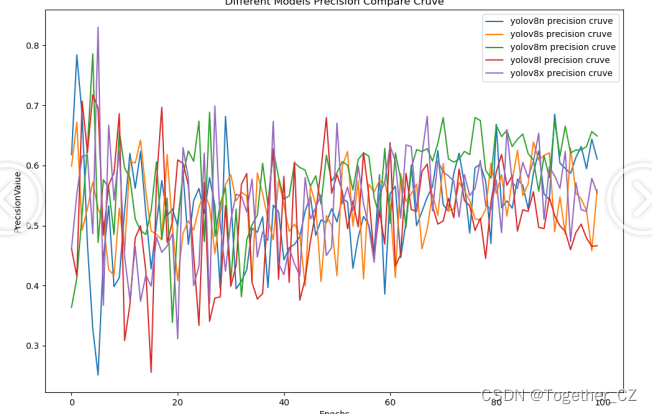
【Precision曲线】
精确率曲线(Precision-Recall Curve)是一种用于评估二分类模型在不同阈值下的精确率性能的可视化工具。它通过绘制不同阈值下的精确率和召回率之间的关系图来帮助我们了解模型在不同阈值下的表现。
精确率(Precision)是指被正确预测为正例的样本数占所有预测为正例的样本数的比例。召回率(Recall)是指被正确预测为正例的样本数占所有实际为正例的样本数的比例。
绘制精确率曲线的步骤如下:
使用不同的阈值将预测概率转换为二进制类别标签。通常,当预测概率大于阈值时,样本被分类为正例,否则分类为负例。
对于每个阈值,计算相应的精确率和召回率。
将每个阈值下的精确率和召回率绘制在同一个图表上,形成精确率曲线。
根据精确率曲线的形状和变化趋势,可以选择适当的阈值以达到所需的性能要求。
通过观察精确率曲线,我们可以根据需求确定最佳的阈值,以平衡精确率和召回率。较高的精确率意味着较少的误报,而较高的召回率则表示较少的漏报。根据具体的业务需求和成本权衡,可以在曲线上选择合适的操作点或阈值。
精确率曲线通常与召回率曲线(Recall Curve)一起使用,以提供更全面的分类器性能分析,并帮助评估和比较不同模型的性能。
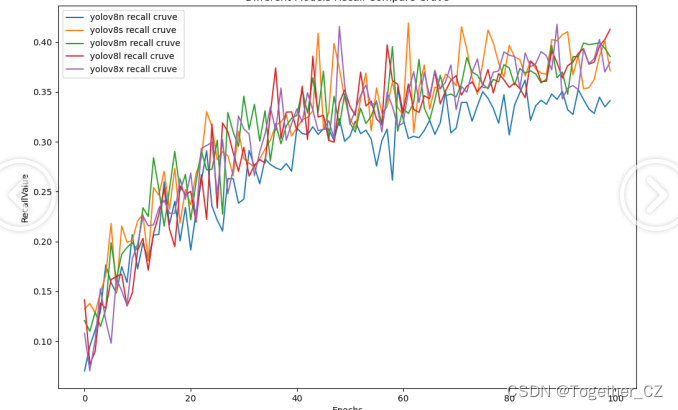
【Recall曲线】
召回率曲线(Recall Curve)是一种用于评估二分类模型在不同阈值下的召回率性能的可视化工具。它通过绘制不同阈值下的召回率和对应的精确率之间的关系图来帮助我们了解模型在不同阈值下的表现。
召回率(Recall)是指被正确预测为正例的样本数占所有实际为正例的样本数的比例。召回率也被称为灵敏度(Sensitivity)或真正例率(True Positive Rate)。
绘制召回率曲线的步骤如下:
使用不同的阈值将预测概率转换为二进制类别标签。通常,当预测概率大于阈值时,样本被分类为正例,否则分类为负例。
对于每个阈值,计算相应的召回率和对应的精确率。
将每个阈值下的召回率和精确率绘制在同一个图表上,形成召回率曲线。
根据召回率曲线的形状和变化趋势,可以选择适当的阈值以达到所需的性能要求。
通过观察召回率曲线,我们可以根据需求确定最佳的阈值,以平衡召回率和精确率。较高的召回率表示较少的漏报,而较高的精确率意味着较少的误报。根据具体的业务需求和成本权衡,可以在曲线上选择合适的操作点或阈值。
召回率曲线通常与精确率曲线(Precision Curve)一起使用,以提供更全面的分类器性能分析,并帮助评估和比较不同模型的性能。
【F1值曲线】
F1值曲线是一种用于评估二分类模型在不同阈值下的性能的可视化工具。它通过绘制不同阈值下的精确率(Precision)、召回率(Recall)和F1分数的关系图来帮助我们理解模型的整体性能。
F1分数是精确率和召回率的调和平均值,它综合考虑了两者的性能指标。F1值曲线可以帮助我们确定在不同精确率和召回率之间找到一个平衡点,以选择最佳的阈值。
绘制F1值曲线的步骤如下:
使用不同的阈值将预测概率转换为二进制类别标签。通常,当预测概率大于阈值时,样本被分类为正例,否则分类为负例。
对于每个阈值,计算相应的精确率、召回率和F1分数。
将每个阈值下的精确率、召回率和F1分数绘制在同一个图表上,形成F1值曲线。
根据F1值曲线的形状和变化趋势,可以选择适当的阈值以达到所需的性能要求。
F1值曲线通常与接收者操作特征曲线(ROC曲线)一起使用,以帮助评估和比较不同模型的性能。它们提供了更全面的分类器性能分析,可以根据具体应用场景来选择合适的模型和阈值设置。

综合对比来看:不同参数量级的模型在性能上没有拉开明显的差距,相比之下,n系列的模型效果最低,m系列的模型更为优异,最终我们选择了m系列的模型作为线上的推理模型了。
接下来我们详细看下m系列模型的结果:
【Batch实例】

【训练可视化】

感兴趣的话也都可以自行动手实践下!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 如何让亚马逊,速卖通,美客多店铺排名和流量稳定爬升
- c++异常
- 圣诞节到了,用js给喜欢的人写一颗圣诞树吧
- 考研护眼台灯哪种质量好?口碑好的五款台灯分享
- AI真正的Killer App 仍然缺席
- RK3568平台(网络篇) 有线网络基本概念及测试手法
- 【JAVA】Java并发编程中的锁升级机制
- HarmonyOS4.0开发该怎么系统学习,适合哪些人?
- 解锁高效工作!5款优秀工时管理软件推荐
- 软件测试-----黑盒测试与白盒测试