【Pytorch】学习记录分享3——PyTorch 自动微分与线性回归
发布时间:2023年12月17日
【【Pytorch】学习记录分享3——PyTorch 自动微分与线性回归
小结:只需要将前向传播设置好,调用反向传播接口,即可实现反向传播的链式求导
1. autograd 包,自动微分
自动微分是机器学习工具包必备的工具,它可以自动计算整个计算图的微分。
PyTorch内建了一个叫做torch.autograd的自动微分引擎,该引擎支持的数据类型为:浮点数Tensor类型 ( half, float, double and bfloat16) 和复数Tensor 类型(cfloat, cdouble)
PyTorch中与自动微分相关的常用的Tensor属性和函数:
属性requires_grad:
默认值为False,表明该Tensor不会被自动微分引擎计算微分。设置为True,表明让自动微分引擎计算该Tensor的微分
属性grad:存储自动微分的计算结果,即调用backward()方法后的计算结果
方法backward(): 计算微分,一般不带参数,等效于:backward(torch.tensor(1.0))。若backward()方法在DAG的root上调用,它会依据链式法则自动计算DAG所有枝叶上的微分。
方法no_grad():禁用自动微分上下文管理, 一般用于模型评估或推理计算这些不需要执行自动微分计算的地方,以减少内存和算力的消耗。另外禁止在模型参数上自动计算微分,即不允许更新该参数,即所谓的冻结参数(frozen parameters)。
zero_grad()方法:PyTorch的微分是自动积累的,需要用zero_grad()方法手动清零
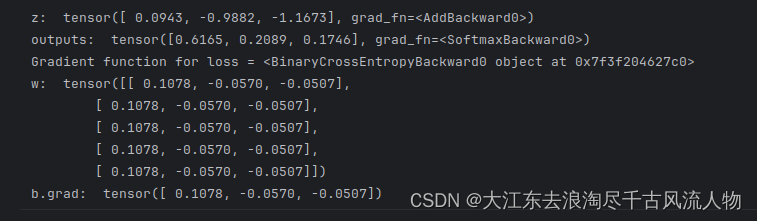
# 模型:z = x@w + b;激活函数:Softmax
x = torch.ones(5) # 输入张量,shape=(5,)
labels = torch.zeros(3) # 标签值,shape=(3,)
w = torch.randn(5,3,requires_grad=True) # 模型参数,需要计算微分, shape=(5,3)
b = torch.randn(3, requires_grad=True) # 模型参数,需要计算微分, shape=(3,)
z = x@w + b # 模型前向计算
outputs = torch.nn.functional.softmax(z) # 激活函数
print("z: ",z)
print("outputs: ",outputs)
loss = torch.nn.functional.binary_cross_entropy(outputs, labels)
# 查看loss函数的微分计算函数
print('Gradient function for loss =', loss.grad_fn)
# 调用loss函数的backward()方法计算模型参数的微分
loss.backward()
# 查看模型参数的微分值
print("w: ",w.grad)
print("b.grad: ",b.grad)
小姐:
| 方法 | 描述 |
|---|---|
| .requires_grad 设置为True | 会开始跟踪针对 tensor 的所有操作 |
| .backward() | 张量的梯度将累积到 .grad 属性 |
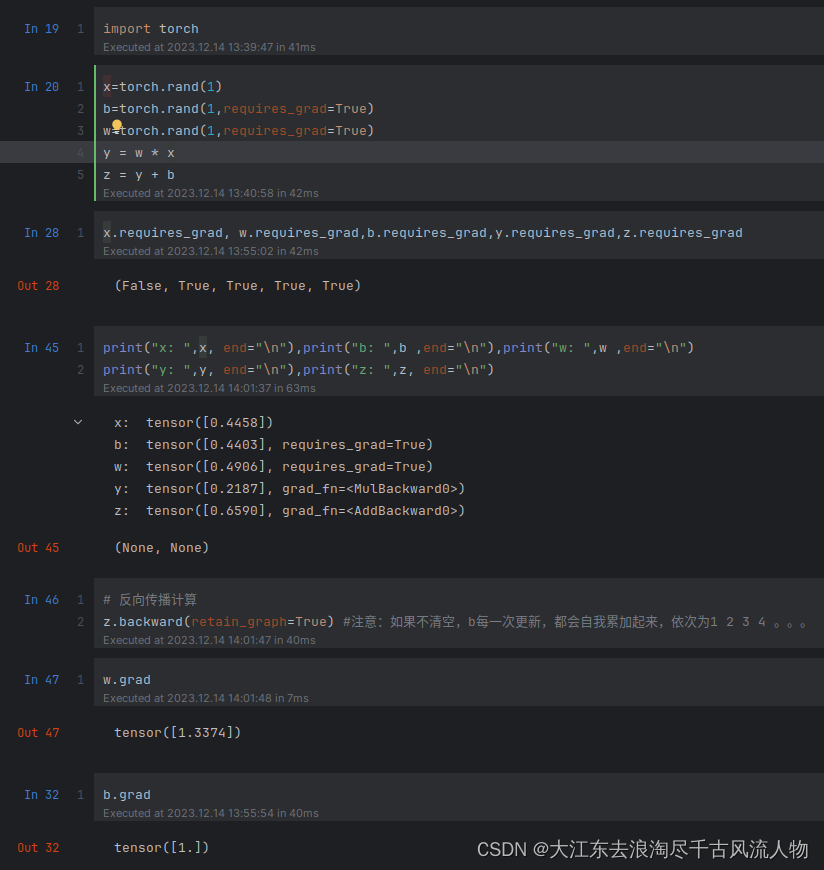
import torch
x=torch.rand(1)
b=torch.rand(1,requires_grad=True)
w=torch.rand(1,requires_grad=True)
y = w * x
z = y + b
x.requires_grad, w.requires_grad,b.requires_grad,y.requires_grad,z.requires_grad
print("x: ",x, end="\n"),print("b: ",b ,end="\n"),print("w: ",w ,end="\n")
print("y: ",y, end="\n"),print("z: ",z, end="\n")
# 反向传播计算
z.backward(retain_graph=True) #注意:如果不清空,b每一次更新,都会自我累加起来,依次为1 2 3 4 。。。
w.grad
b.grad
运行结果:
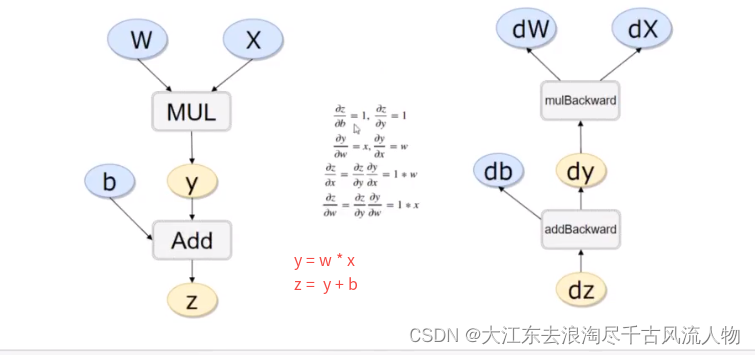
反向传播求导原理:
2. 线性模型回归演示

import torch
import torch.nn as nn
## 线性回归模型: 本质上就是一个不加 激活函数的 全连接层
class LinearRegressionModel(nn.Module):
def __init__(self, input_size, output_size):
super(LinearRegressionModel, self).__init__()
self.linear = nn.Linear(input_size, output_size)
def forward(self, x):
out = self.linear(x)
return out
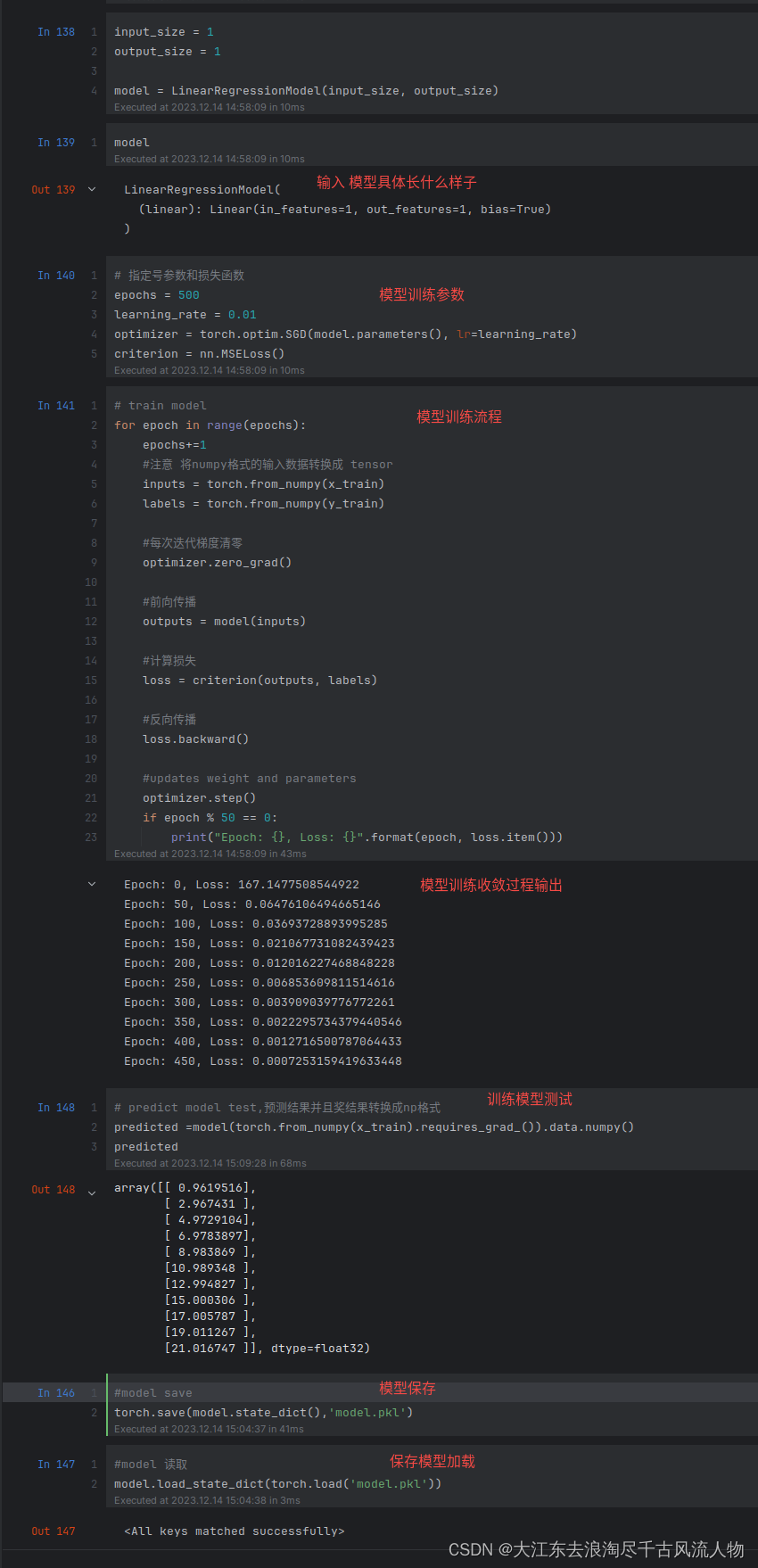
input_size = 1
output_size = 1
model = LinearRegressionModel(input_size, output_size)
model
# 指定号参数和损失函数
epochs = 500
learning_rate = 0.01
optimizer = torch.optim.SGD(model.parameters(), lr=learning_rate)
criterion = nn.MSELoss()
# train model
for epoch in range(epochs):
epochs+=1
#注意 将numpy格式的输入数据转换成 tensor
inputs = torch.from_numpy(x_train)
labels = torch.from_numpy(y_train)
#每次迭代梯度清零
optimizer.zero_grad()
#前向传播
outputs = model(inputs)
#计算损失
loss = criterion(outputs, labels)
#反向传播
loss.backward()
#updates weight and parameters
optimizer.step()
if epoch % 50 == 0:
print("Epoch: {}, Loss: {}".format(epoch, loss.item()))
# predict model test,预测结果并且奖结果转换成np格式
predicted =model(torch.from_numpy(x_train).requires_grad_()).data.numpy()
predicted
#model save
torch.save(model.state_dict(),'model.pkl')
#model 读取
model.load_state_dict(torch.load('model.pkl'))
3. GPU进行模型训练
只需要 将模型和数据传入到“cuda”中运行即可,详细实现见截图
import torch
import torch.nn as nn
import numpy as np
# #构建一个回归方程 y = 2*x+1
#构建输如数据,将输入numpy格式转成tensor格式
x_values = [i for i in range(11)]
x_train = np.array(x_values,dtype=np.float32)
x_train = x_train.reshape(-1,1)
y_values = [2*i + 1 for i in x_values]
y_train = np.array(y_values, dtype=np.float32)
y_train = y_train.reshape(-1,1)
## 线性回归模型: 本质上就是一个不加 激活函数的 全连接层
class LinearRegressionModel(nn.Module):
def __init__(self, input_size, output_size):
super(LinearRegressionModel, self).__init__()
self.linear = nn.Linear(input_size, output_size)
def forward(self, x):
out = self.linear(x)
return out
input_size = 1
output_size = 1
model = LinearRegressionModel(input_size, output_size)
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
model.to(device)
# 指定号参数和损失函数
epochs = 500
learning_rate = 0.01
optimizer = torch.optim.SGD(model.parameters(), lr=learning_rate)
criterion = nn.MSELoss()
# train model
for epoch in range(epochs):
epochs+=1
#注意 将numpy格式的输入数据转换成 tensor
inputs = torch.from_numpy(x_train)
labels = torch.from_numpy(y_train)
#每次迭代梯度清零
optimizer.zero_grad()
#前向传播
outputs = model(inputs)
#计算损失
loss = criterion(outputs, labels)
#反向传播
loss.backward()
#updates weight and parameters
optimizer.step()
if epoch % 50 == 0:
print("Epoch: {}, Loss: {}".format(epoch, loss.item()))
# predict model test,预测结果并且奖结果转换成np格式
predicted = model(torch.from_numpy(x_train).requires_grad_()).data.numpy()
predicted
#model save
torch.save(model.state_dict(),'model.pkl')

文章来源:https://blog.csdn.net/Darlingqiang/article/details/134990622
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- NPDP产品经理必备证书!主要考什么?怎么考?
- 电脑弹窗‘找不到msvcp120dll,无法继续执行代码’要怎么解决?快速修复msvcp120dll
- 机器视觉【1】相机的成像(畸变)模型
- 大哈的变换迷宫的题解
- Kerberos安装教程与命令详解(超详细)
- echarts地图的常见用法:基本使用、区域颜色分级、水波动画、区域轮播、给地图添加背景图片和图标、3d地图、飞线图
- lnmp搭建{nfs,负载均衡}
- 混合背包问题
- 超详细的企业单位B级数据机房施工方案
- Netty通信中的粘包半包问题(四)