Codeforces Round 920 (Div. 3) F题 根号分治，后缀和，后缀和的后缀和

Problem - F - Codeforces?

我看的这位UP的视频讲解 ：

Codeforces Round 920 (Div. 3) F题 根号分治 详解_哔哩哔哩_bilibili

?

目录

题意：

思路：

后缀和的后缀和:

后缀和的后缀和的中间段如何求：

————

根号分治:

核心代码：

---

?

题意：

给你个数组，求这个和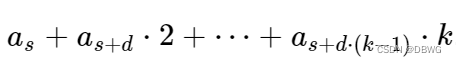

s是起始下标，d是间隔gap，k代表第几个数乘以几。

思路：

暴力过不了。需要后缀和预处理。

后缀和的后缀和:

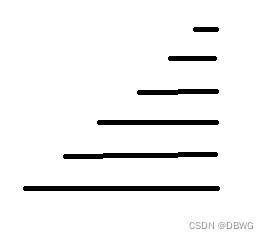
如图，这是几组后缀和，你会发现他们加起来后，第几个位置就是几倍的那个数。

看不懂看这个理解一下：

（黑线就是这串后缀数）

（比如我们把他们全部加起来，正好第六个数就加了6次，就是乘了k)

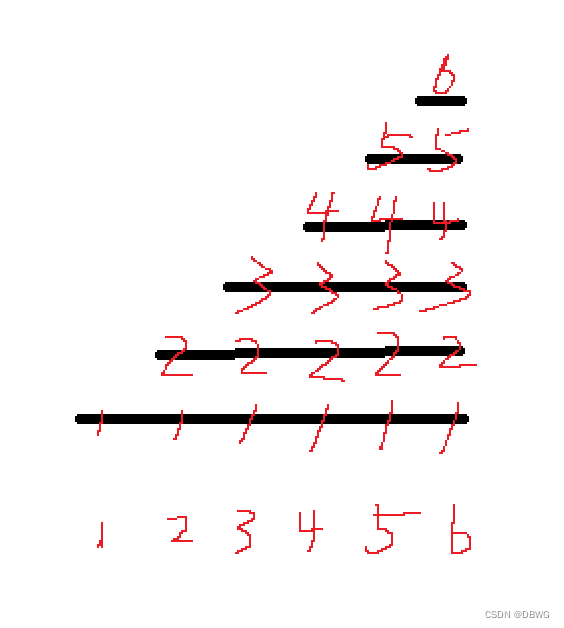
后缀和的后缀和的中间段如何求：

然后就是中间段的这个如何求呢？?

不是直接用后缀和的后缀和去减后缀和的后缀和，这样减完是“平行”的，后面的没有被消掉：

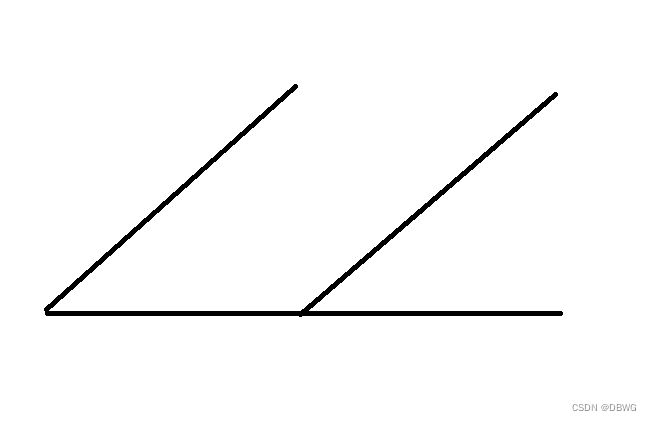（斜线就代表后缀和的后缀和）

比如下图我们用a的减去b的，只减了“X”部分，而“O”部分没有被减去：

?

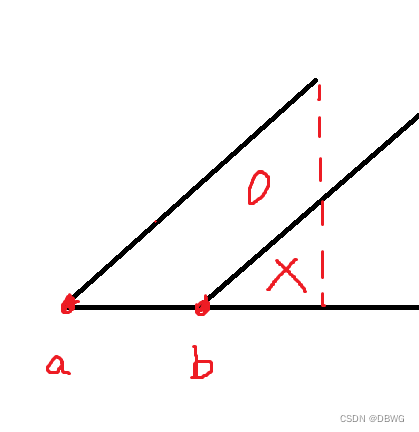
不过显而易见，需要减得“O”部分是平行的，即减去他们正常后缀和的某个倍数即可。

我们算b需要减几倍即可：

这里中间段其实是a到b-1，b-1就是第k个数了。那么下一个数的后缀和的后缀和是k+1倍。不过我们减去?1被了，所以还需要减去k倍。

即后面的数都要减k倍。

————

根号分治:

单纯后缀和也过不了，因为当间隔足够大时（这里是根号n，即sqrt(n)），暴力就足够快啦，反而在数组中记录后缀和会浪费空间。（比如间隔n个，那就一个数放一个位置；间隔n-1个也就第一个数不是自己，这就没必要用后缀和啦，暴力就可以）

所以我们求后缀和只求到间隔为sqrt(n)就好啦。

核心代码：

#define ll long long
const ll inf = 1e9;
void solve()
{
	int n, q; cin >> n >> q;
	vector<ll>arr(n + 1);
	for (int i = 1; i <= n; i++)//从1开始。。
		cin >> arr[i];
	//
	//隔d的后缀和 // 把这些后缀和加起来 -> 逐项升数目的后缀和
	int nsqrt = sqrt(n);
	vector<vector<ll>>tarr(nsqrt + 1,vector<ll>(n + 1)), tkarr(nsqrt + 1, vector<ll>(n+1));
	for (int i = 1; i <= nsqrt; i++)
	{
		for (int j = n; j >= 1; j --)
		{
			tarr[i][j] = arr[j]+(j + i > n ? 0:tarr[i][j+i]);
		}
	}
	for (int i = 1; i <= nsqrt; i++)
	{
		for (int j = n; j >= 1; j --)
		{
			tkarr[i][j] = tarr[i][j] + (j + i > n ? 0 : tkarr[i][j + i]);
		}
	}

	for (int i = 1; i <= q; i++)
	{
		int s, d, k;
		cin >> s >> d >> k;
	
		if (d<=nsqrt)
		{
			cout << tkarr[d][s] - (s+d*k>n?0:tkarr[d][s+d*k] + tarr[d][s + d*k]*k)  << " ";
		}
		else
		{
			//暴力
			ll sum = 0;
			for (ll j = 1; j <= k && s <= n; j++)
			{
				sum += arr[s] * j;
				s += d;
			}
			cout << sum << " ";
		}
	}