第八章 假设检验(重难点)
发布时间:2023年12月27日
1.原假设H0和备择假设H1,深刻记住概念:


?注意:
H0,是想反对的假设,永远放等号的一方。比如大于,大于等于,小于等于三个符号。
H1,是想支持的一方,总有不等号,大于,小于的符号。
2.假设检验的两类错误:

3.检验假设的重要知识点:
一、下面是一个总体的情况?
前提(都假设总体服从正态分布,或者不服从时n大于等于30情况下近似服从正态分布)
分为三种情况:
1.总体均值的检验根据总体方差未已知和大小样本,分为三种情况(使用Z,Z和t检验)
2.总体比例的检验(z检验)
3.总体方差的检验(卡方检验)
二、下面是两个总体的情况
前提(都假设总体服从正态分布,或者不服从时n大于等于30情况下近似服从正态分布)
分为四种情况:
1.两个总体均值之差的检验(根据总体方差和大小样本变化分三种情况,用Z或t统计量)
2.匹配样本的t检验(一个总体经过前后变化得到两份数据)
3.两个总体比例之差的检验(Z检验)
4.两个总体方差比的检验(F检验)
具体展开如下



?
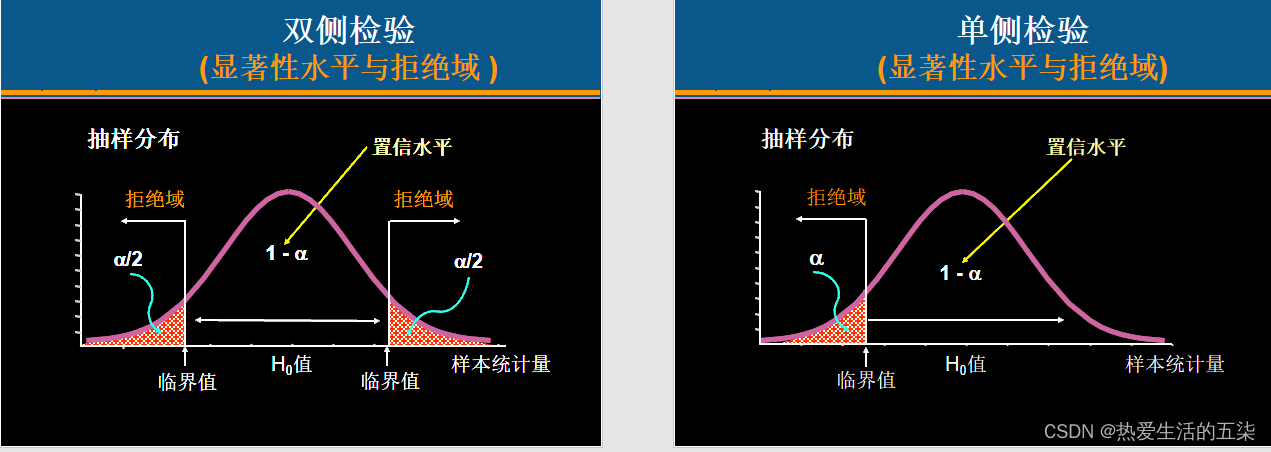
一、下面是一个总体的情况?
前提(都假设总体服从正态分布,或者不服从时n大于等于30情况下近似服从正态分布)
分为三种情况:
1.总体均值的检验根据总体方差未已知和大小样本,分为三种情况(使用Z,Z和t检验)
2.总体比例的检验(z检验)
3.总体方差的检验(卡方检验)
?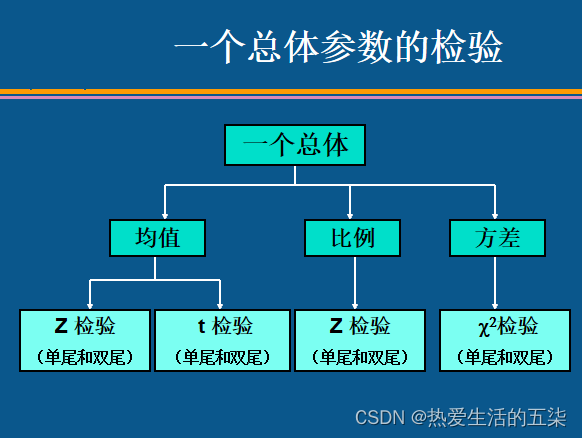
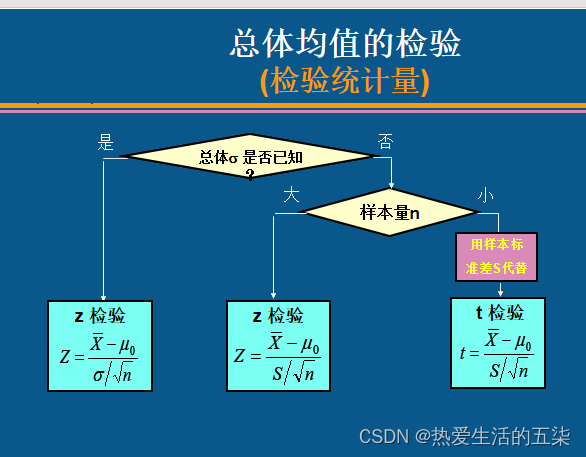
?1.下面是一个总体时总体均值的的检验
?
?

2.一个总体比例的检验:

3.一个总体方差的检验:
 二、下面是两个总体的情况
二、下面是两个总体的情况
前提(都假设总体服从正态分布,或者不服从时n大于等于30情况下近似服从正态分布)
分为四种情况:
1.两个总体均值之差的检验(根据总体方差和大小样本变化分三种情况,用Z或t统计量)
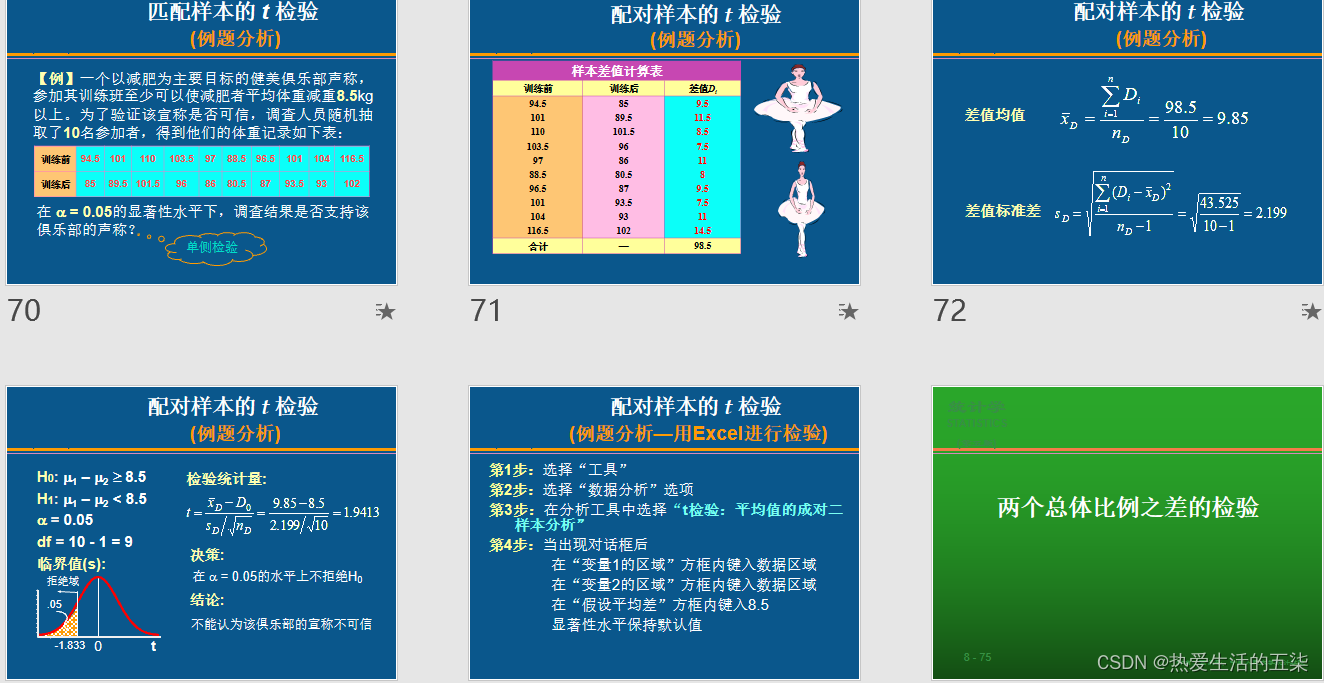
2.匹配样本的t检验(一个总体经过前后变化得到两份数据)
3.两个总体比例之差的检验(Z检验)
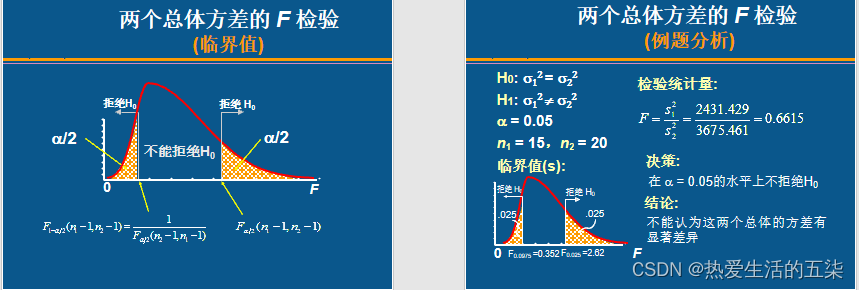
4.两个总体方差比的检验(F检验)
?

?
 ?
?
?
?
文章来源:https://blog.csdn.net/weixin_44162814/article/details/135236782
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 格密码基础:NTRU格
- 预测!全年乘用车交付或超2100万辆,比亚迪、华为「忙促销」
- 【IEEE会议征稿】2024年第九届智能计算与信号处理国际学术会议(ICSP 2024)
- 大哥你做科研 做它有啥用啊|2024元旦快乐
- SpringBoot+Vue & 跨域 & 页面布局
- 引爆年轻消费市场?用虚拟人结合动捕设备,拓宽营销边界
- mybtis动态SQL注解 脚本动态SQL\方法中构建SQL\SQL语句构造器
- Python3.10.6安装
- H5C3练习心得2024.01.05(鼠标移入旋转动画)--filter,::after,z-index
- MidTool的Midjourney:将AI创作的艺术转化为NFT