数学建模算法0基础学习第一天-层次分析法

目录

一、什么是层次分析法

1.定义部分

2.解释部分

二、学习层次分析法

1.学习准备

2.学习路线

1.问题的提出

2.解决问题

---

一、什么是层次分析法

1.定义部分

层次分析法根据问题的性质和要达到的总目标，将问题分解为不同的组成因素，并按照因素间的相互关联影响以及隶属关系将因素按不同层次聚集组合，形成一个多层次的分析结构模型，从而最终使问题归结为最低层(供决策的方案、措施等)相对于最高层(总目标)的相对重要权值的确定或相对优劣次序的排定

2.解释部分

对于各种指标进行加权的赋值对比统计，进而得出相应的决策。

二、学习层次分析法

1.学习准备

我将在后面逐一解释

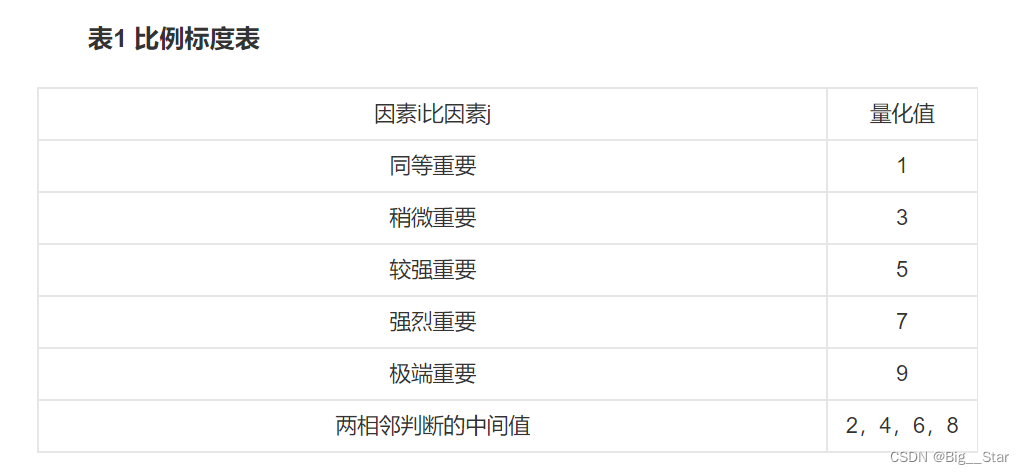
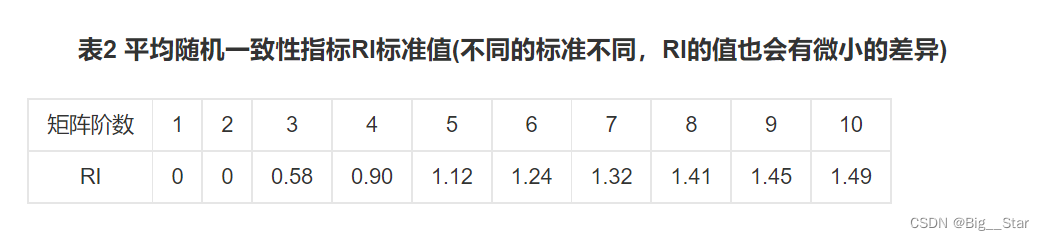
权重的计算方法

1.算术平均法求权重

假设有三个样本数据：a=3，b=5，c=7。通过算术平均法求出这三个样本数据的权重。

首先计算平均值：(3+5+7)/3=5。

然后计算权重：a的权重为3/5=0.6，b的权重为5/5=1，c的权重为7/5=1.4。

因此，样本数据a的权重为0.6，样本数据b的权重为1，样本数据c的权重为1.4。

2.几何平均法求权重

1. 对于每个变量，计算其值的几何平均值：GM = (x1 * x2 * ... * xn)^(1/n)，其中x1, x2, ..., xn是变量的值，n是变量个数。
2. 对于每个变量，计算其权重：weight_i = GM_i / (GM_1 + GM_2 + ... + GM_n)，其中GM_i是第i个变量的几何平均值。
3. 将所有变量的权重进行归一化处理，使其和为1

3.特征值法求权重（我将在后面详细解释这一方法）

1. 构建判断矩阵：将各个指标两两进行比较，构建一个n×n的判断矩阵A，其中n为指标的个数。判断矩阵A的每个元素a_ij表示指标i相对于指标j的重要性。

2. 归一化判断矩阵：对判断矩阵A的每一列进行归一化处理，使得每一列的元素之和等于1。得到归一化判断矩阵A'。

3. 求解特征值和特征向量：求解归一化判断矩阵A'的特征值和对应的特征向量。

4. 特征向量归一化：将特征向量进行归一化处理，使得其元素之和等于1。

5. 计算权重：将归一化后的特征向量作为权重，表示各个指标的重要性

2.学习路线

1.问题的提出

你要购置一台笔记本电脑，考虑功能、价格的因素，如何做出决策？

2.解决问题

我们可以先借助网站来查找（如果是建模等比赛就需要去查找文献）

通过购物网站得知笔记本电脑的品牌

由于解题的方便，我们本次只选择五个品牌进行对比（联想，华硕，戴尔，惠普，苹果）

我们将其分成三个层面

目标层、准则层、方案层。

目标层--确定购买的电脑

准则层--处理器、显卡、屏幕分辨率、钱。

方案层--联想、华硕、戴尔、惠普、苹果。

并且只对其中重要的部分进行对比（可以构建出这一权重表格）

所以现在我们就来处理--指标权重。

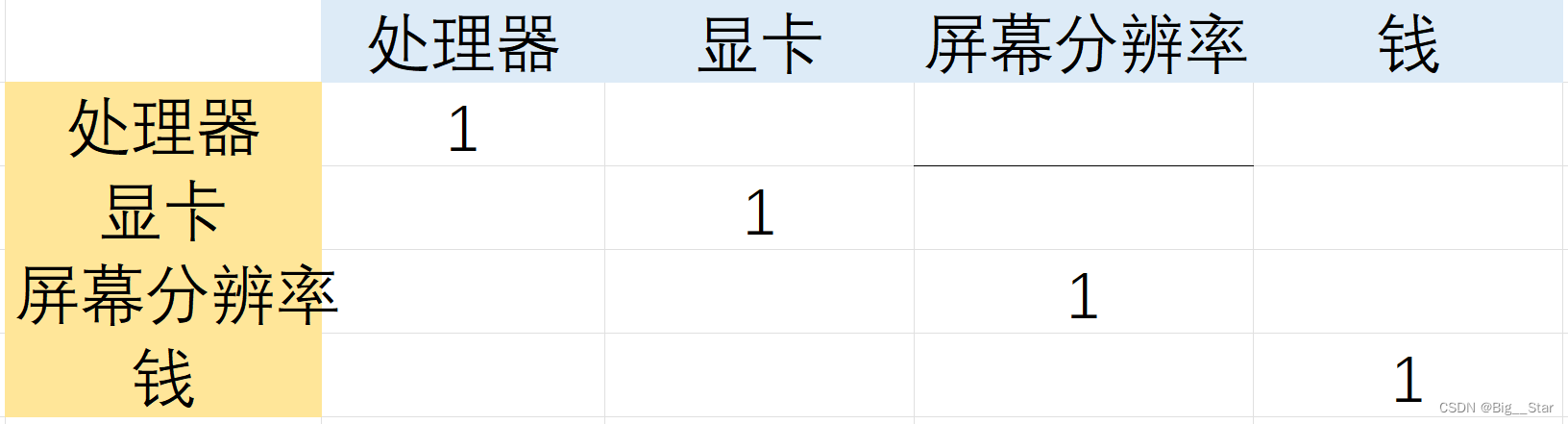
借助比例标度法,令行标为i,列表为j,每一项的值为i/j。（进行填充这一表格）

注意由于每一个人的想法不同，在比赛时，填写这一表需要借助文献和专家！！！

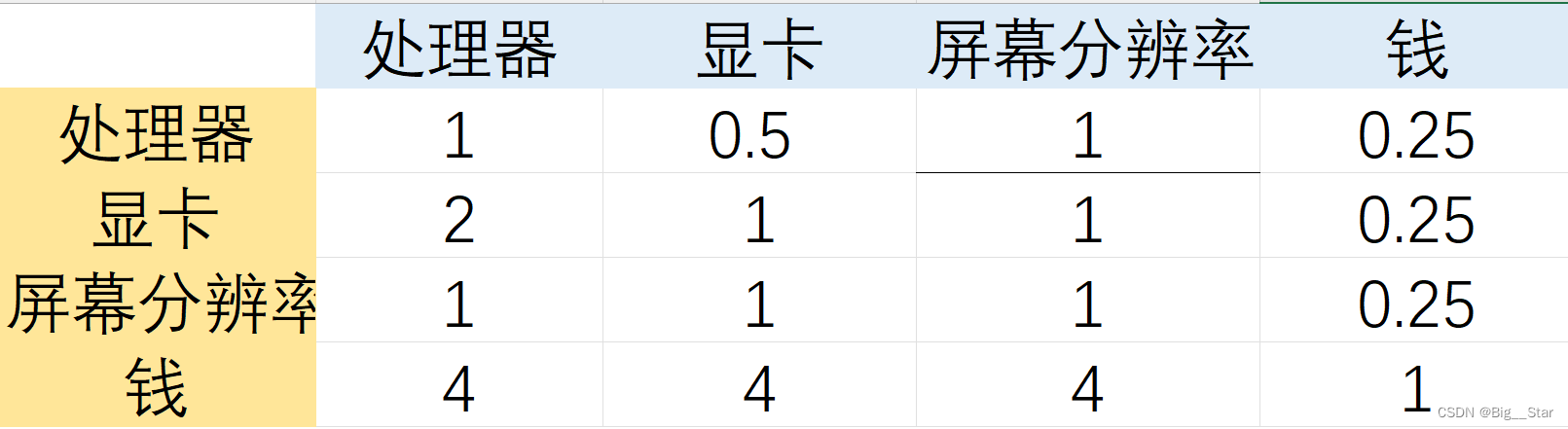
现在我们需要判断每一个电脑对应的方面的权重

等等......

通过填完表计算矩阵求矩阵的时候，必须进行一致性检验！！！

这里是线性代数的知识

接下来基于Matlab的代码

算术平均法、几何平均法、特征向量法求权重和一致性指标。

关注我--下文更新代码和继续的算法。