【现代密码学】笔记4--消息认证码与抗碰撞哈希函数《introduction to modern cryphtography》

写在最前面

主要在 哈工大密码学课程 张宇老师课件 的基础上学习记录笔记。

内容补充：骆婷老师的PPT
《introduction to modern cryphtography》–Jonathan Katz, Yehuda Lindell（现代密码学——原理与协议）中相关章节
密码学复习笔记 这个博主好有意思

初步笔记，如有错误请指正

快速补充一些密码相关的背景知识

---

4 消息认证码与抗碰撞哈希函数

1. 本节学习用于保护信息的完整性和真实性的消息认证码（MAC）和抗碰撞的哈希函数（CRHF）。

2. 目录：MAC、构建安全MAC、CBC-MAC、CRHF、HMAC、信息论上MAC。

3. 完整性与真实性（Integrity and Authentication）

   • 敌手篡改传输中的密文（或明文）是对完整性的攻击；
     敌手伪装成Alice发送密文（或明文）是对真实性（认证）的攻击；
   • 上述两种攻击可以归结为对真实性（认证）的攻击，消息是由敌手构造并发出的；
   • 注意，这里的真实性是指消息的来源是来自接受者所预期的发送者，不是指内容的真假！

MAC

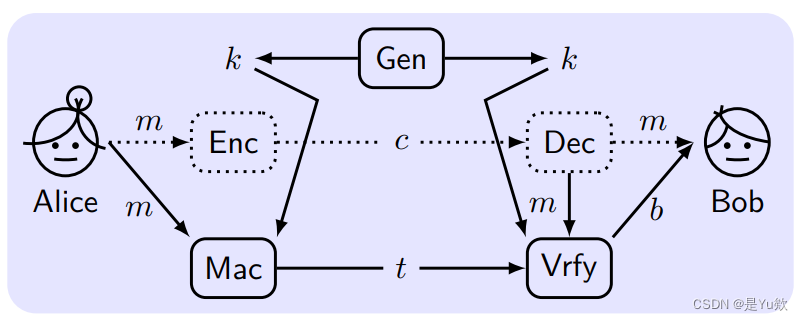
4. MAC的词法（Message Authentication Code）
   

   • 密钥 $k$, 标签(tag) $t$, 一个比特 $b$ 为有效的 (valid}) ，如果 $b=1$;
     或 无效的 ?(invalid}?) ，如果 $b=0$.
   • 密钥生成 Key-generation 算法 $k\leftarrow \mathsf{G}\mathsf{e}\mathsf{n}(1^n),|k|\ge n$.
   • 标签生成 Tag-generation 算法 $t\leftarrow {\mathsf{M}\mathsf{a}\mathsf{c}}_k(m)$.
   • 验证 Verification 算法 $b:={\mathsf{V}\mathsf{r}\mathsf{f}\mathsf{y}}_k(m,t)$.
   • 消息认证码 Message authentication code: $\Pi =(\mathsf{G}\mathsf{e}\mathsf{n},\mathsf{M}\mathsf{a}\mathsf{c},\mathsf{V}\mathsf{r}\mathsf{f}\mathsf{y})$.
   • 基本正确性需求 Basic correctness requirement : ${\mathsf{V}\mathsf{r}\mathsf{f}\mathsf{y}}_k(m,{\mathsf{M}\mathsf{a}\mathsf{c}}_k(m))=1$.
   • 注：不同于加密方案，MAC并不需要从标签得到密文。

5. MAC安全

   • 直觉上，没有敌手能够伪造一个从未被发送过的新消息的有效标签。这里“新消息”是为了排除“重放攻击”。
   • 重放攻击（Replay attack）：敌手记录并发送之前的消息和标签，从而发送了一个伪造的消息并带有有效的标签；为了避免重放攻击，可以通过两种非密码学的方法。
     • 序列号：接收方需要记录之前的序列号，从而发现序列号较小（或曾经接收过的）的旧消息；
     • 时间戳：双方维护时钟同步，从而发现晚与当前时钟的旧消息；
     • 这两种方法都不依赖于密码学，因此，防御重放攻击不需要在密码学的范畴内考虑。
   • 存在性不可伪造（Existential unforgeability）：不能伪造任何消息的标签，一个都不能伪造。
     • 存在性伪造 Existential forgery: 至少伪造一个消息的标签。
     • 选择性伪造 Selective forgery: 实施攻击前选择一个消息，并伪造该消息的标签。
     • 全域性伪造 Universal forgery: 伪造任意给定的消息的标签。
     • 最强的安全目标是阻止最弱的敌手造成的后果。
   • 适应性选择消息攻击（Adaptive chosen-message attack (CMA)）：敌手在攻击过程中始终具有获得任意消息的有效标签的能力，即访问标签生成预言机；

6. 定义MAC安全

   • 消息认证实验 ${\mathsf{M}\mathsf{a}\mathsf{c}\mathsf{f}\mathsf{o}\mathsf{r}\mathsf{g}\mathsf{e}}_{\mathcal{A},\Pi }(n)$ 在挑战者和敌手之间：
     1. 挑战者生成密钥 $k\leftarrow \mathsf{G}\mathsf{e}\mathsf{n}(1^n)$.
     2. 敌手 $\mathcal{A}$ 具有访问标签生成算法${\mathsf{M}\mathsf{a}\mathsf{c}}_k(?)$的预言机的能力，并输出 $(m,t)$. 对预言机查询的消息集合为 $\mathcal{Q}$ 。
     3. ${\mathsf{M}\mathsf{a}\mathsf{c}\mathsf{f}\mathsf{o}\mathsf{r}\mathsf{g}\mathsf{e}}_{\mathcal{A},\Pi }(n)=1?$ ${\mathsf{V}\mathsf{r}\mathsf{f}\mathsf{y}}_k(m,t)=1$ $\wedge$ $m\in /\mathcal{Q}$. 敌手成功，如果输出的消息和标签通过了验证，并且输出的消息是从未向预言机查询过的新消息。
   • 定义：一个 MAC $\Pi$ 是在适应性CMA下的存在性不可伪造 (existentially unforgeable under an adaptive CMA)，如果 $?$ PPT $\mathcal{A}$, $?$ $\mathsf{n}\mathsf{e}\mathsf{g}\mathsf{l}$ 使得: $\mathrm{Pr}[{\mathsf{M}\mathsf{a}\mathsf{c}\mathsf{f}\mathsf{o}\mathsf{r}\mathsf{g}\mathsf{e}}_{\mathcal{A},\Pi }(n)=1]\le \mathsf{n}\mathsf{e}\mathsf{g}\mathsf{l}(n).$
     如果对名称不熟悉，可以参考下方的概念回顾。

概念回顾（是的，我忘记这些缩写是什么了。。）

PPT在密码学中代表“概率多项式时间”（Probabilistic Polynomial Time），这是一种衡量算法或攻击者能力的标准。在这个特定的上下文中，PPT是用来描述攻击者的计算能力。

让我们来详细解释这个定义：

MAC的定义

• MAC：MAC代表“消息认证码”（Message Authentication Code），它是一种用于验证消息完整性和来源真实性的加密工具。
• 存在性不可伪造：一个MAC系统被称为“存在性不可伪造”的，意味着没有攻击者可以成功地伪造一个有效的MAC（即使是一个新的、以前未见过的MAC），除非通过微不足道的概率。

适应性CMA（Chosen Message Attack）

• 适应性CMA：适应性选择消息攻击（Adaptive Chosen Message Attack）是一种攻击模型，其中攻击者可以选择并获得先前消息的MAC值，然后尝试基于这些信息伪造新消息的MAC。
• 存在性不可伪造：在适应性CMA环境下，存在性不可伪造意味着攻击者在选择任意消息并获取其MAC后，仍然无法伪造其他任何消息的MAC。

PPT攻击者

• PPT攻击者：概率多项式时间攻击者是指那些拥有多项式时间计算能力的攻击者。这意味着他们的计算资源是有限的，不能进行无限的尝试或拥有无限的计算能力。
• 重要性：在考虑密码系统的安全性时，通常假设攻击者是PPT的。这是一种现实的假设，因为实际中攻击者的资源是有限的。

不可忽略的概率（negl(n)）

• $\mathsf{n}\mathsf{e}\mathsf{g}\mathsf{l}(n)$：这是一个表示概率的术语，指的是某个函数随着输入大小的增长而增长得极其缓慢，以至于在实际中可以忽略不计。
• 应用：在这个定义中，如果对于所有的PPT攻击者$\mathcal{A}$，伪造MAC的概率 $\mathrm{Pr}[{\mathsf{M}\mathsf{a}\mathsf{c}\mathsf{f}\mathsf{o}\mathsf{r}\mathsf{g}\mathsf{e}}_{\mathcal{A},\Pi }(n)=1]$ 是可忽略的，那么就可以说这个MAC系统在适应性CMA下是存在性不可伪造的。

总结

所以，这个定义的含义是：一个MAC系统在适应性选择消息攻击下被认为是安全的，如果没有任何实际的、有限计算能力的攻击者能够以超过微不足道的概率成功伪造一个MAC。这个标准确保了即使在面对强大但现实的攻击者时，MAC系统也能保持其安全性和完整性。

案例

7. 真实例子

   • WEP 802.11 MAC中的漏洞有两点
   • 一是存在不同消息的CRC32可能是一样的情况，而且这种情况很容易给出。那么，敌手可以查询一个消息$m$并得到对应的标签$t$；然后，输出另一个与所查询消息$m$具有相同CRC32值的新消息$m^{\prime }$，以及查到的标签$t$。
   • 二是敌手可以查询一个消息$m^{\prime }$并获得标签$(r,t^{\prime })$，由此计算得到$F(k,r)=t^{\prime }\oplus \mathsf{C}\mathsf{R}\mathsf{C}32(m^{\prime })$；输出一个新消息$m$以及标签$t=(r,F(k,r)\oplus \mathsf{C}\mathsf{R}\mathsf{C}32(m))$。
   • 上述漏洞展现了攻击MAC的两种常用手段：一是找到两个消息得到相同的中间结果，从而以一个消息的标签作为另一个新消息的标签；二是利用对一个/多个消息的标签来获得构造标签所需的信息，从而构造一个新消息的标签。

8. 例题

   • 如果认为是安全的，则要用反证法证明，若新方案不安全，则原方案也不安全；
   • 如果认为是不安全的，则给出一个新消息和对应的标签；

9. MAC应用

   • Web cookie：Web服务器在发给浏览器的cookie中包含自己生成的MAC标签，来阻止攻击者伪造其他用户的cookie；
   • TCP SYN cookie：在TCP三次握手中，服务器在其发给客户端的初始序列号中包含一个服务器生成的MAC标签，来避免保留握手状态，从而防御SYN Flooding DDoS攻击；
   • 临时一次口令：用户发送给服务器的临时登录口令为一个MAC标签$p={\mathsf{M}\mathsf{a}\mathsf{c}}_k(T)$，其中$k$为原始口令，$T$为当前时间（按半分钟取整）；敌手窃听了之前的临时口令也无法伪造未来的临时口令；

构建安全MAC

10. 构造安全MAC

    • 基于PRF构造安全MAC
      • $F$ 是 PRF. $|m|=n$.
      • $\mathsf{G}\mathsf{e}\mathsf{n}(1^n)$: k ← { 0 , 1 } n k \gets \{0,1\}^n k←{0,1}n .
      • ${\mathsf{M}\mathsf{a}\mathsf{c}}_k(m)$: $t:=F_k(m)$.
      • ${\mathsf{V}\mathsf{r}\mathsf{f}\mathsf{y}}_k(m,t)$: $1?t\stackrel{?}{=}{F}_k(m)$.
    • 定理：如果 $F$ 是一个PRF，那么上述构造是安全的固定长度 MAC。
    • 引理：如果 $F$ 是一个 PRF，那么 $F_k^t(m)=F_k(m)[1,\dots ,t]$ 也是一个PRF。
      • 注：这个引理说明部分输出仍保留伪随机性。引理成立的原因在于，如果根据更短的输出可以区分出伪随机函数，那么根据原长度输出也可以区分出伪随机函数了。

11. 证明基于PRF的安全MAC

    • 证明思路是从PRF的区分器算法$D$规约到伪造标签的敌手算法$\mathcal{A}$。$D$作为$\mathcal{A}$的挑战者，用$D$要区分的预言机作为$\mathcal{A}$的标签生成预言机；当$\mathcal{A}$伪造标签成功时，$D$输出1。

12. 证明基于PRF的安全MAC（续）

    • 如果是真随机 $f$ 被使用 $t=f(m)$ 是均匀随机的.

      $\mathrm{Pr}[D^{f(?)}(1^n)=1]=\mathrm{Pr}[{\mathsf{M}\mathsf{a}\mathsf{c}\mathsf{f}\mathsf{o}\mathsf{r}\mathsf{g}\mathsf{e}}_{\mathcal{A},\tilde{\Pi }}(n)=1]\le 2^{?n}.$

    • 如果 $F_k$ 被使用，那么就是在执行实验 ${\mathsf{M}\mathsf{a}\mathsf{c}\mathsf{f}\mathsf{o}\mathsf{r}\mathsf{g}\mathsf{e}}_{\mathcal{A},\Pi }(n)$.

      $\mathrm{Pr}[D^{F_k(?)}(1^n)=1]=\mathrm{Pr}[{\mathsf{M}\mathsf{a}\mathsf{c}\mathsf{f}\mathsf{o}\mathsf{r}\mathsf{g}\mathsf{e}}_{\mathcal{A},\Pi }(n)=1]=\epsilon (n).$

    • 根据PRF的定义有，$\left|\mathrm{Pr}[D^{F_k(?)}(1^n)=1]?\mathrm{Pr}[D^{f(?)}(1^n)=1]\right|\ge \epsilon (n)?2^{?n}.$

13. 扩展到变长消息

    • 对于变长消息，下面的建议是安全的吗？
    • 建议1：将所有块异或后，对结果进行认证：$t:={\mathsf{M}\mathsf{a}\mathsf{c}}_k^{\prime }({\oplus }_i{m}_i)$；
    • 建议2：对每个块分别认证，$t_i:={\mathsf{M}\mathsf{a}\mathsf{c}}_k^{\prime }(m_i)$；
    • 建议3：对每个块连带一个序列号一起认证， $t_i:={\mathsf{M}\mathsf{a}\mathsf{c}}_k^{\prime }(i\Vert m_i)$.

CBC-MAC

CBC概念回顾

CBC-MAC（Cipher Block Chaining Message Authentication Code）是一种基于块加密算法的消息认证码（MAC）构造方法。它使用的是密码块链接（Cipher Block Chaining，CBC）模式，这是一种常用的块加密操作模式。

构造固定长度的CBC-MAC

14. 构造固定长度的CBC-MAC

    • 为了构造用于变长消息的MAC，先学习固定长度的CBC-MAC，其与CBC结构类似，做了两处改变：
    • 改动1：将初始向量IV改为0；如果不这样改动，则敌手查询 $m_1$ 并获得 $(IV,t_1)$；然后，输出 $m_1^{\prime }=I{V}^{\prime }\oplus IV\oplus m_1$ 并且 $t^{\prime }=(I{V}^{\prime },t_1)$，一个有效的标签。
    • 改动2：标签只包括最后一个块的输出；如果不这样改动，则敌手查询 $m_i$ 并得到 $t_i$；然后，输出 $m_i^{\prime }=t_{i?1}^{\prime }\oplus t_{i?1}\oplus m_i$ 以及 $t_i^{\prime }=t_i$，一个有效的标签。

15. 构造固定长度的CBC-MAC（续）

    • 定理：如果$F$是一个PRF，那么上面的构造就是一个安全的固定长度MAC。
    • 这个构造不能用于变长消息，因为对于一个块的消息$m$和标签$t$，敌手可以在其后添加一个块$m\oplus t$并且输出标签$t$。

16. 安全变长MAC

    • 有三种方法可以将CBC-MAC改造为用于变长消息的MAC，都可以防御上面在结尾添加新块的攻击。
    • 输入长度密钥分离：$k_{?}:=F_k(?)$, 用 $k_{?}$ 作为 CBC-MAC 的密钥。不同长度下采用不同密钥，追加新块后长度变化，之前的标签无法利用。
    • 在开头添加长度：在CBC-MAC的明文$m$前添加一个长度块$|m|$。不同长度下消息有不同的初始块，追加新块后长度变化，之前的标签无法利用。
    • 加密末块输出（ECBC-MAC）：采用两个密钥$k_1,k_2$。用$k_1$和CBC-MAC计算出 $t$，然后输出 $\hat{t}:=F_{k_2}(t)$。输出结果被加密，之前的标签无法利用。

17. MAC填充（Padding）

    • 与加密类似，为了将消息长度与块长度对齐，MAC中也需要在消息中填充。为了安全性，需要保证填充是可逆的，即不同的消息在填充后也应该不同！
    • $m_0=m_1?\mathsf{p}\mathsf{a}\mathsf{d}(m_0)=\mathsf{p}\mathsf{a}\mathsf{d}(m_1).$
    • ISO的填充标准：用“100…00”填充，并按需填充哑块。
    • 如果不填充哑块，则会导致什么？
    • CMAC（Cipher-based MAC）：不填充哑块，不加密最后一块的输出，密钥包括三个 $k,k_1,k_2$
      • $k$用于CBC-MAC；
      • $k_1$ 和 $k_2$ 与最后一块消息异或来阻止利用最后一块输出；
      • 用$k_1$ 和 $k_2$ 来区分是否添加了哑块。

CRHF：哈希函数Hash Function、 定义抗碰撞Collision Resistance

18. 定义哈希函数（Hash Function）

    • 一个哈希函数 (压缩函数) 是一对PPT算法 $(\mathsf{G}\mathsf{e}\mathsf{n},H)$ 满足以下条件:
      • 一个密钥 $s\leftarrow \mathsf{G}\mathsf{e}\mathsf{n}(1^n)$， $s$ 不保密.
      • H s ( x ) ∈ { 0 , 1 } ? ( n ) H^s(x) \in \{0,1\}^{\ell(n)} Hs(x)∈{0,1}?(n)， 其中 x ∈ { 0 , 1 } ? x \in \{0,1\}^* x∈{0,1}? 且 $?$ 为多项式。
    • 若 $H^s$ 只在 x ∈ { 0 , 1 } ? ′ ( n ) x \in \{0,1\}^{\ell'(n)} x∈{0,1}?′(n) 上定义并且 ${?}^{\prime }(n)>?(n)$，那么 $(\mathsf{G}\mathsf{e}\mathsf{n},H)$ 是固定长度的哈希函数。
    • 上面的定义说明，哈希函数将长消息转变为短消息。

19. 定义抗碰撞（Collision Resistance）

    • 碰撞（Collision）：$x=x^{\prime }$ 并且 $H(x)=H(x^{\prime })$。

    • 抗碰撞（Collision Resistance）：对于任意PPT算法，找到碰撞是不可能的。

    • 碰撞发现实验${\mathsf{H}\mathsf{a}\mathsf{s}\mathsf{h}\mathsf{c}\mathsf{o}\mathsf{l}\mathsf{l}}_{\mathcal{A},\Pi }(n)$:

      • $s\leftarrow \mathsf{G}\mathsf{e}\mathsf{n}(1^n)$.

        • 敌手 $\mathcal{A}$ 输入 $s$ ，输出 $x,x^{\prime }$. 注：敌手有$s$，意味着可以访问哈希函数

      • ${\mathsf{H}\mathsf{a}\mathsf{s}\mathsf{h}\mathsf{c}\mathsf{o}\mathsf{l}\mathsf{l}}_{\mathcal{A},\Pi }(n)=1?x=x^{\prime }\wedge H^s(x)=H^s(x^{\prime })$.

      • 哈希函数 $\Pi$ ($\mathsf{G}\mathsf{e}\mathsf{n}$, $H^s$) 是抗碰撞的，如果$?$ ppt $\mathcal{A}$， $?\mathsf{n}\mathsf{e}\mathsf{g}\mathsf{l}$ 使得
        $\mathrm{Pr}[{\mathsf{H}\mathsf{a}\mathsf{s}\mathsf{h}\mathsf{c}\mathsf{o}\mathsf{l}\mathsf{l}}_{\mathcal{A},\Pi }(n)=1]\le \mathsf{n}\mathsf{e}\mathsf{g}\mathsf{l}(n).$

20. 哈希函数安全的更弱的概念

    • 抗碰撞（Collision resistance）: 难以找到 $(x,x^{\prime }),x^{\prime }=x$ 使得 $H(x)=H(x^{\prime })$.
    • 抗二次原像 （Second pre-image resistance）: 给定 $s$ 和 $x$, 难以发现 $x^{\prime }=x$ 使得 $H^s(x^{\prime })=H^s(x)$.
    • 抗原像 （Pre-image resistance）: 给定 $s$ 和 $y=H^s(x)$, 难以发现 $x^{\prime }$ 使得 $H^s(x^{\prime })=y$.
    • 攻击越难，反过来可以防范这种攻击的安全性就越弱。

21. 关于CRHF的问题

    • 如果认为不是，那么请给出一个碰撞；
    • 如果认为是，则用反证法证明找到了$H^{\prime }$的碰撞意味着$H$的碰撞。

22. 哈希函数的应用

    • 文件指纹和去重（Fingerprinting 和 Deduplication）：识别一个文件，用于病毒指纹识别，去重复，P2P文件共享；
    • 默克尔树 （Merkle Tree）：构造多个文件或一个文件多个部分的指纹，从而定位有问题的文件或者文件中的部分；
    • 口令哈希（Password Hashing）：$(salt,H(salt,pw))$，缓解明文口令泄漏风险；
    • 密钥派生（Key Derivation）：从一个高熵（但不必均匀随机）的共享秘密中派生一个密钥；
    • 承诺方案（Commitment Scheme）：将一个承诺与一份信息绑定，隐藏承诺的信息；例如，互联网上掷硬币。

23. 生日问题

    • 生日问题：“如果一群人中有两个人的生日是同一天的概率有1/2，这群人数有多少？”。答案是23。这与我们平时的认知差异，也被称作“生日悖论”。具体计算见教材附件。
      

    • 这个问题意味着哈希函数的输出需要足够长，否则敌手可能通过蛮力枚举来发现碰撞。

    • 在现实攻击中，找到有意义的消息的碰撞对于攻击者来说更有价值。这对攻击者来说并不是难题，可以很容易的构造足够数量的、有意义的消息来实施攻击。对消息中一个单词的替换，所构造明文的数量翻番。

24. MD变换（Merkle-Damga?rd Transform）

    • 从定长哈希函数$(\mathsf{G}\mathsf{e}\mathsf{n},h)$ ($2?$ bits $\to ?$ bits, $?=?(n)$)构造变长哈希函数 CRHF $(\mathsf{G}\mathsf{e}\mathsf{n},H)$ :
      • $\mathsf{G}\mathsf{e}\mathsf{n}$: 不变
      • $H$: 密钥 $s$ 与串 x ∈ { 0 , 1 } ? x \in \{0,1\}^* x∈{0,1}?, $L=|x|<2^{?}$:
        • $B:=?\frac{L}{?}?$ (块数)。 用0填充。 $?$-位的块 $x_1,\dots ,x_B$。最后一块是长度 $x_{B+1}:=L$， $L$ 以 $?$ 位编码，这是必要的，因为只用0填充会导致不同消息的输入是一样的。
        • $z_0:=IV=0^{?}$。 对于 $i=1,\dots ,B+1$， 计算 $z_i:=h^s(z_{i?1}\Vert x_i)$。

25. MD变换的安全性

    • 定理：如果$h$是定长CRHF，那么$H$也是CRHF。
    • 证明：思路是$H$上的碰撞意味着$h$上的碰撞，而$h$是不会被找到碰撞的。两个消息 $x=x^{\prime }$ ，长度分别为 $L$ 和 $L^{\prime }$ ，块数分别为$B$ 和 $B^{\prime }$，使得 $H^s(x)=H^s(x^{\prime })$。 有两种情况：
      • $L=L^{\prime }$: $z_B\Vert L=z_{B^{\prime }}\Vert L^{\prime }$；长度不同，意味着最后一个哈希函数$h$的输入不同，但输出相同，发现碰撞。
      • $L=L^{\prime }$: $z_{i^{?}?1}\Vert x_{i^{?}}=z_{i^{?}?1}^{\prime }\Vert x_{i^{?}}^{\prime }$；长度相同，意味着中间某一块的输入不同，但输出相同，发现碰撞。
      • 因此，必定有 $x=x^{\prime }$ 使得 $h^s(x)=h^s(x^{\prime })$。
    • 作业中有关于MD变换的变体的安全性分析问题。

26. 从分组密码构造CRHF

    • 可以从块密码来构造CRHF，例如Davies-Meyer方法 (SHA-1/2, MD5) $h_i=F_{m_i}(h_{i?1})\oplus h_{i?1}$，或者 Miyaguchi-Preneel 方法 (Whirlpool) $h_i=F_{h_{i?1}}(m_i)\oplus h_{i?1}\oplus m$。
    • 定理：如果$F$是一个理想的加密方案，那么Davies-Meyer构造得到一个CRHF。注：理想的加密方案参考后面要学习的随机预言机模型。目前，没有找到$F$是强伪随机排列下该方法是CRHF的证明。
    • 对于这个定理不做严格证明，而是回答两个问题：
      • 如果 $h_i=F_{m_i}(h_{i?1})$ ，不与 $h_{i?1}$ 异或，会如何？敌手尝试以相同的$h_i$和不同的$m_i$对$F$求逆。
      • 如果 $F$ 不是理想的，而是 $?x,F_k(x)=x$，会如何？敌手输入不同$m_i$，但都得到0；

27. SHA-1和MD5

    • 曾将广泛采用的哈希函数SHA1和MD5都已经被破解。对于128位的MD5，找到碰撞需要$2^{20.96}$；对于160位的SHA1，找到碰撞需要$2^{51}$。

HMAC

28. Hash-and-MAC

    • 有了CRHF，一个自然的想法是：先将任意长度消息哈希，然后通过PRF对哈希值做MAC，实现任意长度消息MAC。$F_k(H(m))$
    • 这个方案的安全性分两种情况分析：当不同消息得到相同哈希值时，这意味着碰撞发生；否则，意味着MAC标签被伪造。

29. NMAC

    • 使用CRHF（MD变换）来构造MAC，而不需要用PRF
    • 之所以需要开头的密钥，是为了在哈希函数为弱抗碰撞性时也保障安全；如果哈希函数是CRHF，则不需要开头的密钥
    • 缺点：需要修改哈希函数（MD变换中初始向量）

30. HMAC（基于哈希的MAC）

    • 以MD变换为基础构造一个安全的MAC。在开头和结尾以两个不同密钥作为哈希函数输入。
    • 不需要修改哈希函数。
    • $\mathsf{G}\mathsf{e}\mathsf{n}(1^n)$: 输出 $(s,k)$. s ← G e n ~ , k ← { 0 , 1 } n s \gets \widetilde{\mathsf{Gen}}, k \gets \{0,1\}^n s←Gen ,k←{0,1}n u.a.r；
    • ${\mathsf{M}\mathsf{a}\mathsf{c}}_{s,k}(m)$: $t:=H_{IV}^s((k\oplus \mathsf{o}\mathsf{p}\mathsf{a}\mathsf{d})\Vert H_{IV}^s((k\oplus \mathsf{i}\mathsf{p}\mathsf{a}\mathsf{d})\Vert m\left)\right)$
    • ${\mathsf{V}\mathsf{r}\mathsf{f}\mathsf{y}}_{s,k}(m,t)$: $1?t\stackrel{?}{=}{\mathsf{M}\mathsf{a}\mathsf{c}}_{s,k}(m)$

31. HMAC安全性

    • 定理：$G(k)\stackrel{\text{def}}{=}{h}^s(IV\Vert (k\oplus \mathsf{o}\mathsf{p}\mathsf{a}\mathsf{d}))\Vert h^s(IV\Vert (k\oplus \mathsf{i}\mathsf{p}\mathsf{a}\mathsf{d}))=k_1\Vert k_2$ 。其中，$h$是CRHF。如果$G$是PRG，那么HMAC是安全的。
    • 在HMAC之前，其他不安全的方案包括：
    • $H^s(k\Vert x)$ 存在长度扩展攻击弱点。 在获得$H^s(k\Vert x)$和消息长度后，敌手能够获得新消息 $x\Vert x^{\prime }$ 的有效标签 $H^s(k\Vert x\Vert x^{\prime })$ 。因为$H^s(k\Vert x)$的输出标签$t$和$x^{\prime }$作为哈希函数的输入直接得到输出。
    • $H^s(x\Vert k)$: 在一个弱哈希函数上的碰撞会导致MAC上碰撞。回顾NMAC中需要开头的密钥来支持弱抗碰撞的情况。
    • $H^s(k\Vert x\Vert k)$: 也存在一些已知的弱点，即使使用两个不同的密钥。
    • $H^s(k\Vert H^s(k\Vert x))$：这是NMAC和HMAC的情况

32. HMAC结语

    • HMAC是基于NMAC的改进，是工业标准（RFC2104），HMAC比CBC-MAC更快；

    • 验证计时攻击：

      • Keyczar密码学库（Python）：

      • def Verify(key, msg, sig_bytes):

        \qquad return HMAC(key, msg) == sig_bytes

      • 存在问题是上述比较是按字节匹配，通过观察函数返回时间可以判断相同字节的数量，从而按字节猜测标签内容。

      • 在Xbox 360中，相邻字节上被验证拒绝的时间差有2.2毫秒.

    • 不要自己实现密码学！

信息论上MAC

33. 信息论上MAC安全定义

    • 不可能达到“完美的、不可伪造的”MAC，因为算力无限制的敌手可以至少以$1/2^{|t|}$ 的概率输出一个有效的标签。为此，对敌手查询MAC预言机的次数需要加以限制，下面分析只允许敌手查询一次MAC预言机的情况。
    • 一次消息认证实验 ${\mathsf{M}\mathsf{a}\mathsf{c}\mathsf{f}\mathsf{o}\mathsf{r}\mathsf{g}\mathsf{e}}_{\mathcal{A},\Pi }^{1?\mathsf{t}\mathsf{i}\mathsf{m}\mathsf{e}}$: 敌手查询一次MAC预言机后输出消息和标签，
      • $k\leftarrow \mathsf{G}\mathsf{e}\mathsf{n}$.
      • $\mathcal{A}$ 输出一个消息 $m^{\prime }$并且获得一个标签 $t^{\prime }\leftarrow {\mathsf{M}\mathsf{a}\mathsf{c}}_k(m^{\prime })$, 然后输出 $(m,t)$.
      • ${\mathsf{M}\mathsf{a}\mathsf{c}\mathsf{f}\mathsf{o}\mathsf{r}\mathsf{g}\mathsf{e}}_{\mathcal{A},\Pi }^{1?\mathsf{t}\mathsf{i}\mathsf{m}\mathsf{e}}=1?$ ${\mathsf{V}\mathsf{r}\mathsf{f}\mathsf{y}}_k(m,t)=1$ $\wedge$ $m=m^{\prime }$.
    • 定义：一个MAC $\Pi$ 是一次$\epsilon$-安全的（one-time $\epsilon$-secure），如果 $?$ ppt $\mathcal{A}$: $\mathrm{Pr}[{\mathsf{M}\mathsf{a}\mathsf{c}\mathsf{f}\mathsf{o}\mathsf{r}\mathsf{g}\mathsf{e}}_{\mathcal{A},\Pi }^{1?\mathsf{t}\mathsf{i}\mathsf{m}\mathsf{e}}=1]\le \epsilon .$
    • 这里$\epsilon$应该为$1/2^{|t|}$，才能达到之前的信息论安全。信息论安全的MAC在允许敌手查询MAC预言机若干次之后，成功伪造MAC的概率应该不大于$1/2^{|t|}$。

34. 理解信息论MAC安全

    • 假设敌手算法是确定性的，其最合理的步骤如下：
      • （1）选择的$m^{\prime }$是固定的，查询得到$t^{\prime }$；
      • （2）根据$m^{\prime }$和$t^{\prime }$确定$k$的所有可能集合$\mathcal{K}(t^{\prime })$，从中选择一个$k^{?}$；
      • （3）选择输出$m$是固定的，根据$k^{?}$计算$t$并输出。
    • 问题：$\mathcal{K}(t^{\prime })$太大或太小会如何？
    • 设想如果根据第一次消息和标签能够唯一确定密钥$k$，那么敌手一定可以成功伪造；反之，如果不能唯一确定密钥，并且密钥可能的范围$\mathcal{K}(t^{\prime })$充分大，那么敌手就难以成功伪造。从另一个角度，需要第一次查询获得的一个对消息和标签与敌手伪造另一个新消息的标签这两个事件之间是充分独立的。密钥空间太大也不安全，因为令$(m,t)$是有效标签密钥集合也更大，其概率也增大。

35. 信息论上MAC的构造

    • 一个函数 $h$: $\mathcal{K}\times \mathcal{M}\to \mathcal{T}$ 是一个强全域函数（Strongly Universal Function (SUF)），如果对于所有不同的 $m,m^{\prime }\in \mathcal{M}$ 以及所有 $t,t^{\prime }\in \mathcal{T}$, 以下成立: $\mathrm{Pr}[h_k(m)=t\wedge h_k(m^{\prime })=t^{\prime }]=1/|\mathcal{T}{|}^2$，其中概率来自均匀选择的 $k\in \mathcal{K}$.
    • 为了实现一次$1/2^{|t|}$-安全的MAC，需要一个新的数学对象，不同输入会独立产生不同的输出，输入间任何差异都会导致输出之间是完全独立的。将函数的这种性质称为：“成对独立的，pairwise-independent” 或者 “成对不可预测，pairwise-unpredictable”。
    • SUF是具有上面性质的函数，下一页证明
    • 信息论安全MAC构造：
      • 令 $h$: $\mathcal{K}\times \mathcal{M}\to \mathcal{T}$ 为一个SUF.
      • $\mathsf{G}\mathsf{e}\mathsf{n}$: k ← { 0 , 1 } n k \gets \{0,1\}^n k←{0,1}n u.a.r.
      • ${\mathsf{M}\mathsf{a}\mathsf{c}}_k(m)$: $t:=h_k(m)$.
      • ${\mathsf{V}\mathsf{r}\mathsf{f}\mathsf{y}}_k(m,t)$: $1?t\stackrel{?}{=}{h}_k(m)$. (如果 $m\in /\mathcal{M}$，那么输出 0.)

36. 构造一个SUF

    • 定理：对于任意质数 $P$，函数 $h$ 是一个SUF: $h_{a,b}(m)\stackrel{\mathsf{d}\mathsf{e}\mathsf{f}}{=}[a?m+b\mathrm{m}\mathrm{o}\mathrm{d}p]$
    • 证明：$h_{a,b}(m)=t$ 且 $h_{a,b}(m^{\prime })=t^{\prime }$，只有当 $a?m+b=t\mathrm{m}\mathrm{o}\mathrm{d}p$ 且 $a?m^{\prime }+b=t^{\prime }\mathrm{m}\mathrm{o}\mathrm{d}p$. 我们有 $a=[(t?t^{\prime })?(m?m^{\prime }{)}^{?1}\mathrm{m}\mathrm{o}\mathrm{d}p]$ 且 $b=[t?a?m\mathrm{m}\mathrm{o}\mathrm{d}p]$，这意味着存在一个唯一的密钥 $(a,b)$。由于存在 $|\mathcal{T}{|}^2$ 个密钥，$\mathrm{Pr}[h_k(m)=t\wedge h_k(m^{\prime })=t^{\prime }]=\frac{1}{|\mathcal{T}{|}^2}$。

37. 来自SUF的MAC的安全性

    • 定理：如果 $h$ 是一个 SUF，构造是一个 $1/|\mathcal{T}|?$安全MAC.
    • 证明：假设敌手算法是确定性的，不失一般性可以固定$m^{\prime }$并遍历所有可能的$t^{\prime }$，敌手以$(m^{\prime },t^{\prime })$作为输入并输出$(m,t)$。根据SUF的定义，可以得到敌手成功的概率为$1/|\mathcal{T}|$。

38. 信息论MAC的局限性

    • 任意 $?$次 $2^{?n}$-安全 MAC 需要密钥长度至少为 $(?+1)?n$.
    • 定理：令 $\Pi$ 为一次 $2^{?n}$-安全 MAC，其中所有密钥长度相同。那么，密钥必须具有$2n$长度。
    • 证明：直觉上，每对消息和标签成立需要$2^n$个密钥，才能保证 $2^{?n}$-安全。一共2对，需要$2^{2n}$。
    • 令 K ( t ′ ) = d e f { k ∣ V r f y k ( m ′ , t ′ ) = 1 } \mathcal{K}(t') \overset{\mathsf{def}}{=} \{ k | \mathsf{Vrfy}_k(m', t') = 1\} K(t′)=def{k∣Vrfyk?(m′,t′)=1}，即所有由所查询消息得到标签的密钥集合。对于任意 $t^{\prime }$， $|\mathcal{K}(t^{\prime })|\le 2^{?n}?|\mathcal{K}|$。 否则，敌手$\mathcal{A}$从全体密钥集合中随机挑选一个密钥得到 $(m,t)$ 是一个有效标签的概率至少为 $|\mathcal{K}(t^{\prime })|/|\mathcal{K}|>2^{?n}$，这与安全要求矛盾。 $\mathcal{A}$有无限算力可以根据从第一次查询中得到对应的密钥集合$\mathcal{K}(t^{\prime })$，从中选择一个密钥$k^{?}$，并输出一个新消息$m$的有效标签的概率是至少 $\frac{1}{|\mathcal{K}(t^{\prime })|}$。固定$m^{\prime }$遍历所有标签$t^{\prime }$计算敌手成功概率为： ${\sum }_{t^{\prime }}\mathrm{Pr}[{\mathsf{M}\mathsf{a}\mathsf{c}}_k(m^{\prime })=t^{\prime }]?\frac{1}{|\mathcal{K}(t^{\prime })|}\ge {\sum }_{t^{\prime }}\mathrm{Pr}[{\mathsf{M}\mathsf{a}\mathsf{c}}_k(m^{\prime })=t^{\prime }]?\frac{2^n}{|\mathcal{K}|}=\frac{2^n}{|\mathcal{K}|}$ 。由于概率至多 $2^{?n}$, $|\mathcal{K}|\ge 2^{2n}$。由于所有密钥具有相同长度，每个密钥的长度至少是 $2n$。

39. 总结

    • 认证意味着存在不可伪造
    • 用PRF来实现安全MAC
    • 用带密钥的CRHF来实现安全MAC
    • 信息论MAC安全需要非常、非常长的密钥