数据结构 | 手写堆

今天我们来实现一个简单好用的数据结构，堆。

要实现一个手写堆，需要实现它的三个功能，我们需要能初始化一个堆，能取出堆顶元素和将一个元素插入堆。

在开始实现之前，我们先回顾一下堆的初始化、插入和删除过程。

堆的定义

① 堆中的每个结点最多有两个子节点。

②?结点的排列顺序垂直从上到下，水平从左到右。

③?子节点key必须大于父母结点。

堆的数据结构

根据堆的定义，堆是一棵完全二叉树，既然是一棵完全二叉树，就可以采用数组的方式实现，并且，如果从1开始对结点编号，那么，编号为i的结点的父亲结点为i/2。

堆的初始化

堆的初始化过程从倒数第二排开始，遍历检查从n/2结点到1结点的合法性，如图所示，我们计划实现一个小根堆，那么它的初始化过程可以表示为（图像第四步 6和4 不合法，制图失误，抱歉）：

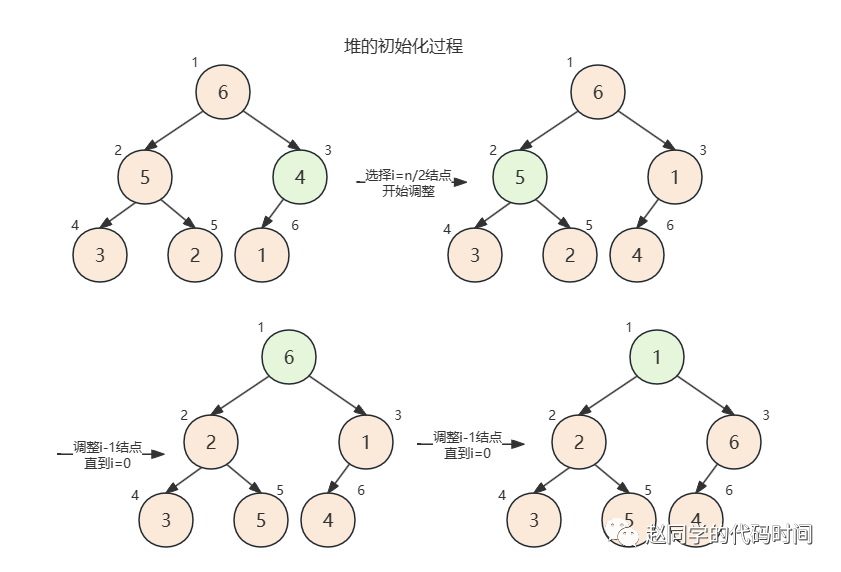
每一次不合法时的调整过程是将该节点与左右孩子中更小的一个互换。

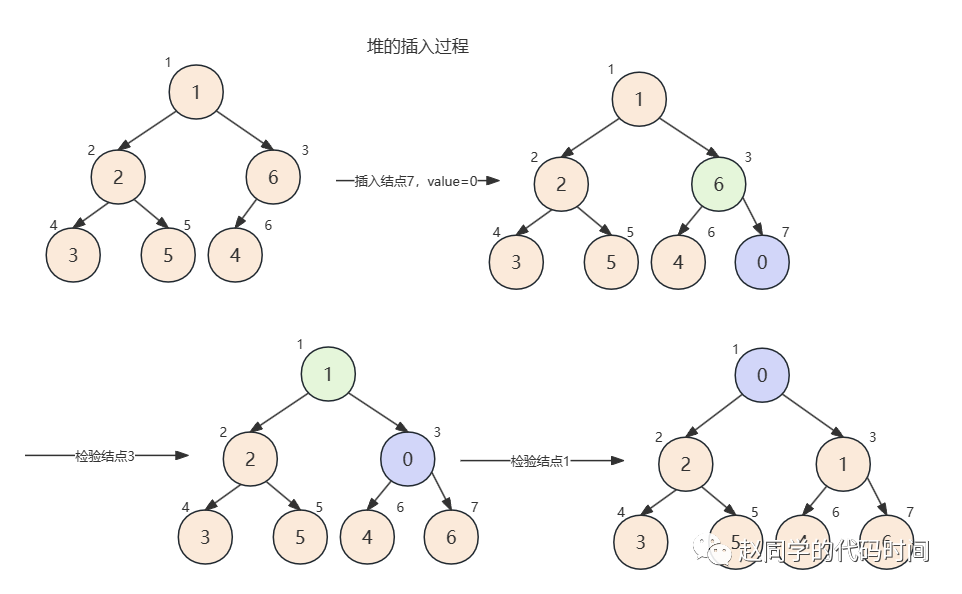
堆的插入

堆的插入过程也是类似的，与初始化过程的差异就是，只需要针对可能受影响的结点做合法性调整即可。

堆的删除

我们要取出堆顶元素，就会打破树的完全二叉树性质，因此，我们得把最后一个元素放到堆顶，然后从堆顶开始向下调整。

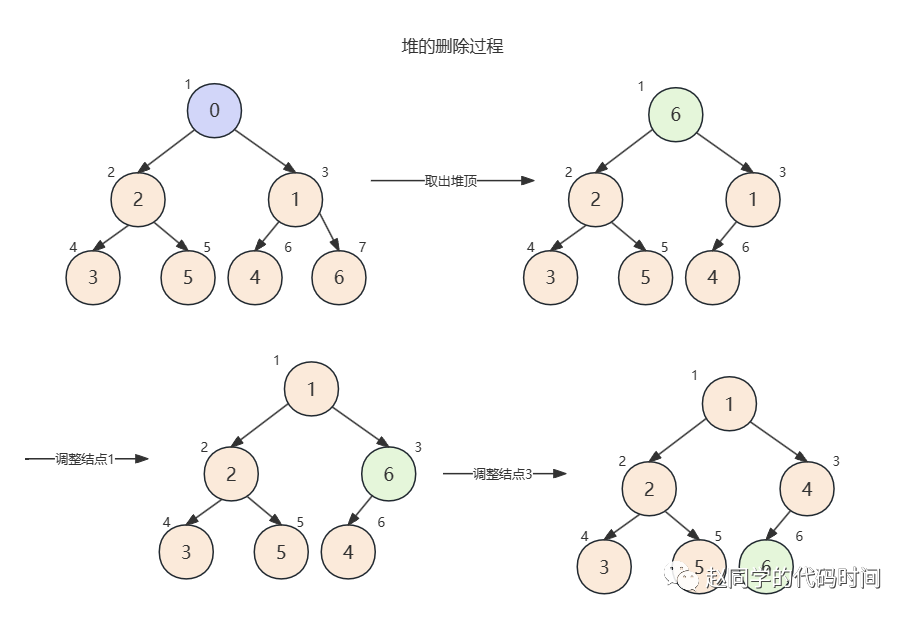
堆排序

堆排序则是将堆元素插入或初始化后，不断取出，从而获得一个有序结果的排序方法。如上图删除过程，实际上是将第一个结点与第七个结点互换，并使得堆大小减一，这样，当堆大小为0时，原来存放堆的数组就是一个有序数组。

实现手写堆的关键

通过分析上述过程，实际上要实现一个手写堆，只需要实现两个函数，一个函数自下而上(up)的检查某个点合法性，用于插入操作，一个函数自上而下(down)的检查某个点合法性，用于删除操作。实现了这两个函数后，就可以轻松地实现插入和删除操作。

#include <iostream>


using namespace std;


#define MAX_NR 100005
int heap[MAX_NR];   // 存放堆的数组
int heap_size;           // 堆大小


// 从上到下调整堆
void down_heap(int idx){
    int t = idx;    //t存储三个结点中存在的最小的结点的下标，初始化为当前结点idx
    if (idx * 2 <= heap_size && heap[idx * 2] < heap[t]) t = idx * 2;     // 左子节点存在并且小于当前结点，更新t的下标
    if (idx * 2 + 1 <= heap_size && heap[idx * 2 + 1] < heap[t]) t = idx * 2 + 1; //右子节点存在并且小于当前结点，更新t的下标
    if (t != idx) //如果t==idx意味着不用变动，idx就是三个结点中拥有最小值的结点下标，否则交换数值
    {
        swap(heap[t], heap[idx]);
        down_heap(t); //交换数值后，t这个结点存储原本u的值，u存储存储t的值（三个数中的最小值）。u不用调整了，但t情况不明，可能需要调整。直到它比左右子节点都小
    }
}


// 从下到上调整堆
void up_heap(int idx){
    idx >>= 1;
    if (!idx) return;
    int t = idx;    //t存储三个结点中存在的最小的结点的下标，初始化为当前结点idx
    if (idx * 2 <= heap_size && heap[idx * 2] < heap[t]) t = idx * 2;     // 左子节点存在并且小于当前结点，更新t的下标
    if (idx * 2 + 1 <= heap_size && heap[idx * 2 + 1] < heap[t]) t = idx * 2 + 1; //右子节点存在并且小于当前结点，更新t的下标
    if (t != idx) //如果t==idx意味着不用变动，idx就是三个结点中拥有最小值的结点下标，否则交换数值
    {
        swap(heap[t], heap[idx]);
        up_heap(idx); //交换数值后，idx这个结点可能需要继续向上调整
    }
}


void init_heap(){
    for(int i = heap_size/2; i; i --){
        down_heap(i);
    }
}


void insert_heap(int data_value){
    heap[++heap_size] = data_value;
    up_heap(heap_size);
}


int pop_heap(){
    int ret = heap[1];
    swap(heap[1], heap[heap_size]);
    heap_size --;
    down_heap(1);
    return ret;
}